§ 4. Методы решения задач линейного программирования

Существует довольно много методов решения задач линейного программирования. Мы коснемся наиболее распространенных из этих методов и по возможности покажем границы их применимости. В данном параграфе описываются простейшие методы, пригодные в основном для решения задач с небольшим числом переменных. Однако, несмотря на простоту и наглядность, эти методы содержат в себе элементы подхода к решению класса задач, значительно более сложных, выходящих за пределы предположений, используемых в линейном программировании.

1. Графический метод. Если было указано, что в тех случаях, когда множество планов задачи линейного программирования образует выпуклый многогранник, линейная функция цели достигает своего оптимального значения в одной из вершин этого многогранника. Это свойство множества планов будет использовано для решения задачи линейного программирования.

Начнем с простого примера, представленного графически на рис. 1.2. Предположим, что в пространстве двух измерений (x₁, x₂) даны выпуклый многоугольник ABCDE, внутренняя область которого является множеством планов задачи, и линейная функция пели f = c₁x₁ + c₂x₂, где c₁>0, c₂>0. Пусть сначала f = 0. При этом прямая c₁x₁ + c₂x₂ = 0 проходит через начало координат. В данном случае точка x₁ = 0, x₂ = 0 не принадлежит многоугольнику решений. Для того чтобы функция f стала соответствовать допустимым решениям задачи, необходимо добиться пересечения прямой f = c₁x₁ + c₂x₂ = const с многоугольником ABCDE. Будем придавать f все увеличивающиеся положительные значения. При этом прямая будет передвигаться вправо, оставаясь параллельной самой себе.

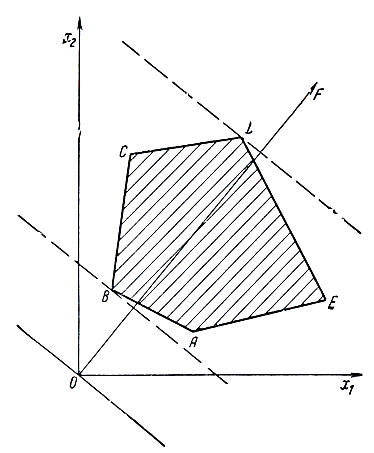
Рис. 1.2

Действительно, можно записать уравнение прямой в виде x₂ = - ^c₁/_c2x₁ + ^f/_c2. Из аналитической геометрии известно, что величина - ^c₁/_c2 определяет угол наклона этой прямой к осям координат. При изменении f этот угол не меняется и прямая передвигается параллельно самой себе в направлении перпендикуляра OF.

Перемещая таким образом прямую f = c₁x₁ + c₂x₂ = const, мы впервые встречаем многоугольник ARCDE в вершине В, где эта прямая становится опорной прямой. Поскольку вершина В находится ближе всего к точке О, она имеет наименьшие координаты (x₁, x₂) и, следовательно, функция f достигает в вершине В наименьшего значения. Перемещая прямую далее, мы, наконец, приходим в вершину D, которая является наиболее удаленной от начала координат точкой многоугольника ABCDE. В этой вершине, очевидно, функция цели f достигает наибольшего значения.

Иногда может случиться, что прямая f = c₁x₁ + c₂x₂ = 0 окажется параллельной одной из сторон выпуклого многоугольника. Тогда линейная функция f = c₁x₁ + c₂x₂ достигает своего наименьшего или наибольшего значения в любой точке, принадлежащей этой стороне. Но и в этом случае функция f достигает этих значений в вершинах, лежащих на этой стороне.

Имеется полная аналогия вышеизложенному при решении задач в пространстве трех измерений. Если заданы многогранник решений в пространстве трех измерение АВСО (рис. 1.3) и линейная функция цели f = c₁x₁ + c₂x₂ + c₃x₃, то проводя плоскость c₁x₁ + c₂x₂ + c₃x₃ = 0 через начало координат и передвигая ее параллельно самой себе (в направлении перпендикуляра, восстановленного к этой плоскости) до встречи с ближайшей к началу координат вершиной многогранника, находим минимальное значение функции цели (на рис. 1.3 вершина О уже дает минимум f). Наиболее удаленная от начала координат вершина A, очевидно, определяет наибольшее значение функции f. На рис. 1.3 пунктиром обозначены линии обозначены линии пересечения плоскости f = const с плоскостями (x₁, x₂), (x₁, x₃), (x₂, x₃).

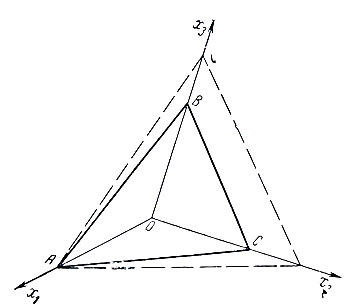
Рис. 1.3

Напомним, что при решении экономических задач интересуются в основном неотрицательными решениями, т. е. из всех возможных решений считаются допустимыми лишь решения x₁≥0, x₂≥0, ..., x_n≥0. Очевидно, что все решения задачи, иллюстрированной рис. 1.2, удовлетворяют этому требованию, поскольку многоугольник ABCDE целиком расположен в первом квадранте системы координат (x₁, x₂). В этом случае требования x₁≥0, x₂≥0 удовлетворяются автоматически и фактически не являются ограничениями. Однако для примера (рис. 1.3) требования x₁≥0, x₂≥0, x₃≥0 явным образом входят в формулировку задачи, являясь ограничениями, определяющими положение трех из четырех граней многогранника. Поэтому об ограничениях вида x_i≥0 всегда следует помнить при решении экономических задач линейного программирования.

Для задач, заданных в пространстве трех измерений, на плоском чертеже зачастую трудно графически отобразить положение многогранника решений и представить взаимное положение этого многогранника и плоскости, определяющей целевую функцию. Поэтому графическое решение тих задач часто оказывается затруднительным.

Графическое решение задач в случае n переменных для n>3 практически не может быть получено, учитывая то обстоятельство, что n-мерное пространство (n>3) является абстрактным математическим понятием.

Таким образом, можно считать, что графический метод , решения задач линейного программирования пригоден в основном для решения задач, заданных в пространстве двух или трех измерений.

2. Алгебраические методы. Поскольку с самого начала основная задача линейного программирования была сформулирована в виде системы m линейных уравнений с n неизвестными, то естественно обратить основное внимание на алгебраические методы решения задачи. При этом описанная выше в § 3 геометрическая интерпретация будет являться фактором, обеспечивающим ориентацию в направлении наиболее быстрого получения решения.

Предварительно кратко, без доказательств, напомним некоторые сведения из линейной алгебры.

Рассмотрим систему n линейных уравнений с n неизвестными:

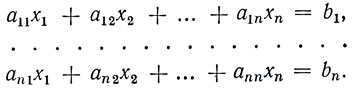
Величина, составленная из коэффициентов a₁₁, ..., a_nn этой системы и записанная следующим образом:

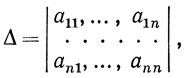
называется определителем системы n-го порядка. Такая формальная запись подразумевает существование некоторого правила для вычисления Δ. Согласно этому правилу определитель n-го порядка представляет из себя алгебраическую сумму n! = 1*2*3*...*n слагаемых вида a_1,i1*a_2,i2...a_n,in, состоящих из n сомножителей, взятых по одному из каждой строки и каждого столбца. В том случае, если слагаемые, у которых вторые индексы сомножителей i₁, i₂, ..., i_n образуют так называемую четную перестановку, берется знак (+), если перестановка нечетная, то знак (-).

Перестановка из n чисел (индексов) называется четной, если число нарушений принятого порядка следования чисел в ней (число инверсий) четно, и нечетной, если число этих нарушений нечетно. Например, числа 1, 2, 3, 4, 5, записанные в принятом порядке возрастания, образуют перестановку. Меняя порядок расположения этих цифр, получим другие перестановки: (1, 3, 2, 4, 5), (1, 2, 4, 3, 5) и т. д. Всего может быть 5! = 120 перестановок из пяти элементов. Из n различных элементов можно составить n! перестановок. Нарушение принятого порядка следования чисел, таким образом, имеется у всех, кроме одной, перестановок.

Сформулированное выше правило вычисления определителя я-го порядка можно записать в виде

где t - число инверсий в перестановке (i₁, i₂, ..., i_n).

В качестве примера выпишем определитель третьего порядка, состоящий из 3! = 6 чисел:

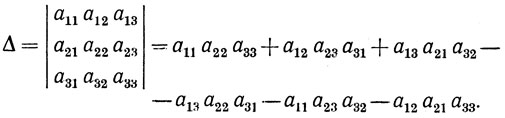
Можно легко проверить справедливость общей формулы на примере этого определителя. Вычисление определителей более высокого порядка также не представляет трудностей, хотя объем вычислений при этом сильно возрастает.

Если теперь в определителе системы Δ заменить j-й столбец столбцом свободных членов, то получим определитель

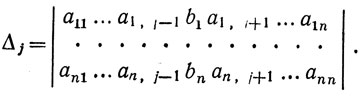
В том случае, если определитель системы Δ≠0, система из n уравнений с n неизвестными имеет единственное решение, определяемое равенствами

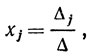
(j = 1, 2, ..., n)

В том случае, если Δ = 0, система является либо несовместной, либо имеет бесконечное множество решений.

Перейдем теперь к наиболее общему случаю системы m линейных уравнений с n неизвестными (система вида (1.1)):

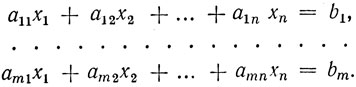
Прямоугольная таблица, составленная из коэффициентов этой системы

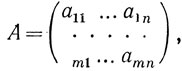
называется матрицей системы. Матрица в частном случае может состоять из одной строки (матрица-строка) или из одного столбца (матрица-столбец).

Если в матрице А переставить строки со столбцами, то получим новую матрицу

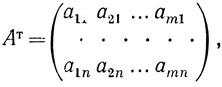
которая называется транспонированной матрицей по отношению к A. Соответственно и матрица А является транспонированной по отношению к A^т.

Пусть для определенности в матрице Am≤. Из элементов этой матрицы, сохраняя порядок, в котором расположены ее элементы, можно образовать определители второго, третьего и т. д. до m-го порядков. Может случиться, что определители m-го, (m-1)-го и т. д. до (r+1)-го порядков включительно равны нулю, но хотя бы один определитель r-го порядка отличен от нуля. Тогда число r называется рангом матрицы А. Понятие ранга матрицы является весьма важным для линейного программирования. Укажем элементарные преобразования матриц, которые не меняют ее ранга:

1. вычеркивание из матрицы строки или столбца, состоящих из одних нулей;
2. умножение элементов строки или столбца на любое число (кроме нуля);
3. перестановка двух строк (или столбцов);
4. сложение элементов одной строки (или столбца) и соответствующих элементов другой строки (или столбца), умноженных на одно и то же число.

Матрица А и транспонированная к ней матрица А^Т имеют один и тот же ранг.

Рассмотрим теперь две матрицы: одну, составленную из коэффициентов записанной выше системы уравнений

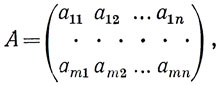
и другую, в которую введен столбец свободных членов этой системы

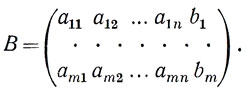
Матрица В называется расширенной по отношению к матрице А.

Система из m уравнений с n неизвестными совместна (т. е. существует хотя бы одна совокупность значений переменных x₁* ... x*_n, тождественно удовлетворяющих всем уравнениям системы) тогда и только тогда, когда ранг матрицы А равен рангу расширенной матрицы В. В том случае, когда ранг обеих матриц равен числу неизвестных, т. е. r = n, система имеет единственное решение. Если r<n, система имеет бесконечное множество решений. Это означает, что имеется область допустимых решений системы. И обратно, если ранг матриц А и В не совпадает, то система несовместна и не имеет ни одного решения.

При решении экономических задач линейного программирования приходится иметь дело в основном с совместными системами уравнений, у которых ранг матриц А и В меньше числа переменных n. Смысл решения этих задач состоит в отыскании среди бесконечного множества решений такого, которое обращает в максимум или минимум функцию цели. Как мы уже знаем из геометрической интерпретации задач линейного программирования, искомые максимум или минимум достигаются в экстремальных точках области допустимых решений системы. Поэтому при алгебраическом решении задачи необходимо сформулировать алгоритм, с помощью которого путем тождественных алгебраических преобразований можно было бы найти координаты экстремальных точек и выбрать из них ту, которая обеспечивает оптимальное решение.

Такой алгебраический метод решения задач линейного программирования разработан и называется методом последовательного улучшения плана, или симплексным методом (название носит сугубо исторический характер). Геометрически этот метод представляет переход от одной вершины выпуклого многогранника к соседней (лежащей на одной грани с данной вершиной), от нее к следующей и т. д. Решение системы, являющееся экстремальной точкой или вершиной многогранника решений, называется базисным решением, или просто базисом. Переходу от вершины к вершине соответствует переход от одного базиса к другому.

В случае малого количества переменных (двух-трех) могут быть получены простые алгебраические решения без применения симплекс-метода, так как экстремальные точки сравнительно просто определяются из совместного решения систем уравнения, на которые может быть разложена исходная система задачи. При наличии большого числа переменных простой алгебраический подход становится мало пригодным из-за возрастающей сложности вычислений. Смысл симплексного метода состоит в том, что предлагается процедура нахождения базисных решений и среди них оптимального решения, исключающая необходимость решения систем уравнений.

Ввиду важности симплексного метода для решения экономических задач подробному описанию этого метода посвящается отдельный параграф.