§ 3. Геометрическая интерпретация задачи линейного программирования

1. Множество. В математике используется самое общее понятие множества. Нас конкретно будут интересовать множества точек различных геометрических фигур: прямых, треугольников, многоугольников, многогранников и т. д. Множество считается заданным, если указано свойство, которым обладают все его элементы и благодаря которому эти элементы отличаются от всех объектов, не принадлежащих данному множеству. Тот факт, что х является элементом множества М, обозначается следующим образом: х∈М. Специальным классом множеств являются выпуклые множества.

2. Выпуклые множества. Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и весь отрезок, соединяющий эти точки.

Простейшим примером выпуклого множества является отрезок AB, соединяющий точки А и В (рис. 1.1). Пусть концы этого отрезка в некоторой прямоугольной системе координат (x₁, x₂) имеют координаты А (x₁', x'₂), в (x"₁, x"₂) (рис. 1.1.)

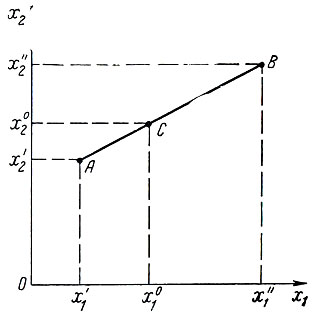
Рис. 1.1

Пусть точка С (x°₁, х°₂) делит отрезок А В па две части в отношении μ. Выразим координаты точки С через координаты точек А и В.

Для этого спроектируем сначала точки A, В, С на ось 0x₁. На основании известной теоремы геометрии имеем 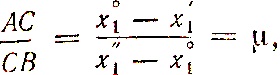откуда находим 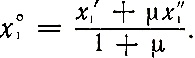Точно так же 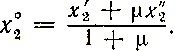Обозначим ¹/_1+μ = λ и преобразуем эти формулы к виду

где λ может принимать значения 0≤λ≤1.

Можно ввести иную формальную запись соотношений (1.5), введя линейную комбинацию точек

где обозначено α₁ = λ, α₂ = 1 - λ, причем α₁ ≥ 0, α₂ ≥ 0 и α₁ + α₂ = 1. Мы видим, что координаты любой точки отрезка АВ выражаются посредством линейной комбинации координат концов этого отрезка. В этом случае говорят, что координаты любой точки выпуклого множества АВ являются выпуклой линейной комбинацией соответствующих координат крайних точек. Можно обобщить это утверждение на случай произвольной комбинации точек с помощью следующего определения. Выпуклой линейной комбинацией точек X₁, X₂, ..., X_n называется любая точка X, если

где все α_i ≥ 0, α₁ + α₂ + ... + α_n = 1.

Иначе говоря, множество точек называется выпуклым, если вместе с любыми своими двумя точками оно содержит и произвольную выпуклую линейную комбинацию этих точек.

Выпуклый многоугольник обладает тем свойством, что он весь расположен по одну сторону от каждой из своих сторон (см. рис. 1.2). Всякая точка многоугольника, лежащая внутри него или на одной из сторон, за исключением вершин, может быть представлена в виде линейной выпуклой комбинации других точек этого многоугольника. Всегда можно сделать так, чтобы эта точка оказалась внутри некоторого отрезка, целиком принадлежащего выпуклому многоугольнику. Только вершины многоугольника не обладают этим свойством. Их иногда называют крайними или экстремальными точками (причина такого названия станет ясна в дальнейшем).

В пространстве трех и более измерений аналогами выпуклых многоугольников являются выпуклые многогранники. В пространстве трех измерений выпуклый многогранник представляет собой тело, гранями которого являются плоские выпуклые многоугольники (см. рис. 1.3). Вершины многогранника называются экстремальными точками.

Нетрудно убедиться, что уравнение a₁₁x₁ + a₁₂x₂ = b₁ (b₁>0) является уравнением прямой, которая в общем случае делит плоскость на две области: содержащую точку О и не содержащую этой точки.

Линейное уравнение с тремя переменными a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁ определяет в трехмерном пространстве некоторую плоскость, которая делит все пространство на два полупространства.

Аналогично каждое уравнение a_i1x₁ + a_i2x₂ + ... + a_inx_n = b_i системы (1.1) является уравнением некоторой гиперплоскости в n-мерном пространстве, которая рассекает все пространство на два полупространства. Для того чтобы определить одно из этих полупространств, следует использовать неравенство a_i1x₁ + a_i2x₂ + ... + a_inx_n ≤ b_i.

Система неравенств (1.3), будучи совместной, определяет общую часть всех этих полупространств, являющуюся выпуклым многогранником, поскольку этот многогранник оказывается весь расположен по одну сторону от любой из гиперплоскостей его образующих. Система уравнений (1.1) определяет грани и вершины этого выпуклого многогранника.

3. Значение линейной функции на выпуклом множестве. Выпуклые многоугольники и многогранники являются частными случаями выпуклых множеств, а именно являются ограниченными выпуклыми множествами. Задачи линейного программирования в основном сводятся к нахождению значений некоторой линейной функции на выпуклых много-угольниках или многогранниках, называемых многоугольниками или многогранниками решений. Следует, однако, заметить, что в общем случае система линейных неравенств может определять неограниченное выпуклое множество решений.

Пусть известно выпуклое множество, образующее совокупность решений системы уравнений (1.1). Линейная функция (1.2) в каждой точке этого выпуклого множества, т. е. для каждого решения системы (1.1), имеет вполне определенное значение. Нас будет интересовать вопрос о том, в каких точках выпуклого множества линейная функция (1.2) достигает максимального или минимального значения.

Всякое решение X (x₁, ..., x_n), компоненты которого x₁, x₂, ..., x_n неотрицательны и удовлетворяют системе (1.1), является допустимым решением или планом задачи линейного программирования. Планы, которые даются решениями, определяющими вершины многогранника решений, называются опорными планами.

Оптимальным решением задачи линейного программирования, как уже отмечалось, является оптимальный опорный план, который максимизирует (минимизирует) линейную функцию (1.2). Множество всех планов задачи линейного программирования выпукло, поскольку вместе с любыми двумя планами из этого множества оно содержит любую их линейную комбинацию.

Можно показать (см. [2,18]), что в тех случаях, когда множество планов задачи линейного программирования образует выпуклый многогранник, линейная функция (1.2) достигает своего оптимального значения в какой-либо из экстремальных точек (вершин выпуклого многогранника).

В частном случае, если функция достигает оптимального значения в двух или более соседних вершинах выпуклого многогранника, то она достигает оптимума также сразу в бесконечном числе точек, образующих ребро или грань, которым принадлежат эти вершины.

Таким образом, совокупность всех допустимых решений системы (1.1) представляет в общем случае выпуклое множество. Если же множество ограничено, то оно является многогранником в n-мерном пространстве. Функция цели (1.2) достигает своего максимального (минимального) значения в одной из экстремальных точек (вершин) этого многогранника.