
§ 5. Метод последовательного улучшения плана (симплексный метод)
Метод последовательного улучшения плана (далее для краткости мы будем называть этот метод общепринятым названием симплексный метод) позволяет найти решение любой задачи линейного программирования, проделав ограниченное число шагов, каждый из которых является алгебраическим преобразованием, производимым и установленным правилам.
1. Основная идея симплексного метода. Прежде всего для начала вычислений требуется, чтобы система уравнений (1.1) была приведена к такому виду, в котором какие-либо m неизвестных выражены через остальные n-m. Будем считать, что ранг матрицы А равен m (n>m). Предположим также, что свободные члены bi неотрицательны. В противном случае можно умножить правую и левую части уравнения, у которого свободный член отрицателен, на -1. Далее допустим, что неизвестные, которые выражены через остальные, есть x1, ..., xm. Таким образом, система (1.1) может быть записана в виде
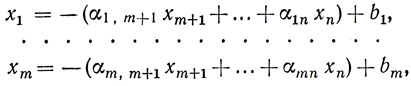
(1.7)
где b1≥0, ..., bm≥0 и коэффициенты α1,m+1, ..., αmn выражаются через a11, ..., amn. Неизвестные x1, ..., xm, которые находятся в левой части системы (1.7), образуют некоторый базис, поэтому эти неизвестные называются базисными. Остальные неизвестные являются небазисными (или свободными).
Будем считать для определенности, что требуется найти такое решение системы (1.1), которое обращает целевую функцию f = c1x1 + ... + cnxn в минимум.
Подставляя в функцию f вместо базисных неизвестных их выражения через небазисные, записанные в виде (1.7), представим функцию f с помощью свободных неизвестных xm+1, ..., xn в виде
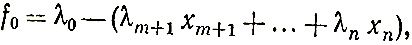
(1.8)
где все λ - постоянные коэффициенты.
Поскольку неизвестные xm+1, ..., xn свободные, то их можно положить равными 0. Тогда из системы (1.7) находим значения базисных неизвестных:
x1 = b1, ..., xm = bm.
Решение системы (1.7) (b1, ..., bm, 0, ..., 0) будет являться базисным решением, для которого значение функции f0 = λ0. Очевидно, здесь возможны два случая:
- Все числа λm+1, ..., λn неположительны, Тогда минимум функции f достигается при xm+1 = ... = xn = 0, т. е. полученное базисное решение является оптимальным, и задача решена.
- Среди чисел λm+1, ..., λn имеются положительные, например, λj>0, (m+1<j<n). В этом случае можно попробовать, не изменяя нулевых значений всех небазисных неизвестных, кроме xj, уменьшить функцию f за счет увеличения xj. При этом необходимо следить, чтобы ни одно из значений базисных переменных x1, ..., xm не было отрицательным.
Полагая в (1.7) и (1.8) все свободные переменные, кроме xj, равными 0, получаем
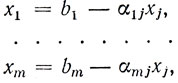
f1 = λ0 - λjxj, (λj>0).
Если все числа α1j, ..., αmj неположительные, то очевидно, что при всех xj≥0, x1, ..., xm также положительные числа и при xj→∞, f→-∞, т. е. минимум функции f не достигается.
Если среди чисел α1j, ..., αmj есть положительные, то xj нельзя увеличивать беспредельно. Пусть αkj = 0, где k = 1, 2, ..., m. Очевидно, что число xk = bk - αkjxj станет отрицательным, когда будет дано значение xj>bk/αkj. Поскольку xj входит во все числа x1,..., xm, среди этих чисел найдется по крайней мере одно xi, которое при увеличении xj станет отрицательным ранее других. Для того чтобы определить xi, найдем среди всех отношений bk/αkj наименьшее, которое обозначим bi/αij (αij>0).
Таким образом, bi/αij = min bk/αkj, где берутся все k, для которых akj>0. Обозначим это минимальное значение через δ. Очевидно, что δ>0. Если минимум достигается сразу при нескольких k, то за i можно брать любое из этих значений k.
Теперь xj можно увеличивать до величины δ, не опасаясь, что какое-нибудь xi станет отрицательным.
Положим
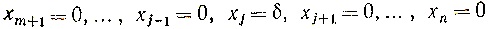
(1.9)
и найдем значения остальных неизвестных
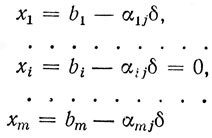
(1.10)
и целевой функции
f1 = λ0 - λjδ<f0, (λj>0).(1.11)
Итак, в результате проведенных преобразований получен новый базис x1, ..., xi-1xj, xi+1, ..., xn, в котором неизвестное xi заменено на xj (xj = δ), и при этом функция f уменьшилась, т. е. мы приблизились к искомому минимуму целевой функции.
Чтобы завершить первый шаг преобразований, остается только записать систему (1.7) и функцию (1.8) через новый базис. Для этого из уравнения для xi (старого базисного неизвестного) в системе (1.7) находим xj (новое базисное неизвестное):
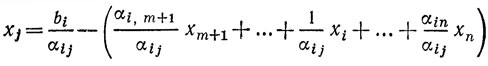
и подставляем это выражение вместо xj в остальные уравнения. В результате система оказывается разрешенной относительно нового базиса:
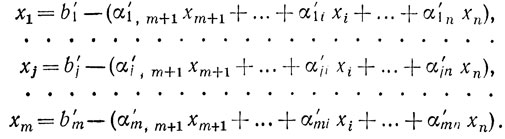
(1.12)
Правила для определения коэффициентов α'kl системы (1.12) через коэффициенты системы (1.7) будут даны позднее. Здесь выпишем только выражения для свободных членов системы (1.12):
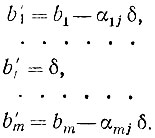
Все b'1, ..., b'm - числа неотрицательные, что следует из определения величины δ.
Целевую функцию также выразим через новые базисные переменные:
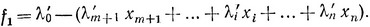
(1.13)
На этом заканчивается процесс вычислений первого шага.
Если искомое оптимальное решение не найдено, т. е. если среди коэффициентов λ'm+1, ..., λ'n имеются положительные, то процесс вычислений необходимо продолжить, производя аналогично вышеизложенному новую замену базиса. Второй шаг заканчивается новым выражением для функции f, из которого становится ясно, получено ли решение задачи или следует переходить к третьему шагу.
Приведенное выше описание основной идеи симплексного метода было дано конкретно для случая нахождения минимума целевой функции f. Небольшое изменение характера действий позволяет обобщить это описание также на случай отыскания максимума f. Для этого необходимо попытаться увеличить f0, если среди чисел λm+1, ..., λn есть неположительные. Определяя δ точно так же, как для случая минимизации f, из выражения (1.11) получим величину f1 = λ0 - λjδ>f0 (так как λj<0). Далее приходим к системе (1.12) и выражению (1.13), на которых заканчиваются вычисления первого шага.
Поясним все сказанное выше на простейшем примере. Пусть задана система ограничений
x1 + x2 = 1,
x2 - x3 = 2
и целевая функция
f = x1 + 2x2 + 3x3.
Требуется найти такое решение системы, которое обращает в максимум функцию f.
Запишем эту систему и функцию f в виде
x1 = 1 - x3,
x2 = 2 + x3,
f = 5 + 4x3.
Здесь неизвестные x1 и x2 образуют базис. Соответствующее базисное решение есть (1, 2, 0). Для этого решения значение функции f = 5. Поскольку x3 входит в f с положительным коэффициентом, можно попытаться увеличить f, увеличивая x3.
Из первого уравнения системы следует, что максимальное значение x3 = 1 (при x3>1 становится отрицательным x1).
Переходим к новому базису (x2, x3):
x2 = 3 - x1,
x3 = 1 - x1,
f = 9 - 4x1.
Увеличить f больше нельзя, так как x1 входит в f с отрицательным коэффициентом. Решение x1 = 0, x2 = 3, x3 = 1 является оптимальным базисным решением. Функция цели достигает максимума: f = 9.
Ввиду простоты задачи можно убедиться в этом непосредственными вычислениями.
Итак, мы описали основную идею симплексного метода. Однако проведение преобразований в общем случае все же требует выполнения довольно громоздких вычислений. Ниже будут даны общие правила и методы, позволяющие до некоторой степени упростить и формализовать расчеты, а также будут указаны возможные затруднения, которые могут при этом встретиться.
2. Выделение первого базиса. Предыдущий раздел начинался с предположения о том, что система уравнений (1.1) приведена к виду (1.7), в котором какие-либо m неизвестных (например, 1, 2, ..., m неизвестные) выражены через остальные (n - m) неизвестных. При этом предполагалось, что все свободные члены bi неотрицательны.
Предположение о возможности приведения системы (1.1) к системе (1.7) равносильно предположению о том, что из системы (1.1) можно непосредственно выделить базисное решение. В некоторых случаях это действительно легко сделать. Например, очень просто выделяется первый базис в том случае, если в каждое из m линейно-независимых уравнений одно из неизвестных x1, x2, ..., xn входит с коэффициентом +1, причем в остальных (m-1) уравнениях оно не встречается (как это имело место в примере, приведенном в предыдущем разделе). В том случае, если коэффициенты при этих неизвестных отличны от +1, очевидно, можно всегда сделать их равными +1, разделив левую и правую части уравнений на эти коэффициенты.
Первое базисное решение легко также получить для тех задач, в которых ограничения заданы в виде системы линейных неравенств вида
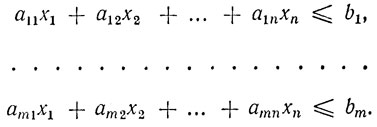
Для этого нужно превратить эту систему неравенств в систему уравнений таким образом, как было описано в § 1 этой главы. Добавив к левой части этих неравенств неотрицательные переменные xn+1, xn+2, ..., xn+m, мы получаем возможность сразу выделить базис.
Итак, в некоторых частных случаях процедура выделения первого базиса, т. е. возможность проведения преобразования системы (1.1) к системе (1.7), представляется весьма простой. Однако в большинстве случаев не всегда удается сразу найти путь для такого преобразования. Рассмотрим один из методов выделения первого базиса, называемый обычно "методом искусственного базиса".
Пусть система ограничений задана в виде (1.1), где все bi>0. Введем вспомогательные или так называемые искусственные неизвестные y1, y2, ..., ym, связанные с x1, x2, ..., xn уравнениями
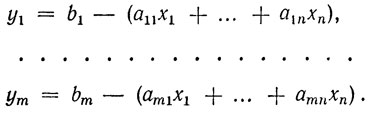
(1.14)
Очевидно, система (1.14) имеет то же самое решение, что и система (1.1), при условии y1 = 0, y2 = 0, ..., ym = 0. В системе (1.14) искусственные переменные y1, ..., ym образуют базис. Используя этот базис, можно перейти к другому базису, не содержащему ни одной искусственной неизвестной, например к x1, ..., xm.
Допустим, что после некоторых преобразований система (1.14) приведена к виду

(1.15)
где β1≥0, ..., βm≥0. В системе (1.15) мы имеем право положить y1 = 0, ..., ym = 0; тогда эта система становится эквивалентной системе (1.7). В системе (1.15) неизвестные x1, ..., xm образуют базис, т. е. тем самым задача выделения первого базиса решена.
Оказывается, что для перехода от системы (1.14) к системе (1.15) можно применить симплексный метод. Действительно, будем при помощи этого метода решать задачу о минимизации функции
F = y1 + y2 + ... + ym
при ограничениях, заданных системой (1.14) и при условиях
x1≥0, ..., xn≥0, y1≥0, ..., ym≥0.
Система (1.14) записана в таком виде (выделен базис y1, ..., ym), что к ней может быть непосредственно применен симплексный метод. После некоторого числа шагов искомый минимум, очевидно, будет получен, причем так как F≥0, то и min F≥0.
Однако, если min F≥0, система (1.15) не может иметь неотрицательных решений, для которых все y1 = 0, ..., ym = 0. Следовательно, и исходная система (1.14) также не может иметь неотрицательных решений, т. е. эта система не удовлетворяет условиям, которым должна удовлетворять система ограничений задачи линейного программирования, и эта задача в данном случае не имеет решения (система (1.14) несовместна).
Если min F = 0, то вследствие неотрицательности y1, y2, ..., ym должны быть равны 0 все искусственные неизвестные y1, ..., ym, входящие в базисное решение x1, ..., xm, y1, ..., ym, которое минимизирует функцию F. Это означает, что в случае min F = 0 данная система ограничений (1.14) совместна. Далее необходимо убедиться, что искусственные неизвестные не входят в базис. В противном случае следует проделать дальнейшие преобразования (описанные в предыдущем разделе), чтобы вывести их из базиса.
Таким образом, мы показали, как выделить первый базис для любой совместной системы ограничений, используемых в задачах линейного программирования. Укажем теперь некоторые формальные правила, облегчающие вычисления по алгоритму симплексного метода.
3. Алгоритм симплексного метода и симплексные таблицы. В настоящем разделе достаточно подробно излагается общий алгоритм симплексного метода, т. е. указывается совокупность математических операций, которые, будучи выполнены в определенной последовательности, обеспечивают получение решения задач данного класса.
Поскольку процесс решения задач линейного программирования симплексным методом является шаговым, оказывается удобным записывать результаты каждого шага решения в виде так называемых симплексных таблиц, заполняемых по определенным правилам. Каждое тождественное преобразование системы уравнений сводится к переходу от одной таблицы к другой.
Для простоты предположим, что нам известно первое базисное решение, т. е. систему уравнений задачи можно записать в виде
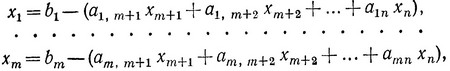
(1.7')
где все bi≥0.
Учитывая все сказанное в предыдущем разделе, можно считать, что это предположение нисколько не снижает общности изложения. Функцию цели будем пока записывать как в виде f1 = c1x1 + c2x2 + ... + cnxn, так и в виде
f1 = λ0 + (λm+1xm+1 + ... + λnxn),
где f1 - значение функции f, соответствующее первой симплексной таблице.
Составим первую симплексную таблицу.
В эту таблицу записываются в определенном порядке все величины, которые требуются в процессе решения задачи.
Метод составления таблиц представляется вполне очевидным, а ее форма является достаточно общепринятой. Последнюю строку этой таблицы принято называть "индексной" строкой.
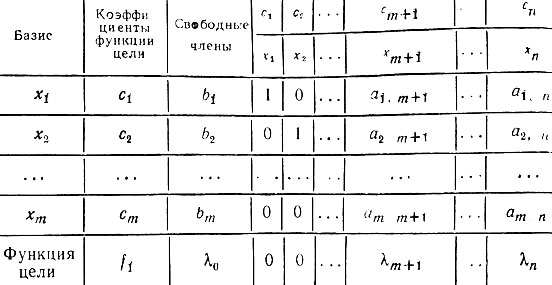
Таблица 1
В том случае, если все элементы индексной строки (кроме λ0) табл. 1 при решении задач на минимум отрицательны (или при решении задач на максимум - положительны), то полученное решение является оптимальным. Этим решением будет x1 = b1, x2 = b2, ..., xm = bm, xm+1 = 0, ..., xn = 0. Значение функции цели при этом, очевидно, равно f1 = c1b1 + c2b2 + ... + cmbm.
Если же среди элементов индексной строки есть положительные при решении задачи на минимум (отрицательные при решении задачи на максимум), то полученное решение не является оптимальным. В этом случае выбираем соответствующий наибольший по абсолютной величине элемент индексной строки. Выбранный элемент определяет ведущий столбец таблицы (например, столбец с номером s).
Далее составляем отношения свободных членов (третий столбец) к положительным элементам s-го столбца и выбираем из них наименьшее, как это было описано выше. Пусть этим наименьшим отношением будет br/ars, т. е. br/ars = min (bk/aks) (все aks>0). Тогда r-я строка называется ведущей строкой. На пересечении r-й строки и s-го столбца находится элемент ars, который называется разрешающим элементом.
Следующим этапом является переход к новому базису, в котором неизвестное xr из базисных переводится в небазисные, а неизвестное xs делается базисным. Этот переход означает переход ко второй симплексной таблице. Получим формулы, с помощью которых следует вычислять элементы новой таблицы.
Переход к новой таблице эквивалентен переходу от системы (1.7) к системе (1.12), который осуществляется с помощью следующих тождественных преобразований, а именно r-е уравнение системы (1.7) следует разрешить относительно переменной xs:
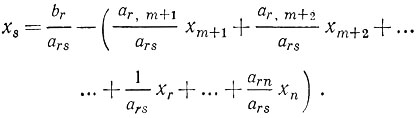
Это выражение для xs подставляем во все остальные уравнения и функцию f. Например, подстановка значения xs в k-е уравнение (k≠s) системы (1.7') приводит к уравнению
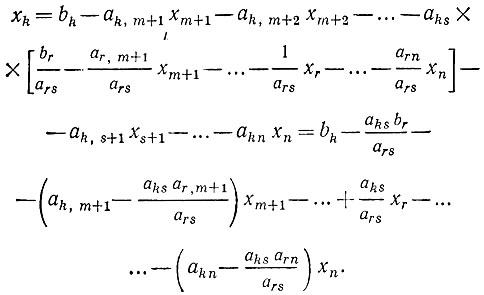
аналогично подстановка значения xs в функцию цели f приводит к выражению
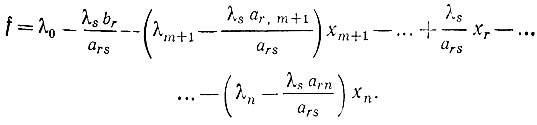
Таким образом, из выражения для ха следует, что элементы r-й строки новой таблицы равны соответствующим элементам старой таблицы, разделенным на разрешающий элемент
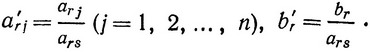
Элементы s-uj столбца новой таблицы все равны 0, за исключением a'rs = 1, так как xs стало базисным переменным и больше не входит в правую часть системы уравнений.
Чтобы получить любой другой элемент новой симплексной таблицы, нужно от соответствующего элемента прежней таблицы отнять произведение элемента ведущей строки на элемент ведущего столбца, разделенное на разрешающий элемент, т. е.
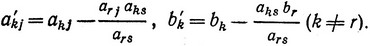
Как легко видеть, по этой формуле могут быть также вычислены коэффициенты функции f или все элементы индексной строки новой симплексной таблицы, т. е.
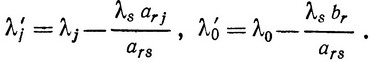
Вторая симплексная таблица (табл. 2) имеет такой же вид, как и симплексная табл. 1.
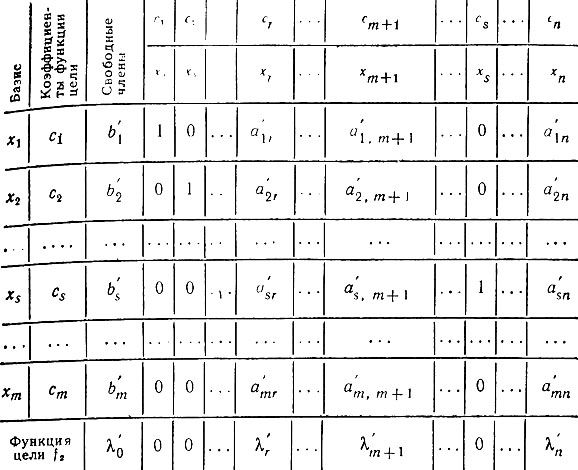
Таблица 2
Только теперь переменная xs стала базисной переменной и коэффициенты bi, aij, λj заменены на b'i, a'ij, λ'i.
Если сразу все эти элементы оказались отрицательными (при задаче на минимум) или положительными (при задаче на максимум), то оптимальное решение получено, и функция цели принимает значение
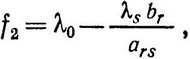
где f2 - значение функции цели, полученное из второй симплексной таблицы.
Соответственно, если эти условия не выполняются, необходимо переходить к следующей симплексной таблице, проводя тождественные преобразования по установленным выше правилам.
Укажем дополнительно еще одну возможность вычисления элементов индексной строки исходя из представления функции f в виде f = c1x1 + c2x2 + ... cnxn. Для этого преобразуем данное выражение следующим образом:
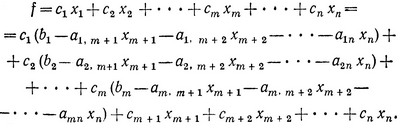
Объединив свободные члены и коэффициенты при xm+1, xm+2, ..., xn, получим
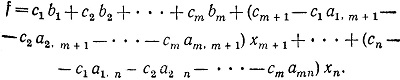
Таким образом, мы получили явное выражение для I коэффициентов функции цели через коэффициенты aij, bi и ci:
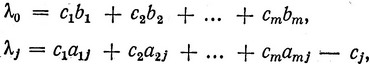
где f = m + 1, m + 2, ..., n.
Обозначим c1a1j + c2a2j + ... cmamj через γj. Тогда λj = γj - cj и элементы индексной строки могут вычисляться по этой формуле после того, как получены все элементы aij (i = 1, 2, ..., m). При этих вычислениях используются элементы c1, c2, ..., cn, повторяющиеся в каждой симплексной таблице.
Итак, после конечного числа шагов будет либо получено оптимальное решение, или установлено, что задача не имеет решения. При этом, однако, иногда могут встретиться так называемые случаи вырождения и зацикливания.
Случай вырождения встретится, если свободный член уравнения, содержащего разрешающий элемент, равен нулю. В этом случае после очередного шага значение функции цели не увеличится (или не уменьшится). Поскольку значения базисных неизвестных решения равны свободным членам соответствующих уравнений (небазисные неизвестные мы полагаем равными нулю), то случай вырождения равносилен тому, что одна или несколько базисных неизвестных равны 0. В этом случае (l + 1)-е значение функции цели совпадает с l-й ее значением, т. е. fl+1 = fl. Ясно, что это произойдет в том случае, если в последовательности базисов некоторые из них будут повторяться. При этом может случиться, что на каждом из последующих шагов имеет место вырождение, т. е. fl = fl+1 = fl+2 = ... . В этом случае говорят, что в процессе решения задачи произошло зацикливание. Отметим, однако, что при решении конкретных экономических задач случаи зацикливания крайне редки, причем его всегда можно избежать, если изменить последовательность выбора базисов.
Указанная выше последовательность операций определяет алгоритм симплексного метода. Этот алгоритм позволяет решать задачи линейного программирования на ЭВМ.
Проиллюстрируем симплексный метод решения на примере задачи распределения ресурсов. Допустим, предприятие может выпускать два вида изделий, на изготовление которых идет три вида ресурсов, выделяемых этому предприятию в количествах, ограниченных величинами b1 = 100, b2 = 120 и b3 = 150 единиц. На изготовление тысячи штук изделий первого вида расходуется a11 = 10 единиц ресурсов b1, a21 = 20 единиц ресурсов b2 и a31 = 20 единиц ресурсов b3. Соответственно на изготовление тысячи изделий второго вида расходуется a12 = 20 единиц ресурсов b1, a22 = 10 единиц ресурсов b2 и a32 = 20 единиц ресурсов b3. Известно, что оптовые цены изделий первого вида P1 = 7 тыс. руб. и второго вида P2 = 13 тыс. руб. (за тысячу штук), а себестоимость тысячи этих изделий соответственно C1 = 5 тыс. и C2 = 10 тыс. руб. Требуется составить оптимальный план выпуска изделий этих двух видов, обеспечивающий получение максимальной прибыли предприятия. Предполагается, что эти виды изделий могут производиться в любых соотношениях (сбыт обеспечен). Математически эта задача формулируется следующим образом: найти
max f = (P1 - C1)x1 + (P2 - C2)x2
при ограничениях
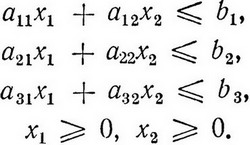
Подставляя в уравнение численные значения, получим следующую задачу: найти
max f = 2x1 + 3x2
при ограничениях
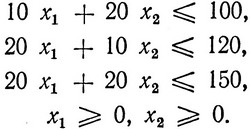
Введем искусственные переменные x3, x4, x5 и перепишем уравнения таким образом, чтобы выделить первое базисное решение и подойти к составлению первой симплексной таблицы:
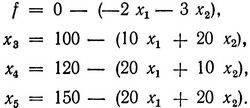
Составим первую симплексную таблицу (в несколько упрощенном виде).
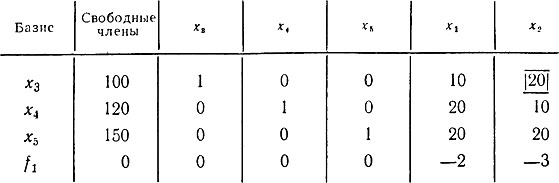
Таблица 1'
Выбираем столбец, отвечающий x2 как ведущий, и находим разрешающий элемент, сравнивая отношения 100/20 = 5, 120/10 = 12 и 150/20 = 7,5. Разрешающим элементом будет ars = a12 = 20. Далее по соответствующим формулам вычисляем коэффициенты a'ij, b'i и λ'j, которые записываем во вторую симплексную таблицу.

Таблица 2'
Так как в индексной строке остался отрицательный элемент, то оптимальное решение еще не получено. В столбце, соответствующем x1, разрешающим элементом является a'21 = 15. Затем вычисляем коэффициенты a"ij, b"i, λ"j переходим к следующей симплексной таблице.
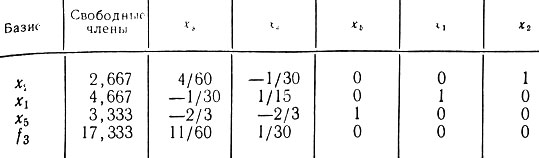
Таблица 3'
Теперь получено оптимальное решение: x1 = 4,667 и x2 = 2,667 тыс. шт. При этих значениях x1 и x2 функция цели достигает максимума f3 = fmax = 17,333 (тыс. руб.), в чем нетрудно убедиться непосредственно. При этом 3,333 единицы ресурсов b3 окажутся неизрасходованными, т. е. предприятие от них может отказаться. Отметим, однако, что третий знак после запятой не является точным, так как в нем накапливается ошибка округления, производимого во время расчетов.
|
ПОИСК:
|
© ECONOMICS-LIB.RU, 2001-2022
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'