
Глава I. Линейное программирование
§ 1. Основная задача линейного программирования
Цель, которая обычно ставится при составлении плана, заключается в максимизации или минимизации некоторого ограниченного количества средств (денег, промышленного сырья, машинного оборудования, продуктов питания и т. д.), что выражается математически в виде нахождения минимума или максимума функции некоторого числа переменных. В свою очередь эти переменные, каждая из которых выражает наличные ресурсы, подвержены ограничениям, задаваемым математически в виде системы неравенств или уравнений. В том случае, если эти ограничения и сама функция (называемая обычно целевой функцией или функцией цели), минимум (максимум) которой ищется, выражаются линейными функциями, говорят о том, что решается задача линейного программирования. Итак, линейное программирование-это математическая дисциплина, изучающая методы нахождения наименьшего или наибольшего значения линейной функции (линейной формы) нескольких переменных, удовлетворяющих конечному числу линейных уравнений или неравенств. Общая математическая формулировка основной задачи линейного программирования выглядит следующим образом.
Дана система m линейных уравнений, содержащая n переменных
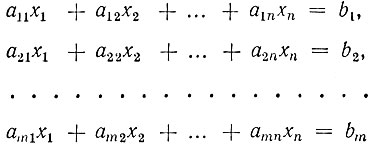
(1.1)
и линейная функция этих переменных
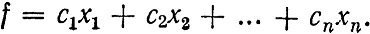
(1.2)
Требуется найти такое неотрицательное решение системы (1.1)
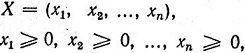
для которого линейная функция (1.2) принимает минимальное или максимальное значение. В сокращенном виде система уравнений (1.1) и функция (1.2) могут быть записаны следующим образом:
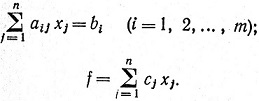
Уравнения системы (1.1) называются ограничениями данной задачи. Часто, однако, ограничения, которые наложены на переменные x1, x2, ..., xn, задаются не в виде системы уравнений, а в виде системы линейных неравенств вида
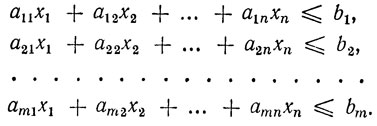
(1.3)
Всякую задачу с ограничениями (1.3) можно привести к основной задаче. Действительно, добавим в левую часть неравенств (1.3) некоторые неотрицательные переменные y1, y2, ..., yn, такие, чтобы система неравенств (1.3) превратилась в систему уравнений
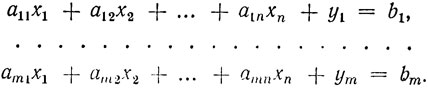
(1.3')
Покажем, что всякое решение1 системы (1.3) является также решением системы (1.3'). Пусть a1, a2, ..., an есть какое-нибудь решение системы (1.3). Это означает, что
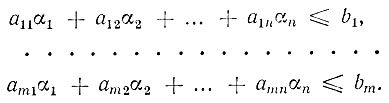
1 (В дальнейшем, если это специально не оговорено, мы будем иметь в виду только неотрицательные решения.)
Если в левую часть этих неравенств добавить числа β1, β2, ..., βm такие, чтобы неравенства превратились в равенства, то, очевидно, значения переменных x1 = α1, x2 = α2, ..., xn = αn, y1 = β1, y2 = β2, ..., ym = βm будут решением системы уравнений (1.3). Таким образом, решение системы (1.3), т. е. числа α1, α2, ..., αn, удовлетворяет также и системе (1.3').
Можно аналогичным образом доказать и обратное: если x1 = α1, ..., xn = αn, y1 = β1, ..., ym = βm есть какое-нибудь решение системы (1.3'), то x1 = α1, x2 = α2, ..., xn = αn является решением системы (1.3). Система уравнений (1.3) называется эквивалентной системе неравенств (1.3) и всякую систему линейных неравенств можно заменить эквивалентной ей системой линейных уравнений, т. е. любая задача линейного программирования, в которой ограничения заданы в виде системы (1.3), может быть приведена к основной задаче линейного программирования.
Аналогичное утверждение можно сделать в том случае, когда ограничения заданы системой неравенств вида

Для того чтобы от этой системы перейти к эквивалентной системе уравнений, нужно от левой части неравенств отнять соответствующие неотрицательные переменные.
Очевидно, что в наиболее общем случае ограничения могут быть заданы в виде смешанной системы, включающей равенства и неравенства (общая задача линейного программирования). В силу вышеизложенного такая смешанная система может быть сведена к системе уравнений вида (1.1). Всякое неотрицательное решение системы (1.1) называется допустимым решением или планом задачи. Допустимое решение, максимизирующее (минимизирующее) линейную функцию (1.2), называется оптимальным решением или оптимальным планом. Часто, однако, оптимальное решение S называют просто решением задачи.
Существует непосредственная связь между задачами максимизации и минимизации, так как каждую задачу о максимизации можно заменить эквивалентной задачей о минимизации, если, сохранив неизменными ограничения, изменить знак всех коэффициентов функции цели.
Система (1.1) называется совместной, если существует хотя бы одна совокупность значений переменных x1 = α1, x2 = α2, ..., xn = αn, тождественно удовлетворяющих всем уравнениям системы. Вопрос о существовании решения системы (1.1) решается в курсе высшей алгебры, где установлены условия, при которых система (1.1) имеет единственное решение, бесконечное множество решений или ни одного решения, когда говорят, что система несовместна. При этом среди чисел α1, ..., αn могут быть не только положительные или нулевые, но и отрицательные числа. Однако нас интересуют не любые решения системы (1.1), а только неотрицательные, т. е. нулевые или положительные, которые только и являются решениями задач линейного программирования.
|
ПОИСК:
|
© ECONOMICS-LIB.RU, 2001-2022
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'