1. Межотраслевой баланс

Нужды высокоразвитого хозяйства, являющегося типичным для XX в., и в особенности нужды планируемой, управляемой экономики, возникшей в результате социалистической революции, вызвали потребность в конкретных и развернутых экономических показателях и характеристиках. Одной из форм практической реализации этой потребности было создание схемы межотраслевого баланса. Впервые эта схема была разработана в 20-х годах советскими учеными, затем она получила развитие в работах американского экономиста В. Леонтьева, а с 50-х годов широко используется для совершенствования народнохозяйственного планирования в СССР (см. гл. VI, § 4).

Идея межотраслевого баланса чрезвычайно проста. Ее может легко усвоить любой человек. Ведь получив заработную плату, он должен распределить, куда уйдут его деньги. А это (хотя человек того и не подозревает) и есть составление балансовых отношений в их простейшей форме. На той же идее сопоставления затрат и результатов основан и межотраслевой баланс. Он называется так потому, что балансовые отношения, включенные в него, характеризуют взаимосвязи между различными отраслями народного хозяйства.

В табл. 26 схематически изображены балансовые соотношения отраслей. Как их следует понимать? Примем условно, что в народном хозяйстве имеются только четыре отрасли: 1 - производство электроэнергии, 2 - топливная промышленность, 3 - черная металлургия и 4 - легкая промышленность. В таблице величина x_ij выражает объем продукции i-й отрасли, затрачиваемой при функционировании j-й отрасли. В соответствии с принятыми условиями это означает, что продукция первой отрасли распределяется на следующие нужды: x₁₁ - количество электроэнергии, затрачиваемое при производстве электроэнергии; x₁₂ - количество электроэнергии, затрачиваемое в топливной промышленности. Электроэнергия расходуется и в черной металлургии, и в легкой промышленности, потребности которых определят соответственно величины x₁₃ и x₁₄.

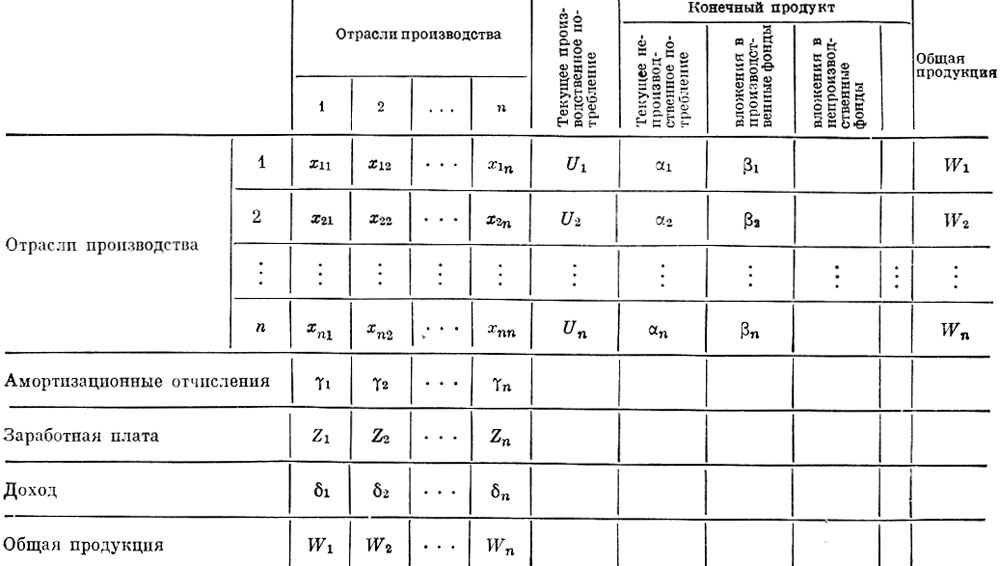
Таблица 26

Однако электроэнергию потребляют не только отрасли производства. Потребителями являются население, государственные и культурные учреждения. Обозначим объем конечного продукта i-й отрасли через V_i. Он складывается из непроизводственного потребления α_i (включая и вложения в непроизводственные фонды) и накопления - вложения в производственные фонды β_i. Через U_i обозначим объем продукции i-й отрасли, затрачиваемой при функционировании всех четырех отраслей. Через W_i обозначим общий объем производства i-й отрасли. Тогда приходим к следующим соотношениям:

(1)

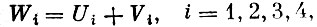
где

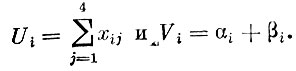
Эти уравнения получаются в результате суммирования по строкам табл. 26 и указывают, как используется и распределяется производственная продукция. Например, первые из них (i=1) означают, что вся произведенная электроэнергия (W₁) распределяется между четырьмя отраслями производства (U₁= x₁₁+x₁₂+x₁₃+x₁₄), непроизводственным потреблением и накоплением (V₁=α₁+β₁).

Однако отрасль можно анализировать не только с точки зрения распределения ее продукции, а и с точки зрения затрат на производство в данной отрасли. Так, для получения продукции черной металлургии требуются и электроэнергия, и топливо, и изделия легкой промышленности (спецодежда и т. п.). Помимо этого, в j-й отрасли имеются затраты на амортизационные отчисления (γ_j), на заработную плату (Z_j), а также доход (δ_j), возникающий при реализации продукта отрасли. Таким образом, для затрат на производство продукции j-й отрасли можно записать следующее равенство:

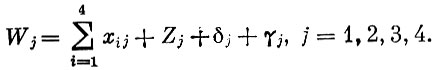
Последнее из этих уравнений (j=4) означает, согласно принятым выше условиям, что стоимость продукции легкой промышленности равна стоимости затраченных в ней продуктов всех четырех отраслей и амортизации плюс заработная плата работников легкой промышленности и доход, полученный от реализации продуктов легкой промышленности^*. Аналогичным образом, но, понятно, для своих отраслей трактуются и остальные уравнения.

^* (Матрица (таблица) межотраслевого баланса может строиться как в натуральных единицах измерения (тонны металла и т. п.), так и в стоимостной форме (в каких-то базовых неизменных ценах). Здесь имеется в виду именно последняя форма баланса.)

Рассмотренные балансовые соотношения очень важны, так как на их основе могут рассчитываться чрезвычайно существенные экономические характеристики - коэффициенты прямых и полных затрат. Коэффициент прямых затрат характеризует средний расход продукта i-й отрасли на выпуск единицы продукта j-й отрасли. Он обозначается a_ij и, например, в принятых выше символах коэффициент прямых затрат электроэнергии на продукцию металлургии имеет вид a₁₃=x₁₃/W₃.

Однако расход электроэнергии на выпуск металла не исчерпывается прямыми ее затратами. В производстве металла участвует топливо, на создание которого была использована электроэнергия, а также многие другие ингредиенты, производство которых тоже потребовало затрат электроэнергии. Все эти затраты должны быть учтены как связанные с выпуском металла. Добавив к прямым затратам электроэнергии в металлургии ее расход в смежных отраслях (в той части, в которой эти отрасли участвуют в производстве металла), после соответствующих пересчетов получаем коэффициент полных затрат электроэнергии на выпуск металла.

Коэффициент полных затрат, который обозначается через c_ij, характеризует, сколько всего нужно произвести продукции в i-й отрасли, чтобы обеспечить выпуск продукции в отрасли j. Математически полные затраты находятся с помощью специального приема - обращения матрицы. Используя этот прием, рассчитывают все коэффициенты полных затрат. Понятно, что полные затраты могут существенно отличаться от прямых затрат. Так, в межотраслевом балансе СССР за 1959 г., охватывавшем 83 отрасли, прямые затраты черного металла на производство электроэнергии составляли 14,4 руб. на тысячу рублей продукции, тогда как полные затраты были равны 45,4 руб.

Поясним, каким образом используется межотраслевой баланс в планировании производства. Уравнения (1) в случае любого числа отраслей имеют вид

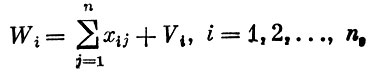
а так как a_ij= x_ij/W_j, то это соотношение можно преобразовать в

(2)

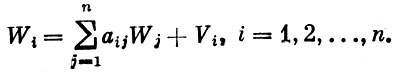
Получена система n уравнений с 2n неизвестными общими объемами производства всех отраслей и их же конечными продуктами. Поскольку неизвестных больше, чем уравнений, то эта система неопределенна. Для того чтобы сделать ее определенной, необходимо, исходя из каких-то соображений, указать n из этих величин. На практике обычно по некоторым отраслям задаются уровни конечного продукта (как правило, по тем, которые по преимуществу служат для удовлетворения общественных и личных потребностей), по другим же, играющим главную роль в материальном производстве, задаются общие объемы выпуска.

Покажем, каким образом осуществляется решение системы уравнений межотраслевого баланса. Систему (2) можно записать в матричной форме как

(2′)

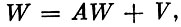
где W - вектор объемов производства; V - вектор уровней конечного продукта; А - матрица коэффициентов прямых затрат.

Рассмотрим случай, когда задано W, т. е. заданы объемы производства по всем отраслям. Тогда вектор V определяется формулой

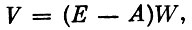
где Е - единичная матрица. Другой случай, когда заданным оказывается V, т. е. заданы уровни конечного продукта по всем отраслям. Вектор W определяется в этом случае формулой

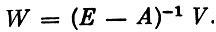
Если объемы производства заданы только по части отраслей, а по остальным известны уровни конечного продукта, то решение системы (2) незначительно усложняется. Если же пользоваться не коэффициентами прямых затрат (a_ij), а коэффициентами полных затрат (c_ij), то система (2) преобразуется и приводится к виду

(3)

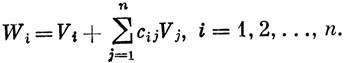
Система (3) может использоваться подобно системе (2), но с ее помощью легче находятся W_i по заданным V_i.

Необходимо сказать, что формулы (2) и (3) верны только в предположении, что коэффициенты прямых затрат a_ij остаются неизменными при возможных изменениях объемов выпуска продукции. Конечно, эта гипотеза не очень строго соблюдается в действительности. Поэтому указанными формулами можно пользоваться как весьма приближенными и то лишь при не очень больших отклонениях объемов выпуска от базисных данных.

Несмотря на простоту и удобство в использовании, схема межотраслевого баланса имеет и существенные недостатки. Например, немалые трудности при составлении балансовых соотношений возникают из-за того, что предприятия почти каждой отрасли производят не только продукцию, относящуюся непосредственно к своей отрасли, но и другие виды продукции. Скажем, шарикоподшипниковый завод выпускает и мясорубки, и фигурные коньки, и другие предметы широкого потребления. Кроме того, нормы затрат для одного вида продукции, производимого на разных предприятиях, как правило, не одинаковы даже для предприятий одной и той же отрасли. Именно поэтому при изменении объема производства трудно ожидать, что он будет реализован с теми же (средними) затратами.

Но даже если и преодолеть эти трудности, не удается избавиться от главного недостатка схемы межотраслевого баланса. Эта схема представляет собой по сути как бы моментальную фотографию сложившегося состояния экономики: в ней никак не учитывается развитие народного хозяйства. Получаемые средние уровни затрат не отражают многообразия возможных технологий, реализации достижений технического прогресса. Естественно поэтому, что на основе межотраслевого баланса нельзя решать задачи экономической динамики - определять оптимальные темпы и пропорции развития различных отраслей народного хозяйства. На частичное устранение этих недостатков направлены некоторые народнохозяйственные динамические модели, построенные на базе межотраслевого баланса.

В качестве примера приведем динамическую модель межотраслевого баланса, позволяющую учитывать капиталовложения в различные отрасли, а также связь между общими объемами производства в различные периоды. В ней через ΔK_ij обозначено количество продукции i-й отрасли, затрачиваемое в данный период на капитале вложения в j-ю отрасль, а номер периода указывается индексом t. С такими обозначениями основная система уравнений межотраслевого баланса преобразуется в

(4)

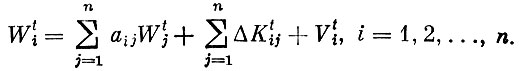
Если предположить, как это обычно делается, что необходимые для отрасли капиталовложения пропорциональны приросту продукции отрасли, т. е.

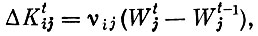
то уравнения (4) приводятся к виду

(4′)

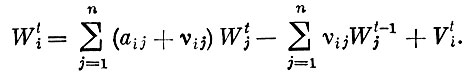
Величины v_ij носят название коэффициентов вложений. Эти коэффициенты позволяют выявить необходимую связь, существующую между периодами. Из системы (4′), зная общие объемы производства по всем отраслям в период t - 1 и зная объемы потребления, можно найти объемы производства в период t.

Такого рода модели учитывают динамику развития экономической системы. И если, как отмечалось, статический межотраслевой баланс - это моментальная фотография, то динамические модели межотраслевого баланса можно считать чем-то вроде документального кинофильма. Но ни те, ни другие модели не могут полностью решить главной задачи экономической динамики - рассчитать оптимальные темпы и пропорции развития отраслей народного хозяйства. Прогресс в решении этой задачи будет, вероятно, достигнут на других путях. Мы имеем в виду, прежде всего, интенсивно разрабатываемую сейчас теорию динамических моделей оптимального планирования.