
3. Игровые модели экономики
До сих пор изложение теории игр было у нас довольно далеким от экономики, если, конечно, не считать, что "выигрыш" и "проигрыш", когда они выражают некие денежные суммы, могут рассматриваться как экономические термины. Но настала пора покинуть мир абстрактных математических моделей и ступить на конкретную почву хозяйственных связей и отношений.
Пусть экономическая система состоит из n предприятий и каждое из них выступает и в роли поставщика, и в роли потребителя. Например, предприятие k характеризуется множеством производственных возможностей Qk. Элементы этого множества - векторы xk - определяют количества затрачиваемых и выпускаемых ингредиентов (отрицательные компоненты определяют затраты а положительные - выпуск). Таким образом, хозяйственная самостоятельность предприятия моделируется возможностью выбора векторов xk из множества Qk.
Однако такое описание недостаточно. Ведь предприятие к, так же как и все остальные предприятия, не независимо. Между предприятиями существуют определенные связи, а также имеются общие ограничения, характеризующие систему в целом. Такие ограничения можно представить как
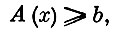
где x=(x1, ..., xn), A(x) - известная вектор-функция, а b - s-мерный заданный вектор. За соблюдение общих ограничений отвечает (n+1)-й участник экономической системы - некий планирующий орган (назовем его ПО).
Каждый участник экономической системы имеет свою цель. ПО стремится обеспечить максимально возможную прибыль в масштабах всей системы φ(x)=φ(x1, ..., xn). Предприятия же хотят максимизировать свои прибыли, исчисленные по существующим ценам. Налицо конфликтная ситуация - каждое предприятие заинтересовано в повышении цен на свою продукцию и в снижении цен на потребляемые ингредиенты. Какую же стратегию следует выбирать каждому предприятию, т. е. какие векторы затрат и выпуска выбирать и как назначать цены на продукцию?
Если сделать ряд сугубо математических предположений относительно вида различных множеств и функций, упомянутых в описании экономической ситуации, то можно доказать следующий интересный факт. В данной модели существуют равновесные стратегии для каждого предприятия (отклонение от которых не выгодно никому), а также соответствующие им цены (которые устанавливаются ПО) на все ингредиенты, производимые и потребляемые в системе.
Отыскание равновесных стратегий может быть организовано в виде следующего многошагового процесса. На каждом шаге ПО назначает цены на все ингредиенты, имеющиеся в системе, и предлагает предприятиям выбирать такие производственные программы, которые при этих ценах максимизируют их прибыль. Предприятия решают свои локальные задачи максимизации и сообщают оптимальные решения в ПО. На основании полученной информации ПО уточняет локальные ограничения и определяет лучший план и новые цены. Далее процесс повторяется. Если на двух последующих шагах планы предприятий не изменятся, значит найдено оптимальное решение. В противном случае каждый следующий шаг ведет к увеличению глобальной прибыли системы.
Рассмотренная ситуация довольно условна. Чтобы сделать ее немного реалистичнее, нужно привлечь более сложный и более тонкий аппарат теории игр.
Пусть имеется n предприятий, производящих n различных продуктов. Предприятие j выбирает свой производственный план yj из множества возможных планов Yj. Наряду с предприятиями имеются и потребители, которые покупают продукты по ценам p1, p2, ..., ps. Множества xi(i = 1, 2, ..., m) - наборы различных продуктов, доступные i-му потребителю. Предполагается, что предпочтение, которое i-й потребитель оказывает различным наборам продуктов, устанавливается функцией предпочтения Ui(x), где x - выбранный набор. Будем считать, что вся прибыль предприятий выплачивается потребителям таким образом, что i-й потребитель получает долю αij прибыли j-го предприятия. Понятно, что
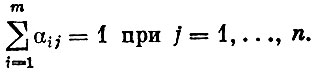
Налицо конфликтная ситуация. С одной стороны - предприятия, стремящиеся максимизировать свою прибыль, заинтересованы в повышении цен. С другой стороны - потребители, стремящиеся максимизировать полезность приобретенных продуктов в условиях ограниченности средств, заинтересованы в снижении цен. Какой стратегии должна следовать каждая из сторон?
Делая ряд предположений относительно множеств Yj, Xi и функции предпочтения U(x), возможно доказать следующий факт - для описываемой модели существует конкурентное равновесие. Это означает, что можно найти такие величины  1,
1,  8,
8, 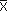 1, ...,
1, ..., 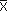 m,
m, 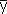 1, ...,
1, ..., 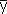 n, которые удовлетворяют следующим условиям:
n, которые удовлетворяют следующим условиям:
(1)
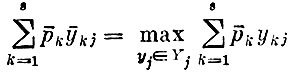
(здесь ykj - количество k-го продукта, выпускаемое в j-м производственном плане. Равенство утверждает, что прибыли предприятий максимальны, когда в качестве цен назначены равновесные цены).
Набор 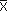 i при всех i максимизирует Ui(x) на множестве
i при всех i максимизирует Ui(x) на множестве
(2)
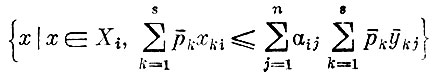
(здесь xki - количество k-го продукта в наборе потребления x i-ro потребителя. Это условие означает, что i-й потребитель максимизирует пользу от приобретаемых им продуктов по таким наборам этих продуктов, которые, во-первых, принадлежат множеству доступных для него наборов, а, во-вторых, приобретение их укладывается в имеющиеся у него финансовые ресурсы).
(3)
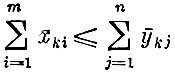
при всех k. Кроме того,
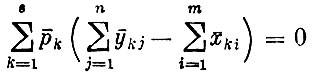
(спрос должен быть удовлетворен. Если же какого-нибудь продукта производится больше, чем требуется, то цена его равна нулю).
Итак, состояние равновесия в экономике - это такое положение, когда ни одно предприятие не может добиться большей прибыли при сложившихся ценах и ни один потребитель не может приобрести больше без дополнительных затрат. "Игрокам" не выгодно отклоняться от своих оптимальных смешанных стратегий.
Описанная модель принадлежит известным американским математикам-экономистам Эрроу и Дебре. Ситуация, которая формулируется ею, несколько более реалистична, чем та, что рассматривалась в начале параграфа. Однако и эта ситуация достаточно условна. Вообще игровые модели экономики имеют пока не столько практическое, сколько методологическое значение. Они, пожалуй, только еще прокладывают пути, которые в будущем найдут широкое использование в управлении процессом общественного производства.
|
ПОИСК:
|
© ECONOMICS-LIB.RU, 2001-2022
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'