2. Поиск оптимальных стратегий

После того как выяснено, что оптимальные стратегии существуют, естественно, возникает другая проблема - как найти эти стратегии. Существует ряд методов, предназначенных специально для такой цели. Здесь мы обсудим два из них.

Эквивалентность матричной игры и задачи линейного программирования. Чрезвычайно важным и исключительно полезным оказался тот факт, что всякая игра двух лиц с нулевой суммой эквивалентна некоторой задаче линейного программирования. Это означает, что по заданной платежной матрице игры можно построить такую пару задач линейного программирования, решения которых определяют оптимальные стратегии обоих игроков. И, наоборот, всякой задаче линейного программирования можно сопоставить игру так, что оптимальные стратегии игроков дадут решения исходной задачи и двойственной к ней. Мы не будем приводить здесь полного доказательства эквивалентности, а ограничимся тем, что покажем, как от игры перейти к задаче линейного программирования.

Задана платежная матрица

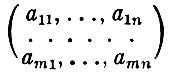
Пусть игрок А будет выбирать свои стратегии с вероятностями, равными соответственно 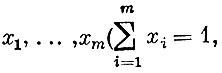x_i≥0). Если игрок В выбирает свою первую стратегию, то ожидаемый выигрыш игрока А составит

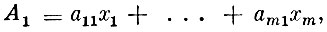
если В выбирает вторую стратегию, то выигрыш составляет

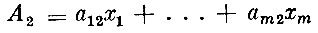
и т. д. вплоть до n-й стратегии, которой соответствует выигрыш игрока А, равный

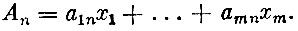
Понятно, что наименьший выигрыш, который может получить А, равен 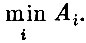Обозначим эту величину через x_m+1 т. е. 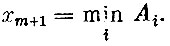Так как игрок А хочет добиться максимально возможного наименьшего выигрыша, то, выбирая свою стратегию, он должен решить следующую задачу.

Найти

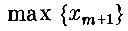
при ограничениях

(1)

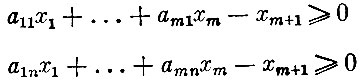
(величина x_m+1 не превосходит ожидаемого выигрыша игрока А ни при одной из стратегий игрока В)

(2)

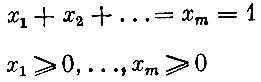
(условия, которым должна удовлетворять всякая смешанная стратегия).

Легко заметить, что целевая функция и ограничения, полученные нами, выражают задачу линейного программирования. Совершенно аналогичные рассуждения показывают, что игрок В, отыскивая оптимальную стратегию, должен также решать задачу линейного программирования, только не на максимум, а на минимум. Тем самым доказана возможность сведения игры к решению двух задач линейного программирования. Так как аппарат линейного программирования очень хорошо разработан, возможности отыскания оптимальных стратегий в матричных играх существенно расширяются.

Итеративный метод решения игр (метод Брауна). В 1951 г. американский математик Браун предложил метод отыскания оптимальных стратегий в матричных играх, опирающийся на известное правило - принимать то или иное решение на основании изучения предыстории, накопленного опыта. Суть метода состоит в том, что игроки, прежде чем сделать ход, разыгрывают как бы "в уме" целый ряд фиктивных партий, учитывая стратегии друг друга и всякий раз выбирая оптимальную чистую стратегию против смешанной стратегии по всем прошлым партиям противника.

Только что прочитанная фраза трудна для понимания. Поясним ее примером. Пусть платежная матрица имеет вид

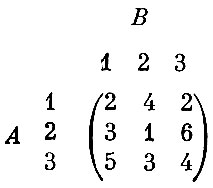
Последовательность фиктивных партий опишем в виде этапов (итераций), на каждом из которых тот или иной игрок выбирает свою стратегию.

Первая партия

I этап. Игрок А выбирает любую из своих стратегий, например стратегию 3, и результат выбора сообщает игроку В.

II этап. Игрок В выбирает лучший ответ на этот ход - свою стратегию 2.

Вторая партия

III этап. Игрок А, зная, что В выбирал стратегию 2, отвечает на нее лучшим образом - своей стратегией 1.

IV этап. Игрок В знает, что А один раз применял стратегию 3 и один раз - стратегию 1. Он ищет поэтому наилучший ответ против смешанной стратегии (1/2, 0, 1/2), т. е. стратегии 1 и 3 равновероятны, стратегия 2 не используется. Таким ответом служит стратегия 3, так как ей соответствует наименьший ожидаемый проигрыш в 3 единицы.

Третья партия

V этап. Игрок А знает, что В один раз применял стратегию 2 и один раз - стратегию 3, т. е. ему нужно отвечать на смешанную стратегию (0, 1/2, 1/2). Лучший ответ - стратегия 2 или стратегия 3, так как они дают одинаковый ожидаемый выигрыш в 8/3 единицы.

В результате разыгрывания трех фиктивных партий получены такие приближенные смешанные стратегии: для игрока А - (0, 1/2, 1/2); для игрока В - (1/3, 1/3, 1/3). Процесс улучшения этих стратегий путем "обучения на опыте" может быть продолжен сколь угодно долго.

На каждом этапе каждый игрок старается максимизировать свой средний выигрыш, считая, что противник будет использовать свои стратегии с теми же частотами, что и до этого этапа. Доказано, что если каждый из игроков имеет единственную оптимальную смешанную стратегию, то при неограниченном увеличении числа партий находимые описанным выше путем приближенные смешанные стратегии стремятся к оптимальным стратегиям обоих игроков. Правда, для достижения оптимума требуется очень много времени, что резко снижает практическую ценность итеративного метода.