1. Игра двух лиц с нулевой суммой и ее обобщения

Здесь и в дальнейшем игрой будет называться совокупность правил, определяющих возможные действия участников игры - игроков. Ранее мы уже упоминали термин "стратегия", понимая под ним синоним к словам "план", "поведение", "управление". В теории игр стратегия - это система поведения, в простейшем случае выбор одной из имеющихся у игрока альтернатив. Игра заканчивается платежом проигравшего игрока выигравшему. Следовательно, должна быть задана функция выигрыша - правило, сопоставляющее величину выигрыша избранной паре стратегий.

В случае игры двух лиц естественно считать их интересы прямо противоположными - игра антагонистическая. Таким образом, выигрыш одного игрока равен проигрышу другого (сумма выигрышей обоих игроков равна нулю, отсюда и название - игра с нулевой суммой). Будем рассматривать игры, в которых у каждого игрока имеется конечное число альтернатив. Функция выигрыша для такой игры двух лиц с нулевой суммой может быть задана в матричной форме (в виде платежной матрицы).

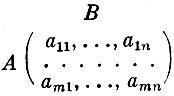
Отсюда название подобных игр - матричные игры. Поясним, как происходит одноходовая игра. Игрок А выбирает одну из m строк (i-ю) платежной матрицы. Не зная результата его выбора, игрок В выбирает один из n столбцов (j-й) той же матрицы. Элемент a_ij определяет сумму выигрыша одного игрока и проигрыша (-a_ij) другого игрока.

Основной вопрос, который возникает здесь, состоит в следующем: существуют ли наилучшие, оптимальные способы ведения игры для каждого из игроков, т. е. имеются ли у них оптимальные стратегии? Поясним, в каком смысле следует понимать оптимальность стратегий. Каждый игрок считает своего противника "разумным", т. е. старающимся выиграть у него как можно больше. При таком предположении естественно считать стратегии игроков оптимальными, если один из них, например первый, не уменьшит своего выигрыша при любом изменении стратегии второго игрока. Соответственно второй игрок не увеличит своего проигрыша при любом изменении стратегии первого игрока. Прежде чем дать ответ на поставленный вопрос, рассмотрим несколько примеров.

Пусть задана такая платежная матрица

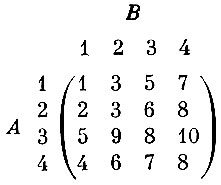
Легко заметить, что для игрока А третья стратегия лучше всех остальных (говорят, что она доминирует над остальными стратегиями). Элементы третьей строки матрицы больше соответствующих элементов всех остальных строк. Следовательно, используя эту стратегию, игрок А сможет получить больший выигрыш, чем если бы он избрал любую другую стратегию (каково бы при этом ни было действие В). Совершенно аналогично, игроку В выгоднее всего применять первую стратегию, так как элементы первого столбца меньше соответствующих элементов всех остальных столбцов. (Напомним, что элементы платежной матрицы выражают проигрыш игрока В.) Применяя эту стратегию, игрок В потеряет меньше всего. В результате элемент матрицы a_3,1 определяет выигрыш А и проигрыш В, равный 5.

Итак, вывод. Если каждый игрок имеет стратегию, доминирующую над остальными, то эта доминирующая стратегия и является оптимальной.

Теперь более сложный пример. Платежная матрица имеет вид

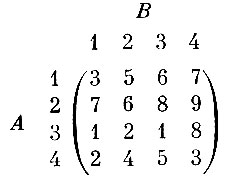
Как быть в этом случае? Если А выберет первую стратегию, то он может выиграть 7 (В выбирает четвертую стратегию). Так как каждый игрок считает своего противника разумным, то самое лучшее для А выбрать вторую стратегию - выигрыш во всяком случае окажется не менее 6 единиц. Точно так же игроку В выгодно выбрать вторую стратегию, ведь при этом больше 6 единиц уж он не проиграет. (При любом другом выборе не исключена возможность проигрыша больше, чем 6 единиц.) Вывод - для каждого игрока выгоднее всего выбирать свою вторую стратегию.

Обратимся к рассмотрению общего случая. Имеется платежная матрица

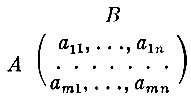
Если игрок А выбирает i-ю строку, то он выигрывает по меньшей мере 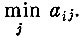Так как i он может выбрать любым, то для него естественно постараться сделать 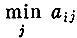возможно большим, т. е. выбирать его так, что-бы получить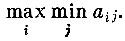

Игрок В, рассуждая таким же образом, может наверняка обеспечить себе выигрыш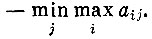

Итак, игрок А уверен, что он получит не меньше, чем 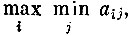а игрок В может помешать ему получить больше, чем 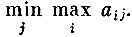Можно показать, что для этих величин всегда справедливо неравенство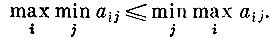

Если же вдруг окажется, что (*)^*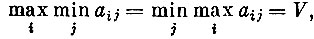

^* (Если бы равенство (*) выполнялось для всякой матрицы, то вопрос о существовании оптимальных стратегий был бы тем самым решен. К сожалению, однако, такое равенство выполняется далеко не всегда. Например, для матрицы )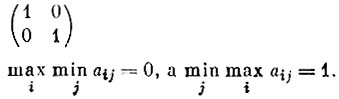

то понятно, что те значения i и о, при которых это равенство достигается, представляют собой оптимальные стратегии игроков. Величина V носит название цены игры.

Так как равенство (*) обеспечивает существование оптимальных стратегий обоих игроков, то важную роль играют необходимые и достаточные условия его выполнения. К их установлению мы сейчас и перейдем. Прежде всего введем одно необходимое для дальнейшего определение: точка (i₀, j₀) называется седловой точкой матрицы, если выполняются условия

(1)

(2)

(элемент a_i0j0 наименьший в строке и наибольший в столбце)^*.

^* (Это определение седловой точки рекомендуем сравнить с другим ее определением, данным в га. III, § 2.)

Пользуясь таким определением, можно сформулировать необходимые и достаточные условия выполнения равенства (*). Они содержатся в следующей теореме (которую мы приведем без доказательства): для того чтобы выполнялось условие

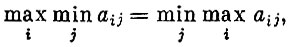
необходимо и достаточно, чтобы матрица имела седловую точку. Кроме того, если (i₀, j₀) есть седловая точка матрицы, то

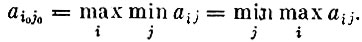
Понятно, как найти оптимальные стратегии игроков, когда платежная матрица имеет седловую точку. Но к сожалению, многие матрицы не имеют седловых точек. Как же быть с такими матрицами? Обсудим идею, которая позволила преодолеть эту трудность.

Стратегию, состоящую в выборе той или иной строки платежной матрицы, будем называть чистой стратегией. Понятно, что если матрица имеет седловую точку, то соответствующие оптимальные чистые стратегии взаимно уравновешены - ни одному из игроков не выгодно отклоняться от своей оптимальной чистой стратегии. Если же он отклонится, то гарантированный выигрыш его уменьшится (или проигрыш увеличится). В том случае, когда матрица не имеет седловой точки, такой уравновешенности среди чистых стратегий уже нет. Естественно поэтому попытаться расширить множество стратегий так, чтобы в новом, более богатом множестве стратегий уже нашлись и взаимно уравновешенные пары стратегий. Для этой цели, наряду с чистыми стратегиями будем рассматривать их "вероятностные смеси", т. е. создадим ситуацию, при которой игрок не знает заранее, выбор какой альтернативы им будет сделан.

Снова рассмотрим игру с такой платежной матрицей 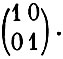Пусть игрок А решает выбрать свою первую или вторую стратегии в зависимости от исхода бросания монеты - если выпадает орел, то первая стратегия, если - решка, то вторая. Вероятности, с которыми выбираются стратегии, 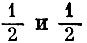- определяют смешанную стратегию игрока А. (Конечно, она не единственна. Могли быть и другие вероятности, но осуществляемые иным механизмом.) Легко подсчитать математическое ожидание выигрыша игрока А. В нашем случае оно не зависит от того, выберет ли игрок В свою первую или вторую стратегии, и составляет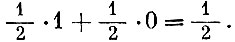

Перейдем теперь к общему определению смешанной стратегии. Допустим, что игрок А для определения своей стратегии применяет метод случайного выбора, причем такой, что вероятность выбора первой строки - x₁ второй - x₂ и т. д. вплоть до x_m. Будем называть смешанной стратегией игрока А такой упорядоченный набор m чисел x₁, x₂, ..., x_m, который удовлетворяет двум условиям:

(1)

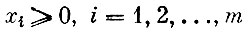
(вероятности выбора каждой строки неотрицательны);

(2)

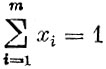
(не может быть, чтобы ни одна из m строк не была выбрана). Совершенно аналогично упорядоченный набор n чисел y₁, ..., y_n, который удовлетворяет условиям

(1)

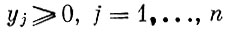
(2)

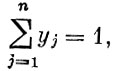
называется смешанной стратегией игрока В.

По сути дела образование смешанных стратегий игроков равносильно расширению исходной матрицы путем добавления к ней бесчисленного множества строк и столбцов. Понятно, что всякая чистая стратегия является частным случаем смешанной стратегии - достаточно все величины x_i (или y_j), за исключением одной, положить равными нулю, а оставшийся x (или y) положить равным единице. Обратное неверно. Значит, действительно, вновь построенное множество смешанных стратегий шире множества чистых стратегий.

Поясним теперь, в каком смысле следует говорить об оптимальности смешанных стратегий. Рассмотрим простенькую задачу об А и В, которые играют в теннис. Игрок В хочет с помощью математических методов исследовать, целесообразно ли ему в игре с А выходить к сетке, или более правильно играть у задней линии. Из опытных данных предполагается известной матрица, характеризующая частоты выигрышей игрока В в зависимости от возможного расположения игроков на поле:

Матрица показывает, что если, например, игрок В у сетки, а игрок А у задней линии, то в 80 случаях из 100 выигрывает игрок В. Столь же ясный смысл имеют и другие элементы матрицы. Эта матрица не имеет седловой точки и, значит, у игроков не существуют оптимальные чистые стратегии и они должны использовать смешанные стратегии. Пусть игрок А выбирает свою первую стратегию (игру у сетки) с вероятностью x, а вторую (игру у задней линии) - с вероятностью 1 - x. Аналогично игрок В выбирает первую стратегию с вероятностью y, а вторую - с вероятностью 1 - y. Вопрос состоит в том, чтобы наилучшим образом выбрать величины x и y.

Понятно, что частота выигрышей игрока В зависит от выбора величин x и y. Подсчитаем математическое ожидание этой частоты. Оно равно

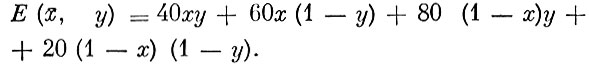
После элементарных преобразований получаем

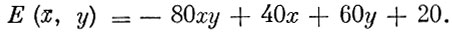
Значения x и y естественно выбирать из условий экстремальности E(x, y), т. е. следует взять частные производные от E(x, y) по x и по y, приравнять их нулю и из этих условий найти x и y. Выполнив все эти действия, окончательно получим седловую точку

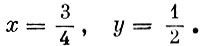
Полученный результат можно истолковать так. Ни один из игроков не имеет оптимальной чистой стратегии. Но если они будут выбирать стратегии, пользуясь подходящим случайным механизмом (таким, который для игрока В с одинаковой вероятностью выбирает каждую из двух его стратегий, а для игрока А первую стратегию выбирает с вероятностью 3/4, вторую же соответственно с вероятностью 1/4), то это лучшее, что они могут сделать. Ни одному игроку не выгодно отклоняться от указанных вероятностей, так как при этом он может только уменьшить частоту своих выигрышей. (Так как платежные матрицы различны для различных игроков, мы не рекомендуем читателям-теннисистам формально использовать полученные результаты.)

Факт существования оптимальных смешанных стратегий не является случайным, присущим именно рассмотренной игре. В основной теореме теории игр утверждается" для всякой матричной игры двух игроков с нулевой суммой существуют оптимальные смешанные стратегии у каждого из игроков. Таким образом, важное свойство уравновешенности стратегий - невыгодность для каждого из игроков отклониться от своей оптимальной стратегии - сохраняется и в смешанных стратегиях.

Отметим теперь некоторые наиболее важные обобщения теории игр двух лиц с нулевой суммой, пригодные для анализа более сложных ситуаций. Прежде всего естественно рассмотреть тот случай, когда выигрыш одного игрока не равен проигрышу второго, т. е. игру с ненулевой суммой. Может представиться несколько вариантов подобной игры - кооперативная игра, в которой игроки имеют неограниченную свободу сообщений до игры, и некооперативная, где никакие сообщения между игроками не разрешаются.

Обратимся к кооперативной игре двух лиц с ненулевой суммой. Элементами платежной матрицы служат в ней не числа, а пары чисел. И матрица может, например, иметь вид

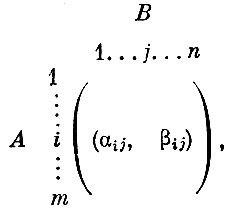
что означает: если игрок A выбирает стратегию i, а игрок В стратегию j, то выигрыш А равен α_ij, а В - β_ij.

Оказывается, что для подобных игр нарушаются все основные свойства антагонистических игр - они не всегда обладают уравновешенными стратегиями, а если есть несколько уравновешенных стратегий, то они не обязательно обеспечивают одинаковый выигрыш и могут не быть взаимозаменяемы. Читатель может убедиться в этом сам, построив подходящим образом матрицу такой игры

Иначе решается вопрос в некооперативной игре. В 1951 г. американский математик Нэш доказал, что всякая некооперативная игра с конечным множеством чистых стратегий имеет по меньшей мере одну уравновешенную пару смешанных стратегий. Если такая пара единственна, то она и обеспечивает решение игры. Если их несколько, но все они взаимозаменяемы, то говорят, что игра разрешима в смысле Нэша. При отсутствии же такой взаимозаменимости решение игры вообще не определено. (Пусть читателя не удивляют столь неполные результаты. Сложнее стал объект исследования - беднее заключения.)

Рассмотрим теперь, как изменится картина, если допускаются сообщения между игроками до игры, т. е. неантагонистическая игра двух лиц является кооперативной. Будем предполагать, что все соглашения, которые заключают игроки, обязательно должны ими выполняться. Кроме того, в результате переговоров не меняются оценки исходов игры, т. е. сохраняется исходная платежная матрица. Естественный вопрос - как найти, да и как определить, что считать решением игры в этом случае? Ради простоты дальнейшие пояснения будут носить чисто геометрический характер.

Пару чисел, выражающих выигрыши игроков А и В, будем изображать на плоскости точкой, у которой абсцисса - выигрыш игрока A, а ордината - выигрыш игрока В. Множество выигрышей, соответствующих всем возможным смешанным стратегиям обоих игроков, представляет собой некоторое выпуклое множество Q (см. рис. 18).

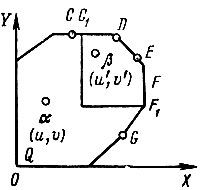
Рис. 18

Понятно, что если множеству Q принадлежат две точки α и β таких, что u′>u и v′>v, то ни один из игроков никогда не будет выбирать стратегию, которой соответствуют платежи, изображенные точкой а - это им невыгодно. Стало быть, решение игры следует искать среди тех стратегий, которым соответствуют точки Q, расположенные на рисунке справа и вверху, т. е. точки ломаной CDEFG. Точки этой ломаной носят название оптимального множества Парето. Если вне этого множества сотрудничество игроков имеет смысл, то в самом оптимальном множестве Парето ни о каком сотрудничестве уже речи нет - игрок А хочет получить платеж, которому соответствует точка G, а игрок В - точка С. Так как каждый игрок при переговорах согласится получить не меньше, чем гарантированный уровень выигрыша без всяких переговоров, то из множества Парето можно выделить подмножество C₁DEFF₁, носящее название переговорного множества игры. В таком множестве должна быть выбрана единственная точка, которая и будет решением игры. Выбор этой точки дело не очень легкое, он во многом зависит от "разумности" критериев, лежащих в основе игровой ситуации.

Еще сложнее проблемы, возникающие при игре n лиц. Дело в том, что при n>2 возможно создание коалиций, более могущественных, чем любой из игроков в отдельности. Для этих игр естественным образом обобщается понятие точки равновесия. Доказано, что всякая конечная игра n лиц имеет по меньшей мере одну точку равновесия в смешанных стратегиях. К сожалению, в этих играх нет ни взаимозаменяемости, ни эквивалентности уравновешенных стратегий, и, кроме того, оптимальное множество Парето и переговорное множество определяются гораздо более сложным образом.

Игры, которые были рассмотрены до сих пор, имели конечное множество чистых стратегий. На практике нередко оказывается необходимым изучать и такие игры, в которых игроки производят выборы из бесконечных множеств стратегий. Опишем модель подобной игры. Игрок А выбирает элемент x из множества R₁, игрок В выбирает элемент y из множества R₂ (обычно в качестве множеств R₁ и R₂ рассматривают замкнутые интервалы [0, 1]). Задана функция двух переменных Ф (x, y), характеризующая выигрыш первого игрока при таких выборах. Каким образом следует производить выбор каждому игроку? Игры описанного типа носят название непрерывных игр. Доказано, что если функция Ф(x, y) непрерывна, всегда существуют оптимальные смешанные стратегии для обоих игроков. Только понятие смешанной стратегии теперь вводится несколько иначе, с использованием более тонкого математического аппарата.