4. Стохастическое программирование

В практике планирования нередко встречаются задачи оптимизации, учитывающие случайный характер некоторых параметров. Такого рода задачи решаются методами стохастического программирования. В этих задачах случайными могут быть элементы технологической матрицы, размеры потребности (т. е. правые части ограничений), цены и другие факторы. Их случайный характер связан с тем, что невозможно, особенно при планировании на длительный период, указать значения всех коэффициентов и нормативов с полной определенностью. Они всегда могут измениться, либо по причине каких-нибудь непредвиденных событий, либо просто под влиянием времени и притом на неизвестную величину.

Вот, например, экономическая проблема, для решения которой нужны методы стохастического программирования. На предприятие по ремонту автомобилей в течение года поступают заказы на выполнение тех или иных работ. Заранее неизвестно, когда, какие и в каком количестве заказы поступят. Здравый смысл подсказывает, что если набор станков на этом предприятии мал, то оно сможет выполнять только ограниченный круг работ и будет производить их медленно. В результате заказчики предпочтут обратиться к услугам других, более совершенных предприятий (если, конечно, такие предприятия существуют), а эта авторемонтная организация будет терпеть убытки, которые естественно измерять величиной прибыли, не полученной из-за слабости материальной базы. В то же время ясно, что если набор станков очень разнообразен и число их велико, то в течение длительного срока многие станки будут бездействовать, и, следовательно, затраты на их приобретение окупятся очень не скоро.

Надо думать, что существует промежуточное оптимальное решение этой проблемы. Оно, правда, не может быть представлено как требование достичь максимума прибыли, поскольку сумма прибылей за год является случайной величиной. В подобных случаях в качестве целевой функции обычно выбирается либо математическое ожидание прибыли^*, вычисляемое на основе известных вероятностей поступления заказов, либо вероятность того, что размер прибыли окажется не меньше заданного. Доказано, что решение вопроса в первом случае при условии линейности ограничений сводится к обычной задаче линейного программирования, второй же требует для своего исследования специальных методов.

^* (Математическим ожиданием или средним значением случайной величины x, принимающей значения x₁, x₂, .., x_n с вероятностями, равными, соответственно p₁, p₂, ..., p_n, называется величина 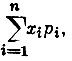, обозначающаяся обычно .)

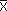Укажем еще две задачи, в которых естественно учитывать случайные факторы. При планировании сельскохозяйственного производства урожайности культур на различных участках, строго говоря, следует считать случайными, так как они зависят от погодных и других условий, предсказать которые точно невозможно. Точно так же невозможно предсказать число пассажиров, которые окажутся на той или иной авиалинии, но тем не менее необходимо определить количество самолетов, обслуживающих каждую линию. По-видимому, читатель без труда сможет пополнить список таких задач.

В чем же состоят основные трудности при решении задач стохастического программирования? Их несколько. Прежде всего далеко не всегда легко даже правильно поставить задачу, т. е. добиться того, чтобы вероятностная модель хорошо описывала изучаемый процесс. А когда такая модель построена, требуется еще создать методы для ее исследования. Все это привело к тому, что, несмотря на многочисленную литературу, этот раздел математического программирования является наименее разработанным. В основном изучаются лишь отдельные частные постановки задач и методы их решения.

Приведем две возможные постановки задачи стохастического программирования и обсудим подходы к их решению.

Рассмотрим первую постановку. В некоторых ситуациях представляется неприемлемым, чтобы при каких бы то ни было случайных воздействиях, могущих иметь место, нарушались бы предписанные ограничения. Подобная ситуация описывается, например, следующей моделью.

Найти вектор x (детерминированный!), доставляющий максимум математическому ожиданию линейной целевой функции

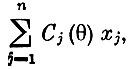
при условиях

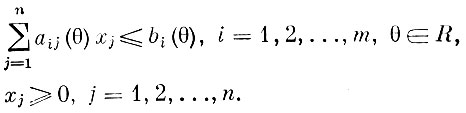
Здесь величины a_ij(θ), b_i(θ) и C_j(θ) принимают случайные значения в зависимости от значения, принимаемого случайным параметром θ. Каждая реализация θ определяет многогранник допустимых планов соответствующей задачи линейного программирования (реализация параметра θ носит название состояния природы или элементарного события, а множество возможных значений этого параметра R называется множеством возможных состояний природы или пространством элементарных событий). При любом состоянии природы должны удовлетворяться все поставленные ограничения, поэтому допустимым, естественно, считать план, который принадлежит всем возможным многогранникам допустимых планов. Если пересечение этих многогранников пусто, то допустимого плана задачи не существует.

Изложенная постановка носит название жесткой или одноэтапной задачи стохастического программирования. Выбор плана в ней должен производиться заранее, с расчетом на все возможные состояния природы, в один этап. Последующих корректировок не предполагается.

Несколько слов о методах решения. Если множество состояний природы конечно, то, очевидно, стохастическая задача может быть сведена к такой детерминированной задаче.

Найти

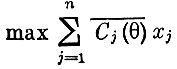
при условиях

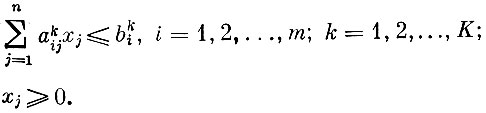
Здесь через C_j‾(θ) обозначено среднее значение случайной величины C_j(θ), взятое относительно всех возможных состояний природы, K - число возможных состояний природы, а a^k_ij и b^k_i - коэффициенты, соответствующие реализации k-го состояния природы. Если число K велико, то трудность определяется большой размерностью задачи. В случае бесконечного числа состояний природы приходится устраивать подходящую конечномерную аппроксимацию.

Перейдем теперь к рассмотрению второй возможной постановки задачи стохастического программирования. Одноэтапная задача не всегда адекватно описывает реальную ситуацию. Очень часто представляется желательным и возможным корректировать план, после того как становится известным состояние природы. Постановка задачи, в которой предусмотрена такая возможность, носит название нежесткой или двухэтапной задачи стохастического программирования. Рассмотрим эту постановку на примере конкретной задачи планирования сельскохозяйственного производства в условиях неопределенности.

Пусть имеется поле площадью S гектаров, которое предполагается засеять двумя культурами с урожайностями, равными соответственно a₁ ц/га и a₂ ц/га. Известны цены на эти культуры - C₁ руб./ц и C₂ руб./ц. Предусмотрена и возможность орошения поля, причем цена воды составляет α руб./м³. Первая культура для нормального созревания обязательно должна получать b₁ м³/га воды, а вторая - b₂ м³/га. Эта вода попадает в почву частично в результате дождей, частично благодаря системе орошения. Для простоты предположим, что возможен один из двух исходов: либо лето влажное, когда выпадает d₁ м³/га воды, либо лето сухое - d₂ м³/га воды, причем вероятность влажного лета р, а сухого - 1-р. При таких условиях требуется составить план посева (определить площади под каждую культуру) и орошения, который обеспечивает максимум суммарного среднего дохода (математического ожидания дохода).

Введем ряд обозначений. Если x - площадь, которая отводится под первую культуру, то под вторую культуру остается площадь S - x. Стратегия орошения - количество кубометров воды, требующееся дополнительно на гектар поля, определяется величинами:

В результате решения должны быть найдены величины x, y¹₁, y¹_2, y²₁ и y²₂. Приступим к построению модели. Так как мы предположили, что потребности каждой культуры в воде обязательно должны удовлетворяться, то должны выполняться такие равенства:

(1)

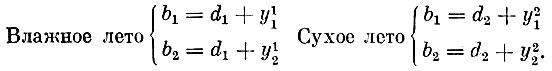
Величина x должна удовлетворять разумному физическому ограничению

(2)

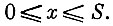
Целевая функция, математическое ожидание чистого дохода, складывается из дохода от реализации обеих культур по известным ценам минус средние затраты на орошение, исчисленные в предположении, что влажное лето случается с вероятностью p, а сухое - с вероятностью 1-p, т. е. она может быть записана так:

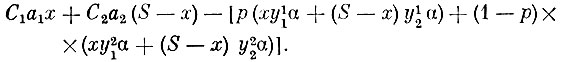
Оптимизационная задача состоит в том, чтобы найти максимум целевой функции при условиях (1) и (2). Нетрудно показать, что если из условий (1) определить величины y¹₁, y¹₂, y²₁, y²₂ и подставить их в целевую функцию, то в данном случае получится обычная задача на максимум линейной функции от x.

Итак, рассмотрены две возможные постановки задачи стохастического программирования. Надо сказать, что имеется и общая постановка такой задачи, но здесь не стоит ее излагать, поскольку это достаточно сложный и специальный вопрос. С помощью постановки подобных задач можно решать проблемы управления запасами при неполной информации о спросе, выбрать наилучший план внесения удобрений в почву и составить оптимальные планы осуществления многих других экономических мероприятий.

Отметим только, что в общем случае двухэтапная задача может быть сведена к задаче выпуклого программирования и поэтому для ее решения пригодны методы решения таких задач. Если же двухэтапная задача имеет линейную структуру, то она сводится к блочной задаче линейного программирования и может быть решена с помощью соответствующих специальных методов.