3. Целочисленное программирование

Задача о размещении производства уже не один раз использовалась в этой книге для разъяснения методов математического программирования. Поэксплуатируем ее еще раз. Рассмотрим небольшую, но весьма существенную модификацию этой задачи.

Пусть имеется n пунктов A₁, A₂, ..., A_n, в которых могут быть размещены предприятия, выпускающие определенный продукт. Производственные мощности этих предприятий x_i могут принимать лишь конечное множество значений, например 1, 2, 3 конвейерные линии, 5, 7, 8 однотипных агрегатов (печей, котлов) и т. п. Собственно, число этих мощностей не только конечно, но оно не может быть дробным. Иначе говоря, производственные мощности принимают определенные целочисленные значения (точнее, кратные некоторой единице). Для каждого пункта известна зависимость производственных затрат от выпуска, т. е. функция f_i(x_i). В целях упрощения будем считать ее линейной, т. е. f_i(x_i)=C_ix_i. Кроме того, заданы m пунктов потребления этого продукта с объемами потребления, равными соответственно B₁, B₂, ..., B_m, а также матрица транспортных затрат с элементами C_ij. Задача, как и раньше, состоит в размещении предприятий, определении их производственных мощностей и организации перевозок таким образом, чтобы суммарные затраты по производству и транспортировке были минимальными.

Обозначая через x_i объем "продукта, производимого в i-м пункте, а x_ij - количество продукта, перевозимое из A_i в B_j, приходим к следующей задаче.

Найти 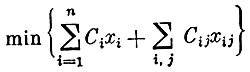(суммарные затраты по производству и транспортировке)

при условиях

(1) 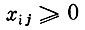(перевозятся неотрицательные количества продукта);

(2) 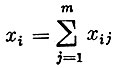(произведенное количество продукта полностью доставляется потребителям);

(3) 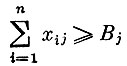(каждый пункт потребления получает продукт в объеме, не меньшем заданного);

(4) x_i - принимает заданные целочисленные значения^*.

^* (При решении практических вопросов особенно часто возникают такие задачи целочисленного программирования, в которых переменные принимают лишь два значения: нуль и единица. Экономически это означает, что то или иное возможное решение принимается или отвергается. Например, строить или не строить домну, приобретать или не приобретать машину и т. п.)

Задачи, в которых имеются ограничения типа (4) или сводящиеся к ним, получили название задач целочисленного программирования. Их отличает от линейно-программных моделей, казалось бы, сущий пустяк - добавление условия (4). Но из-за такого "пустяка" при решении подобных задач возникают большие трудности. Дело в том, что оптимальное решение в этом случае не обязательно находится в одной из вершин многогранника, задаваемого условиями (1)-(3), и обычные методы линейного программирования, использующие это обстоятельство, оказываются бессильными при решении задач целочисленного программирования.

Разработан, однако, ряд специальных методов, пригодных именно для такого класса задач. Простейший и наименее точный из них состоит в решении линейной задали с ограничениями (1)-(3) и последующим округлением результатов так, чтобы они удовлетворяли и условию (4). Точный метод, дающий оптимальное решение целочисленной задачи, впервые был предложен американским математиком Р. Гомори.

Мы ограничимся здесь подробным изложением идеи метода Гомори, не останавливаясь на формальном описании алгорифмов.

Так как задача целочисленного программирования отличается от обычной задачи линейного программирования только условием (4), то естественно попытаться хоть как-нибудь использовать для ее решения хорошо разработанный аппарат линейного программирования. Так и поступим. Решим задачу линейного программирования без условия (4). Если окажется, что в оптимальном плане величины x_i принимают целочисленные значения, то исходная задача решена - условие (4) выполнилось автоматически.

Однако столь приятное событие происходит крайне редко - обычно величины x_i не принимают целочисленных значений. Чтобы лучше понять суть дела, обратимся к наглядной иллюстрации. Для простоты будем говорить о плоском случае (две переменных), хотя все рассуждения сохраняют силу и для любого числа переменных. Ограничения (1)-(3) определяют на плоскости некоторый многоугольник Q, в вершине P которого, если нет условия (4), достигается минимум целевой функции. Внутри этого многоугольника и на его границе имеется конечное множество точек R (на рис. 15 они обозначены кружочками), которым соответствуют планы с целочисленными значениями переменных.

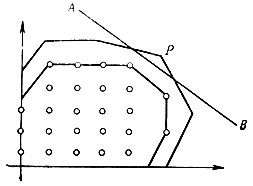
Рис. 15

Для дальнейшего нам потребуется ввести несколько определений. Множество R′ является выпуклой оболочкой множества R, если оно состоит из всевозможных выпуклых линейных комбинаций точек множества R. Опорным планом задачи линейного программирования называется такой план, который геометрически изображается крайней точкой многогранника допустимых планов. Те способы, которые используются в опорном плане с ненулевой интенсивностью, образуют базис опорного плана, а соответствующие переменные (координаты плана) называются базисными переменными. Естественно, остальные переменные называются небазисными.

Сравнительно легко показать, что всякий оптимальный опорный план задачи линейного программирования, рассматриваемой на множестве R′, является также оптимальным опорным планом той же задачи, но рассматриваемой на дискретном множестве R. Исходя из этого утверждения вроде бы можно предложить такой способ решения задачи целочисленного программирования: а) определить множество R целых точек многоугольника ограничений Q; б) образовать его линейную выпуклую оболочку R′; в) на множестве R′ решить задачу линейного программирования без условия целочисленности. Полученное решение и будет являться решением поставленной задачи.

Предложенный способ хорош всем, кроме одного - неизвестны эффективные алгорифмы построения множества R′. И этот единственный факт лишает практической Ценности весь способ, поскольку описать множество R′ не менее трудно, чем решить исходную целочисленную задачу. Следовательно, надо искать иной путь решения задачи. Непригодный способ состоял в том, что мы пытались сразу отбросить много "ненужных" точек из многоугольника Q (все, которые не входят в R′). Попробуем теперь сделать то же самое, но постепенно.

Заменим решение исходной целочисленной задачи линейного программирования на многоугольнике Q решением ряда задач линейного программирования на многоугольниках Q₁, Q₂, Q₃,... Здесь Q₁=Q. Многоугольники эти таковы, что множество целых точек в них одно и то же. Таким образом, понятно, что если оптимальный план задачи линейного программирования на многоугольнике Q_s удовлетворяет условию целочисленности, то он является и оптимальным целочисленным планом исходной задачи. Процесс решения на этом заканчивается. Если же на многоугольнике Q_s оптимальный план не удовлетворяет условию целочисленности, то происходит переход к Q_s+1 путем добавления одного правильного отсечения (на рис. 15 прямая АВ). Это вновь добавленное неравенство гарантирует, что оптимальный план, в котором не выполнялось условие целочисленности, заведомо не будет даже допустимым планом в последующих задачах. Ну, а множества целых точек это неравенство не сужает. Иными словами, правильные отсечения позволяют выбрасывать заведомо ненужные точки многоугольника ограничений, не теряя при этом нужных точек. Такая идея и лежит в основе метода Гомори. Ему удалось предложить алгорифмический процесс построения правильных отсечений, не использующий ни рисунка, ни каких-либо других интуитивных соображений, что сделало бы его непригодным для решения многомерных задач. Кратко опишем этот алгорифм.

Пусть требуется найти максимум величины

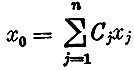
при условиях

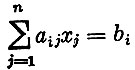
x_j≥0, x_j - целое число.

Обозначим через х оптимальный опорный план этой задачи. Целевую функцию x₀ и все переменные x₁, x₂, x,... x_n можно выразить через небазисные переменные x_j(j∈M), которые соответствуют этому оптимальному плану

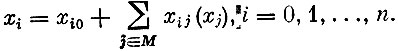
Введем обозначение

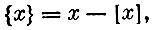
где [x] - целая часть числа x. Понятно, что {x} представляет собой дробную часть числа x.

Это понятие используется для построения правильных отсечений на основе следующего утверждения: если план не удовлетворяет условию целочисленности, то условие

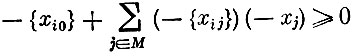
определяет правильное отсечение. Последовательное добавление правильных отсечений к исходной задаче позволяет построить упоминавшиеся ранее многоугольники Q₁, Q₂, Q₃,... P. Гомори доказал конечность такого алгорифма.

Несмотря на всю свою точность, рассмотренный метод имеет довольно ограниченную практическую ценность. Число переходов так велико, что с его помощью, даже используя самую современную вычислительную технику, удается решать только те задачи, которые имеют небольшой объем.

Поэтому для решения задач целочисленного программирования нередко применяются методы комбинаторного анализа. Остановимся здесь на одном из них - методе ветвей и границ. Изложим его применительно к общей задаче дискретного программирования.

Найти

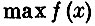
при условии

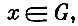
где G - некоторое конечное множество.

Для того чтобы понять идею метода в чистом виде, на минутку отвлечемся от всякой математики и рассмотрим такую ситуацию. Известно, что в мешке с монетами одинакового достоинства имеется одна фальшивая монета, отличающаяся большим весом. Как отыскать фальшивую монету? Можно, конечно, взвешивать одну за другой все монеты. Но это очень долгое дело. Лучше сделать так. Разделим содержимое мешка на две равные части и каждую взвесим, затем более тяжелую часть снова разделим пополам и будем действовать аналогичным образом, пока не доберемся до фальшивой монеты. Таков по сути принцип метода ветвей и границ: деление мешка - ветвление, взвешивание каждой части - определение соответствующих границ.

Перейдем к формальному изложению этого метода. Во многих задачах оказывается возможным определить точную верхнюю границу функции f(x) на множестве всех планов G. Обозначим ее α(G), т. е. f(x)≤α(G) на G Произведем разбиение G на несколько непересекающихся подмножеств G₁, G₂, ..., G_k - ветвление. На каждом из этих подмножеств оценим сверху функцию, т. е. определим числа α(G₁), α(G₂), ..., α(G_k). Если при этом удается найти некоторый план 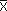∈G_r, для которого выполняются условия

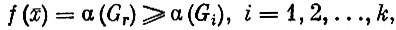
то, как явствует из смысла оценок, 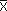- оптимальный план исходной задачи. Если такой план не обнаружен, продолжаем процесс разбиения, начиная его с подмножества с самой высокой оценкой и т. д. Поскольку множество всех планов конечно, то в конце концов оптимальный план будет найден.

Покажем применение этого метода к решению конкретных задач. Как всегда, рассмотрим очень простой пример.

Найти

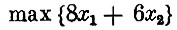
при условиях

(1)

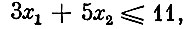
(2)

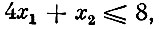
(3)

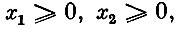
(4) x₁ - целое.

Найдем оценку сверху целевой функции на множестве планов, определяемом условиями (1)-(4). Это легко сделать, отказавшись временно от условия (4). Многоугольник, заданный условиями (1)-(3), на рис. 16 заштрихован.

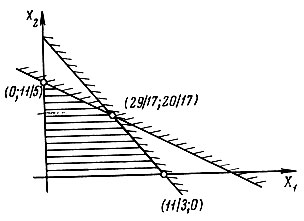
Рис. 16

Как уже говорилось, максимум линейной функции достигается в одной из вершин многоугольника ограничений. Координаты их находятся путем решения совместно соответствующих уравнений прямых. Сравнивая значения целевой функции в вершинах многоугольника ограничений, устанавливаем, что максимум достигается в точке (29/17; 20/17) и, стало быть,

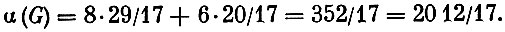
Понятно, что не существует плана, удовлетворяющего условию (4), на котором бы эта оценка достигалась. Поэтому разбиваем множество допустимых планов G на две части: одна из них - G₁ содержит те допустимые планы, у которых x₁≤1, во вторую - G₂ входят допустимые планы с x₁≥2. Важно отметить, что при этом не потеряно ни одного допустимого плана.

Определим оценки целевой функции на таких множествах. Для этого придется решить две задачи линейного программирования.

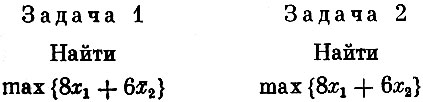
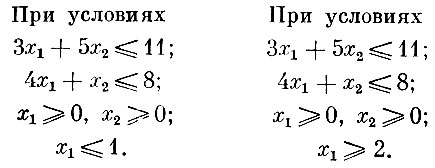
Многоугольник допустимых планов задачи 1 изображен на рис. 17. Максимум достигается в точке (1; 8/5), и, следовательно,

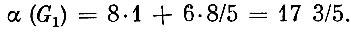
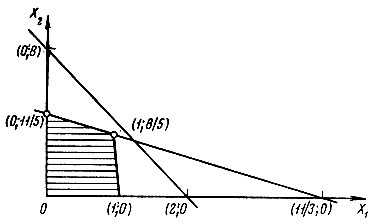
Рис. 17

Для задачи 2 многоугольник допустимых планов вырождается в единственную точку (2,0) и, очевидно,

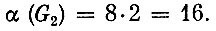
Окончательно пришли к такому результату. Имеется допустимый план (1; 8/5), для которого выполняются условия

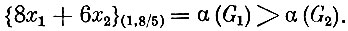
По сказанному выше план (1; 8/5) является оптимальным. Задача решена.