2. Нелинейное программирование

Модифицируем задачу размещения, которая была рассмотрена во второй главе этой книги. Примем, что в этой задаче производственные затраты на единицу продукции не являются постоянными и, следовательно, производственные затраты не пропорциональны объему выпуска, а зависят от него нелинейно, т. е. функция f_i(x_i), представляющая затраты на производство продукта в объеме x_i на i-м предприятии, может быть нелинейной. Производственные мощности будем считать любыми, а не обязательно принадлежащими множеству целочисленных значений. Делая такие предположения, приходим к следующей математической задаче.

Найти

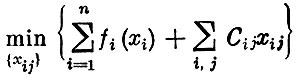
(минимум суммарных затрат на производство и транспортировку) при условиях

(1) 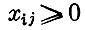(перевозятся неотрицательные количества продукта);

(2) 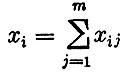(произведенные количества продукта полностью доставляются потребителям);

(3) 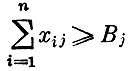(каждый пункт потребления получает не меньше заданного в нем объема потребления).

Экстремальные задачи, в которых либо ограничения, либо целевая функция, либо и то и другое нелинейны, называются задачами нелинейного программирования (в нашей задаче нелинейна целевая функция). К сожалению, пока не имеется общих методов, подобных методу последовательного улучшения плана или симплекс-методу в линейном программировании, которые позволяли бы решать любые задачи нелинейного программирования. Поэтому здесь будут указаны возможности решения лишь для некоторых, впрочем, весьма важных частных случаев.

Только сначала выясним, в чем выражается "неприятный эффект" нелинейности. Для этого сопоставим задачи линейного и нелинейного программирования. Рассмотрим, как выглядит в них множество допустимых планов. В задачах линейного программирования оно выпуклое, с конечным числом крайних точек (напоминаем, что крайней точкой называется всякая точка множества, которая не является внутренней ни для какого отрезка, целиком принадлежащего этому множеству). Это сразу становится понятным, если вспомнить, что границами множества служат гиперплоскости. В задачах же нелинейного программирования (в том случае, когда нелинейны ограничения) множество допустимых планов может быть невыпуклым, может иметь бесконечное число крайних точек.

Например, пусть допустимая область на плоскости XOY определяется ограничениями (X-1)²+(Y-1)²≤1; YX≤1. На рис. 8 видно, что эта область невыпуклая (отрезок, соединяющий любые две точки на гиперболе, не принадлежит этой области). Кроме того, все точки, лежащие на ограничивающей область дуге окружности, являются крайними, т. е. имеется бесчисленное множество крайних точек.

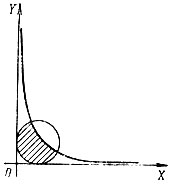
Рис. 8

В том случае, когда нелинейна целевая функция, возникают другие затруднения. В первой главе было указано, что решение задачи линейного программирования обязательно находится в некоторых (возможно, в нескольких) крайних точках множества допустимых планов. Но при нелинейной целевой функции экстремум может достигаться не только на границе, но и внутри допустимой области (рис. 9).

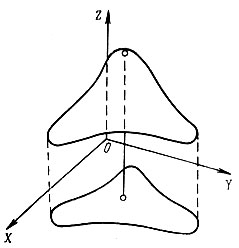
Рис. 9

И еще один осложняющий момент, который отличает нелинейные задачи от линейных. Целевая функция в допустимой области может иметь несколько локальных экстремумов, тогда как в линейной задаче локальный максимум или минимум обязательно является и глобальным (рис. 10). Здесь надо иметь в виду, что функция имеет в точке А локальный экстремум, если значения функции в точке А не больше (или не меньше), чем значения функции во всех достаточно близких к А точках. Если же значение функции в точке А не больше (не меньше), чем значение ее в любой точке допустимой области, то в точке А имеется глобальный экстремум.

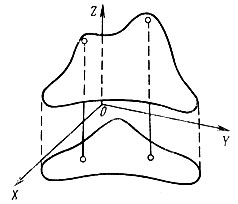
Рис. 10

Перечислив основные отличия нелинейных задач по сравнению с линейными, укажем некоторые возможные пути их решения.

Начнем с рассмотрения простейших задач, для решения которых иногда даже не нужны методы математического программирования. Пусть, например, требуется найти максимум функции y=-х²+8х-14 при условии х∈[0,10]. Из классического анализа известно, что наибольшее значение дифференцируемой функции может достигаться либо на концах промежутка, т. е. при х=0 или х=10, либо в той внутренней точке, где производная функции обращается в нуль. Таким образом, равенство нулю производной есть необходимое условие того, что экстремум достигается во внутренней точке промежутка. Если в рассматриваемой задаче вычислить производную и приравнять ее нулю, т. е. y′= -2х+8=0, легко найти, что х=4. Если максимум достигается внутри промежутка, то только при х=4. Соответствующее значение функции y(4)=2. Вычислим теперь значения функции на концах промежутка: y(0)=-14 и y(10)=-34. Так как где-то функция имеет максимальное значение, то очевидно, что максимум достигается при х=4. Задача решена.

Проанализируем теперь причины, обусловившие возможность столь легкого решения. Во-первых, функция зависит от одной переменной; во-вторых, функция дифференцируема всюду в промежутке [0, 10]; и, в-третьих, функция задана очень простым аналитическим выражением, благодаря чему уравнение для отыскания корня производной также оказывается совсем несложным. Если бы не эти обстоятельства, то аналогичная задача могла бы стать чрезвычайно трудоемкой. К сожалению, именно такими (зависящими от многих переменных, непросто заданными и т. п.) бывают очень многие практические задачи. Поэтому классический анализ к ним неприменим, нужны более тонкие методы математического программирования.

При решении задачи математического программирования (как многомерной, так и одномерной, линейной и нелинейной) представляются возможными два направления. Первое из них - прямые методы нахождение экстремума, связанные с последовательным вычислением функции в некоторых точках области ее задания. Другое направление - это нахождение необходимых (или необходимых и достаточных) условий, которым должны удовлетворять координаты точки, доставляющей экстремум. Однако указанные направления не исключают друг друга и совместное использование методов того и другого типа весьма эффективно.

Так, в линейном программировании поочередное использование прямых методов и проверки необходимых условий оптимальности составляет суть описанных выше способов последовательного улучшения плана, симплекс-метода и др. В нелинейном программировании пока еще не созданы столь универсальные способы решения задач. Конечный алгорифм имеется лишь для задачи квадратичного программирования, т. е. задачи с линейными ограничениями и целевой функцией, задаваемой полиномом второй степени. Поэтому, рассматривая общую задачу нелинейного программирования, приходится демонстрировать по отдельности методы первого и методы второго направления.

Начнем с первого направления. Здесь наиболее широко применяются для решения нелинейных задач различные итеративные методы, основанные на достаточно простой идее - пошаговом приближении к точке экстремума. Если известно заранее, что целевая функция имеет единственный минимум, то поиск точки, в которой он достигается, может быть организован так. Возьмем в качестве начальной произвольную точку допустимой области и определим для этой точки то направление, в котором функция убывает с наибольшей скоростью. Сделав небольшой "шаг" в этом направлении, перейдем к новой точке. Потом снова отыскиваем наилучшее направление для перехода к очередной точке и т. д. Разумеется, это только схематическое описание общей идеи одного из итерационных процессов. Практически же нужно обоснованно выбирать величину шага, количество необходимых шагов, видоизменять поиск экстремальной точки при выходе на границу допустимой области и т. д.

Если целевая функция имеет несколько локальных минимумов или просто заранее о ней ничего не известно, то поиск экстремальной точки еще более осложняется. Это объясняется тем, что описанный процесс улучшения плана может в этом случае привести к локальному минимуму, очень далекому от глобального. Чтобы избежать такого осложнения, приходится, завершая один поиск, начинать его снова, но уже с другой начальной точки. Проделав процедуры подобного рода с различными (желательно многими) точками, можно выбрать в качестве приближенного решения задачи наименьший из полученных локальных минимумов (см. рис. 10). Чем большее число точек и районов допустимой области просмотрено, тем больше шансов, что найденный результат представляет действительное решение задачи.

Наряду с итеративными способами решения задач нелинейного программирования нередко предлагаются и другие методы. Один из них указан в 1964 г. вьетнамским математиком Хоанг Туем. Его подход основан на идее сужения допустимой области за счет отбрасывания тех частей, в которых заведомо не достигается экстремум.

В тех случаях, когда нелинейная задача обладает какой-либо специальной структурой, нередко удается использовать эту специфику при решении. Особенно важный специальный вид таких задач можно проиллюстрировать на упоминавшейся уже задаче размещения из второй главы.

Для некоторых видов производства, таких, например, как эксплуатация месторождений полезных ископаемых, представляется естественным допущение о выпуклости функции производственных затрат (экономически это означает, что затраты на единицу продукции возрастают с объемом добычи)^*. Множество допустимых планов, определяемое условиями (1)-(3) рассматриваемой задачи, представляет собой выпуклый многогранник. В задаче требуется найти минимум выпуклой функции, заданной в выпуклой области. Этот класс задач носит название выпуклого программирования.

^* (Напомним, что функция называется выпуклой, если для любой пары точек x₁ и x₂ из области ее определения (которая предполагается выпуклой) и для всех чисел λ, 0≤λ≤1 выполняется неравенство f(λx₁+(1-λ)x₂)≤λf(x₁)+(1-λ)f(x₂). График такой функция изображен на рис. 11.)

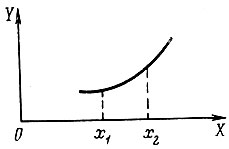
Рис. 11

Доказано, что минимум выпуклой функции на выпуклом множестве точек может быть только один и, следовательно, локальный минимум совпадает с глобальным минимумом. В этом случае возможно сколь угодно точно аппроксимировать (заменять) задачу выпуклого программирования задачей линейного программирования. Для такой аппроксимации в данной задаче нужно заменить кривые f_i(x_i) вписанными в них ломаными линиями (рис. 12), а затем преобразовать целевую функцию в линейную, используя уравнения звеньев этих ломаных линий и вводя дополнительные ограничения. Полученная при этом задача линейного программирования имеет точное решение, которое одновременно является приближенным ответом для исходной нелинейной задачи. Разумеется, точность такого ответа будет тем выше, чем точнее кривая аппроксимирована ломаными прямыми линиями.

Рис. 12

Аппроксимация кривой линии некоторым числом ломаных прямых в рассматриваемой задаче размещения экономически соответствует замене одного нелинейно описываемого способа производства продукта на данном предприятии рядом способов производства (скажем, первой тысячи изделий, второй тысячи и т. д.), единообразно описываемых линейно, но с различными затратами. Получаемый при решении такой линейно-программной задачи план и представляет приближенное решение нелинейной задачи.

Нужно иметь в виду, что изложенный метод неприменим при отсутствии условия выпуклости функции. В этом случае в план может попасть, например, выпуск третьей тысячи изделий, а выпуск первых двух тысяч не попадет в него. Иначе говоря, план будет нереальным. В случае выпуклости такого не произойдет: выпуск первых тысяч изделий как более выгодный обязательно войдет в план. Мы сделали это замечание, поскольку, к сожалению, гипотеза о выпуклости функций очень часто оказывается неправомерной. Для большинства видов производства затраты на выпуск единицы продукции обычно уменьшаются с ростом производственных мощностей, т. е. функции f_i(x_i) монотонно возрастают и вогнуты - снова общая задача нелинейного программирования.

Обратимся теперь к другому направлению - нахождению необходимых (или необходимых и достаточных) условий, которым должны удовлетворять координаты точки, являющейся решением задачи нелинейного программирования. Как всегда, для иллюстрации выберем простейший случай.

Найти максимум функции

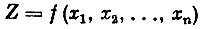
при условиях

(1)

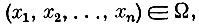
(2)

Всякой точке (x₁, x₂, ..., x_n) из множества Ω можно сопоставить два числа z=f(x₁, x₂, ..., x_n) и y=g(x₁, x₂, ..., x_n). Допустим для простоты, что все множество Ω отображается таким образом в выпуклое множество на плоскости YOZ (рис. 13). Понятно, что решение исходной задачи геометрически изображается точкой на границе полученного выпуклого множества S.

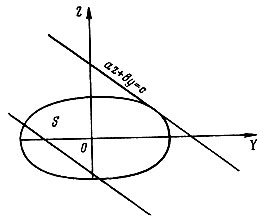
Рис. 13

Покажем, как найти граничные точки множества S. На плоскости YOZ проведем прямую az+by=c и станем перемещать ее параллельно самой себе до тех пор, пока она не станет касательной к выпуклому множеству S. Точки касания совпадают с граничными точками множества. Если проделать эту операцию с прямыми всевозможных направлений, то удается получить всю границу множества S. Попробуем аналитически охарактеризовать точки касания. Легко заметить, что на рис. 13 среди всех прямых данного направления прямая az+by=c, являющаяся касательной к множеству 5, обладает таким свойством - расстояние от начала координат до касательной экстремально по сравнению с расстояниями до других прямых этого направления, имеющих общие точки с S.

Так как при фиксированных a и b расстояние от прямой до начала координат пропорционально с, приходим к следующей задаче: максимизировать величину az+by =af(x₁, ..., x_n)+bg(x₁, ..., x_n). При a≠0 возникает эквивалентная задача: максимизировать величину f(x₁, ..., x_n)+λg(x1, ..., x_n), где λ=b/a. Таким образом исходную экстремальную задачу с ограничением можно свести к экстремальной задаче, но без ограничений и отысканию одного параметра - множителя λ (понятно, что аналогичный прием может быть использован и при наличии нескольких ограничений). Вновь построенная функция называется функцией Лагранжа, величина λ, носит название множителя Лагранжа, а сам процесс сведения условной экстремальной задачи к безусловной задаче есть метод множителей Лагранжа.

Множитель Лагранжа имеет прозрачный экономический смысл. Если под f(x₁, ..., x_n) понимать "доход", соответствующий плану (x₁, x₂, ..., x_n), а под g(x₁, x₂, ..., x_n) - "издержки ресурса", соответствующие тому же плану, то величина λ имеет смысл цены (оценки) этого ресурса. Можно доказать, что если рассматривать экстремум при переменном ограничении (g≤ m), то производная экстремального значения функции f по величине ограничения с точностью до знака равна множителю Лагранжа. Иначе говоря, множитель Лагранжа характеризует скорость изменения экстремального значения целевой функции в зависимости от размера ресурса. Эта величина носит название маргинальной оценки.

Перейдем к описанию общей задачи нелинейного программирования.

Найти

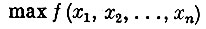
при условиях

(1)

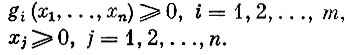
Построим для этой задачи функцию Лагранжа

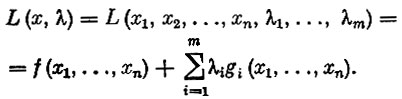
Можно доказать, что вектор x является решением задачи тогда, когда существует такой вектор 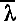, с неотрицательными компонентами, что справедливы неравенства

(2)

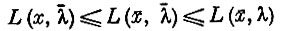
при всех допустимых векторах x и неотрицательных векторах λ. Пара векторов (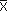, 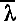) называется в этом случае седловой точкой функции L (x, λ). Такое "лошадиное" название связано с тем, что графически (см. рис. 14) функция L (x, λ) в окрестности точки (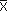, 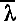) выглядит подобно седлу. Значение этой точки очень велико. Она облегчает поиск максимума целевой функции нелинейной задачи.

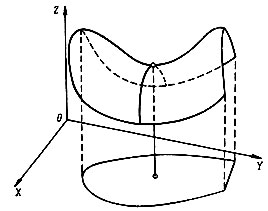
Рис. 14

Между решением общей задачи нелинейного программирования и седловой точкой функции Лагранжа существует тесная связь. Для известного оптимального вектора 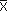можно при некоторых естественных предположениях подобрать такой вектор 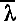, чтобы пара векторов (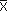, 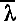) являлась седловой точкой функции L(x, λ). Этот факт утверждается известной теоремой Куна и Таккера: вектор 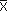является оптимальным вектором нелинейной задачи тогда и только тогда, когда существует такой вектор 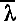≥0, что пара (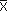, 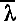) есть седловая точка функции L(x, λ). Значит, вместо того, чтобы специально решать задачу нелинейного программирования, можно (что зачастую проще) искать седловую точку функции Лагранжа L(x, λ). Зная ее, мы будем знать и решение задачи^*. Не будем утомлять читателей-экономистов доказательством этого факта, а ограничимся его экономической интерпретацией.

^* (Тот Факт, что всякую задачу нелинейного программирования можно свести к задаче поиска седловой точки соответствующей функции Лагранжа, позволяет также проверить на оптимальность каждый допустимый план 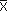нелинейной задачи: если удастся для него найти такой вектор 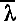≥0, что пара (x̃, λ̃) является седловой точкой функции L (x, λ), то план 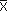оптимален; если такого вектора λ̃≥0 не существует, то план не оптимален.)

Ограничения общей задачи нелинейного программирования очень часто имеют такой вид:

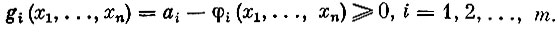
Постоянный вектор a=(a₁, a₂, ..., a_m) может интерпретироваться как наличие производственных ресурсов, а функции φ_i - как затраты этих ресурсов при выбранном плане x=(x₁, ..., x_n). Таким образом, величина g_i(x₁, ..., x_n) с экономической точки зрения означает количество неиспользованного i-го ресурса при выбранном производственном плане x=(x₁, ..., x_n). Функция f(x₁, ..., x_n) выражает доход предприятия, соответствующий плану x.

Функцию Лагранжа в этой задаче можно интерпретировать как ценностное выражение результата производства, состоящего в получении дохода и сохранении неиспользованных ресурсов, а множители Лагранжа являются здесь оценками единицы неиспользованных ресурсов разных видов. Экономический смысл седловой точки у функции Лагранжа состоит в том, что между оценками, ценами имеющихся ресурсов и величиной дохода имеется равновесие, отклоняться от которого не выгодно ни при управлении производственным процессом, ни при назначении цены на ресурсы.

Приведем еще одну экономическую задачу, которая сводится к задаче нелинейного программирования. Планируя потребление, нередко приходится использовать функцию, выражающую объем спроса на некоторый продукт в зависимости от его цены. Так как при значительном снижении цены спрос увеличивается в меньшей степени, очевидно, что эта функция нелинейна. Если требуется рассчитать план производства продукта и связанные с ним цены таким образом, чтобы объем потребления был согласован с этими ценами, а эффект от производства и потребления продукта достиг максимума, то подобная постановка приведет к типичной задаче нелинейного программирования.

Интересно сравнить роль оценок в задачах линейного и нелинейного программирования. В линейном программировании оценки оптимального плана обладают тем свойством, что исчисленные по ним затраты совпадают с оценкой получаемого "эффекта". Иначе обстоит дело в нелинейном программировании. Необходимое условие достижения оптимума состоит здесь в равенстве лишь приростных, дифференциальных затрат и "маргинального (предельного) эффекта". Знание этих величин позволяет определить, являются ли желательными те или иные изменения плана, что особенно важно при анализе эффективности отдельных мероприятий с точки зрения народнохозяйственных задач. Однако двойственное решение, одновременно устанавливающее и оптимальные затраты и оптимальный доход, в нелинейном программировании не достигается. Например, в задаче размещения, приведенной в начале этого параграфа, при нелинейной (вогнутой) функции затрат оценка продукта может оказаться ниже средних затрат на единицу продукта. Рекомендуем читателю вернуться к этой экономической интерпретации после того, как им будет прочтена пятая глава.

Несмотря на большие трудности, связанные с решением задач нелинейного программирования, в настоящее время интенсивно ведется работа по созданию новых и совершенствованию уже известных методов их решения. Это результат большой практической важности задач такого типа, их актуальности.