1. Динамическое программирование

Многошаговые процессы принятия решений начали изучаться где-то в начале 50-х годов. Для этого хотя и не очень широкого, но часто встречающегося класса задач далеко не всегда пригодны методы классического математического анализа, аппарат линейного программирования или вариационное исчисление. Специальные же методы, предназначенные для исследования таких процессов, требовали разработки специальной концепции. Такая концепция, получившая название динамического программирования, была создана американским математиком Р. Беллманом и его школой. Существенный вклад в развитие методов динамического программирования сделан советскими математиками.

Прежде чем дать общее описание сущности этой концепции, как обычно, начнем с очень простой задачи, которая тем не менее позволит познакомиться с характерными чертами динамического программирования. Пусть требуется погрузить в самолет грузоподъемностью W груз, состоящий из предметов N различных типов таким образом, чтобы стоимость всего груза оказалась максимальной.

Введем следующие обозначения: P_i - вес одного предмета i-го типа; V_i - стоимость предмета i-го типа; x_i - число предметов i-го типа, загружаемых в самолет. После чего поставим вопрос о подборе для самолета допустимого груза максимальной ценности. В результате приходим к следующей экстремальной задаче.

Найти 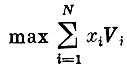(ценность груза)

при условиях

(1) 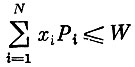(вес груза не превышает грузоподъемности самолета);

(2) 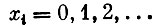(предметы неделимы).

Если бы не второе условие, поставленная задача решалась бы уже хорошо знакомыми нам методами линейного программирования. Наличие же такого условия делает методы линейного программирования неприменимыми (подробнее об этом см. § 3 настоящей главы).

Для того чтобы лучше понять схему решения, опишем ее в терминах рассматриваемой задачи, т. е. на языке "загрузки самолета". Вначале загрузим самолет только предметами первого типа. Тогда максимальная стоимость груза (обозначим ее f₁(W)) определится как

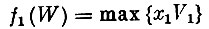
при условиях

(1′)

(2)

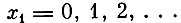
Так как x₁≤W/P₁, а для нахождения максимума нужно x₁ взять возможно большим, то сразу ясно, что x₁=[W/P₁] и f₁(W)=[W/P₁]V₁. График этой функции - ступенчатая линия (пунктирная линия на рис. 7)^*.

^* (Выражение 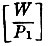обозначает наибольшее целое число, не превосходящее )

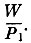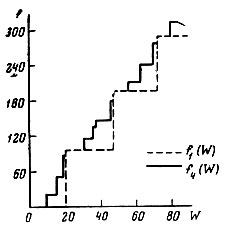
Рис. 7

Итак, мы знаем, чему равна максимальная стоимость груза, если вся грузоподъемность W расходуется на груз первого типа, т. е. для этого случая построена решающая функция f₁(W), дающая максимальную стоимость при грузоподъемности W.

Рассмотрим теперь, что получится, если загрузить самолет предметами первого и второго типов. В этом случае максимальная стоимость загрузки обозначается через f₂(W). Если предметов второго типа взято х₂, то самолет может взять предметов первого типа по весу не более чем W - х₂Р₂. Из сказанного выше следует, что максимальная стоимость их равна f₁(W-x₂P₂), а общая стоимость груза в этом варианте будет x₂V₂+f₁(W-x₂P₂). Остается определить x₂. Ясно, что величина f₂(W) - максимальная стоимость груза, состоящего из предметов первого и второго типов, - определяется как максимум для всех возможных вариантов выбора x₂, т. е.

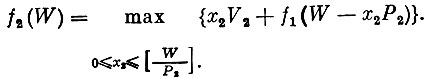
Продолжая действовать аналогично, т. е. всякий раз к уже имеющимся добавляя предметы еще одного типа, через N шагов придем к такому соотношению:

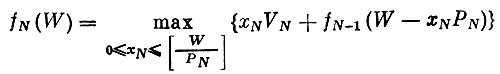
(максимальная стоимость груза, состоящего из предметов N типов),

(стоимость взятых предметов N-типа),

(максимальная стоимость груза, состоящего из предметов (N-1) типов с общим весом не более W-x_NP_N).

Из полученных рекуррентных соотношений без большого труда могут быть последовательно найдены функции f₁(W), f₂(W), ..., f_N(W), а вместе с ними полное решение поставленной задачи.

Это решение поясним на числовом примере. Пусть W=83, а веса и стоимости предметов равны соответственно P₁=24, P₂=22, Р₃=16, P₄=10, V₁=96, V₂=85, V₃=50, V₄=20.

Так как функции f_k(W) потребуются нам для различных значений W (вычисляя f_k(W), нужно знать f_k-1(W-x_kP_k), будем вычислять их последовательно одну за другой при различных значениях W, фиксируя при построении f_k(W) число предметов k-го типа, погружаемых в самолет. Результаты этих вычислений сведены в табл. 22-25. Они содержат значения f₁ (табл. 22), f₂ (табл. 23), f₃ (табл. 24) и f₄ (табл. 25). Экономический смысл этих таблиц легко понять, если иметь в виду, что, например, первая строка табл. 22 означает: при грузоподъемности самолета 48-71 единиц груза он загружается двумя предметами первого типа, стоимость которых 192 денежные единицы.

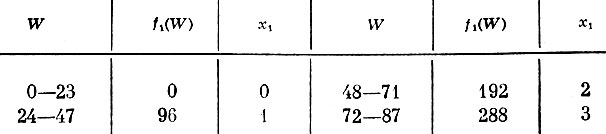
Таблица 22

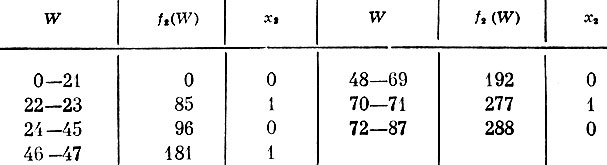
Таблица 23

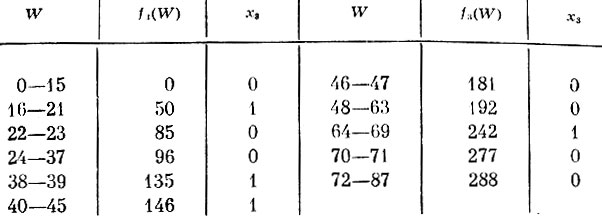
Таблица 24

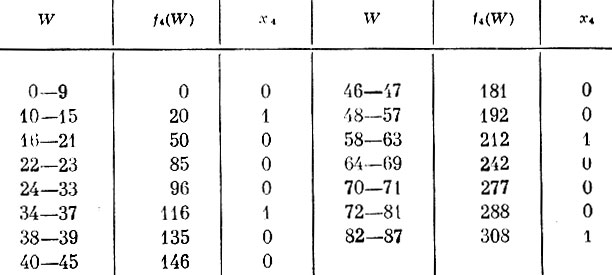
Таблица 25

На основании данных табл. 22-25 нетрудно найти оптимальный план загрузки самолета грузоподъемностью W=83. Из табл. 25 находим, что максимальная стоимость груза f₄ (83) оказывается равной 308, а предметов четвертого типа следует погрузить всего один, так как x₄=1. Этот один предмет имеет вес 10, и, следовательно, предметов остальных типов можно загрузить лишь в пределах веса 83-10=73. Из табл. 24 и 23 последовательно находим, что для W=73 не следует грузить ни предметов третьего типа, ни предметов второго типа, т. е. х₃=0 и х₂=0. Из табл. 22 видно, что при W=73 следует взять три предмета первого типа, т. е. х₁=3. Окончательно наилучший план загрузки таков: следует взять 3 предмета первого типа и 1 предмет четвертого типа. Их суммарная стоимость составляет 308.

По поводу только что рассмотренного примера надо сделать два замечания. Во-первых, удалось не только решить поставленную задачу (найти план загрузки самолета грузоподъемностью W=83), но сделать гораздо больше. Из табл. 22-25 могут быть найдены оптимальные планы загрузки для самолетов любой грузоподъемности в пределах до 87, т. е. вместо одной задачи решен целый набор сходных между собой задач. Это характерная черта метода динамического программирования - расширив задачу, мы облегчили ее решение! Отметим также, что, поскольку метод носит явно выраженный алгорифмический характер, он легко реализуется на ЭВМ.

Вместе с тем нельзя обойти молчанием и одну принципиальную трудность, с которой приходится сталкиваться при решении задач динамического программирования. Дело в том, что для отыскания оптимального решения необходимо хранить в памяти машины обширную информацию обо всех принимаемых решениях вплоть до последнего шага (хранить таблицы типа 22-25). Если количество этих шагов велико, то необходимая информация может даже не поместиться в памяти машины. Для преодоления отмеченной трудности можно предложить такую идею - часть необходимой информации не запоминать, а перевычислять в тот момент, когда в ней возникает необходимость, иначе говоря, экономить машинную память ценой затраты дополнительного машинного времени.

Во-вторых, возможна другая интерпретация рассмотренной задачи. Стержень длиной 83 ед. нужно раскроить на такие заготовки: l₁=24, l₂=22, l₃=16, l₄=10; оценки заготовок равны соответственно V₁=96, V₂=85, V₃=50, V₄=20; требуется, чтобы суммарная оценка полученных заготовок оказалась наибольшей. Для решения подобной задачи, не опираясь на динамическое программирование, в свое время был применен метод, аналогичный вышеописанному. Сочетая метод динамического программирования с линейным программированием, можно добиться полной автоматизации решения задачи о раскрое.

Задача о загрузке самолета играла чисто иллюстративную роль, поясняя главные принципы динамического программирования. Вообще же имеется очень много практически важных задач, которые ставятся и решаются как задачи динамического программирования. Вот одна из них.

Для производства определенного продукта предполагается построить несколько предприятий. Считаются известными: суммарная производственная мощность этих предприятий, наибольшая и наименьшая производственные мощности каждого предприятия, известна также зависимость себестоимости продукции на каждом предприятии от его производственной мощности. Требуется так выбрать производственные мощности предприятий, чтобы суммарная себестоимость производства продукции была минимальной. В этой задаче в роли ресурса выступает суммарная производственная мощность, а в роли способов его использования - выбор тех или иных производственных мощностей для каждого предприятия.

Перейдем теперь к более общему описанию многошаговых процессов принятия решений. Возьмем задачу распределения ресурсов, состоящую в следующем: имеется некоторое количество ресурса х, которое можно использовать N различными способами. Ресурсы и способы могут быть самой различной природы (например, в рассмотренной задаче ресурсом являлась грузоподъемность самолета, а способами использования были загрузки его различными типами предметов).

Если обозначить через х_i количество ресурса, используемое i-м способом, то каждому способу сопоставляется функция полезности φ_i(x_i), выражающая доход от этого способа (в рассмотренной задаче эта функция была представлена величиной V_i[x_i/P_i]). Предполагается, что все доходы измеряются в одинаковых единицах и общий до ход равен сумме доходов, полученных от использования каждого способа.

Теперь можно поставить задачу в математической форме.

Найти

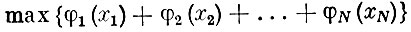
(общий доход от использования ресурсов всеми способами) при условиях

(1) 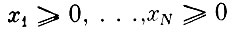(выделяемые количества ресурсов неотрицательны);

(2) 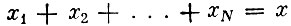(общее количество ресурсов равно x).

Для этой общей задачи могут быть построены рекуррентные соотношения

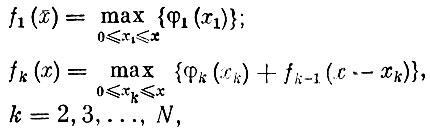
с помощью которых находится ее решение.

При выводе этих рекуррентных соотношений по сути использовался следующий очевидный принцип: оптимальная стратегия обладает тем свойством, что для любого первоначального состояния после некоторого начального этапа решения совокупность последующих решений должна составлять оптимальную стратегию по отношению к состоянию, к которому пришли в результате начального этапа решения. Этот принцип, получивший название принципа оптимальности, лежит в основе всей концепции динамического программирования. Именно благодаря ему удается при последующих переходах испытывать не все возможные варианты, а лишь оптимальные выходы. Рекуррентные соотношения позволяют заменить чрезвычайно трудоемкое вычисление максимума по N переменным в исходной задаче решением N задач, в каждой из которых максимум находится лишь по одной переменной. С их помощью могут быть решены задачи, которые иными путями решать не удается.

Все предшествующие рассуждения имели в виду задачу с одним ресурсом. Но та же идея анализа задачи, основанная на принципе оптимальности, может быть использована и в случаях, когда ресурсов несколько. Однако с увеличением размерности объем вычислений быстро растет и требования к памяти ЭВМ столь возрастают, что реально метод динамического программирования непосредственно может быть применен к задачам, включающим не больше 3-4 видов ресурсов. Это отличает его от линейного программирования, где преодолимы и много большие размерности.

Отметим, что метод динамического программирования широко используется и в задачах автоматического регулирования. Этот же круг задач успешно исследуется на основе принципа максимума, разработанного советским ученым акад. Л. С. Понтрягиным (см. приложение).