3. Модель размещения сельскохозяйственного производства

Одной из наиболее плодотворных и перспективных областей применения оптимального и, в частности, линейного программирования является сельское хозяйство. Здесь математико-экономические методы могут в сравнительно короткий срок дать очень большой эффект. С одной стороны, сельскохозяйственные предприятия и производственные процессы в них отличаются значительной однородностью. Они выпускают намного меньший ассортимент продукции, используя при этом менее разнообразные средства производства, чем промышленность. С другой стороны, решение задач планирования в сельском хозяйстве зачастую оказывается сложнее, нежели в промышленности, так как здесь приходится учитывать природные условия, сезонность работ, стохастический (случайный) характер некоторых величин и др. Как это ни парадоксально, но именно эти осложняющие факторы усиливают эффективность применения методов оптимального планирования. Без таких методов оказывается просто невозможно научно обоснованно решить многие экономические проблемы развития сельского хозяйства.

Рассмотрим простейшую модель размещения сельскохозяйственного производства. Имеется m видов земельных участков, качественно отличающихся друг от друга. Хозяйство планирует возделывание n видов культур, причем полученная продукция должна находиться в соотношении l₁:l₂: ...: l_n. Предполагаются известными числа a_ij, показывающие, сколько центнеров продукции j-й культуры можно получить с i-то участка. Требуется определить, какую часть каждого участка под какую культуру нужно отвести, чтобы получить максимальное число ассортиментных наборов продукции. Обозначая через x_ij долю i-го участка, отводимую под j-ю культуру, приходим к следующей задаче.

Найти величины x_ij из условий

(1)

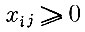
(доля участка не может быть отрицательной);

(2)

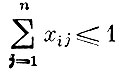
(сумма долей i-го участка, отводимых под различные культуры, не превышает единицы);

(3)

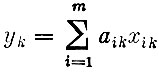
(объем продукции k-й культуры, полученной на всех участках);

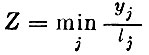
(число ассортиментных наборов продуктов);

Z - достигает максимума.

Нетрудно заметить, что мы пришли к той же самой модели, что и в задаче о выборе производственной программы. Здесь снова проявилась замечательная особенность математики, с которой мы уже неоднократно сталкивались, - одна и та же математическая модель описывает совершенно различные явления. В качестве полезного упражнения можно порекомендовать читателю "перевести на сельскохозяйственный язык" иллюстративный пример из предыдущего параграфа.

Если рассматривать задачу размещения сельскохозяйственного производства более полно, учитывая урожайность в течение ряда лет, влияние севооборотов, возможность искусственного орошения отдельных участков и т. п., то соответствующие математические модели будут более сложными. Еще сложнее модели, где различные отрасли сельскохозяйственного производства рассматриваются в комплексе. Тем не менее все эти модели остаются, как правило, в рамках линейного программирования независимо от того, в каких масштабах они применяются - от бригады и хозяйства до республики и всей страны.

Для решения проблем сельскохозяйственного производства используются и другие модели. Упомянем, в частности, задачи об оптимальной структуре тракторного парка, о выборе рационов откорма сельскохозяйственных животных, о наилучшей системе внесения удобрений в почву и др. При решении подобных проблем, если оно требует значительного приближения модели к действительности, например учета погодных факторов, возможного спроса на сельскохозяйственную продукцию и т. п., модель перестает быть линейно-программной, и для ее исследования требуется другой математический аппарат. Этот вопрос будет рассматриваться в следующей главе.

В качестве примера практического применения математических методов в планировании сельскохозяйственного производства укажем расчеты, проведенные для совхозов "Семеновод" и "Бийский" Алтайского края с участием математико-экономического отдела Института математики СО АН СССР. В результате этих расчетов были найдены планы размещения сельскохозяйственных культур, а также разработаны наиболее выгодные виды специализации для каждого хозяйства. Проводились также расчеты рационального размещения сельскохозяйственного производства по зонам Новосибирской и Омской областей. Разработки комплекса моделей для страны в целом проводятся Институтом кибернетики Министерства сельского хозяйства и другими организациями.

Несколько слов об экономическом смысле оценок для задачи о размещении сельскохозяйственного производства. Подобно прокатным оценкам, здесь получаются оценки различных участков земли, позволяющие соизмерять и сопоставлять затраты, возникающие при производстве одной и той же продукции на землях разного качества. На базе этих оценок может быть обоснованно исчислена рента на землю различных по качеству участков, которая в вопросах планирования сельскохозяйственного производства имеет не меньшее значение, чем оценка производственных фондов в промышленности.

Учет ренты на землю в цене продукции позволяет прежде всего экономически уравнять условия производства для различных районов. Действительно, только рентные отчисления могут позволить получить равную оценку результатов при равном труде в хозяйствах, расположенных на Северном Кавказе и в Коми АССР. Кроме того, взимание ренты, учитывающей разнообразие различных территорий, стимулирует рациональное использование лесов, охотничьих угодий, водоемов, служит экономическим рычагом, предотвращающим бесхозяйственное отношение к этим природным богатствам. Экономически грамотное использование минеральных богатств земли - руд, угля, нефти, газа - обеспечивается с помощью горной ренты.

Высказанные выше общие положения о планировании сельскохозяйственного производства проиллюстрируем конкретным числовым примером.

Пусть имеется три участка различной по плодородию земли - лучшей, среднего качества и худшей. Площадь последнего будем считать практически неограниченной. По плановому заданию на этих участках нужно произвести 5000 ц пшеницы, 3500 ц ржи и 5000 ц овса. Требуется составить такой план, который обеспечил бы выполнение задания с минимальными затратами труда. Данные об урожайностях и затратах труда на каждую культуру (в них включены и прочие затраты) приведены в табл. 14.

Таблица 14

Прежде чем строить оптимальный план посева, проведем анализ имеющихся данных. Выясним, каким образом целесообразнее всего использовать лучшую землю. Легко подсчитать, что гектар лучшей земли, отведенной под пшеницу, дает такой же урожай, как 1,5 га земли среднего качества. Следовательно, использование 1 га лучшей земли под пшеницу, требующее 10 дней труда, дает ту же продукцию, что и 15 дней труда на земле среднего качества и, значит, лучшая земля обеспечивает экономию труда в размере пяти дней. Для ржи вместо гектара лучшей земли нужно использовать ⁵/₄ га земли среднего качества, а экономия от использования лучшей земли составляет ¹/₄·8=2 дня. Для овса вместо 1 га лучшей земли требуется 14/13 га земли среднего качества, а экономия от использования лучшей земли составляет 1/13·7=0,54 дня. Отсюда ясно, что наиболее эффективно можно уменьшить затраты труда, если под пшеницу использовать лучшую землю.

Итак, отведем всю лучшую землю под пшеницу, что даст в результате 3000 ц. Но ведь плановое задание требует еще 2000 ц пшеницы. Какую землю следует использовать для их получения? Подсчеты, аналогичные предыдущим, показывают, что под пшеницу нужно отвести еще 100 га земли среднего качества (земля среднего качества по сравнению с худшей дает экономию в 3,3 дня на гектар пшеницы, тогда как для ржи и овса экономия составляет соответственно 2,67 дня и 0,28 дня). В точности такие же рассуждения позволяют заключить, что под рожь следует отвести оставшиеся 100 га земли среднего качества и еще 100 га худшей земли. При этом урожай ее составит 100·20+15·100=3500 ц. Плановое задание по производству овса можно выполнить, если отвести под него 200 га худшей земли (25·200=5000 ц). Проведенный анализ позволяет построить оптимальный план для поставленной задачи (табл. 15).

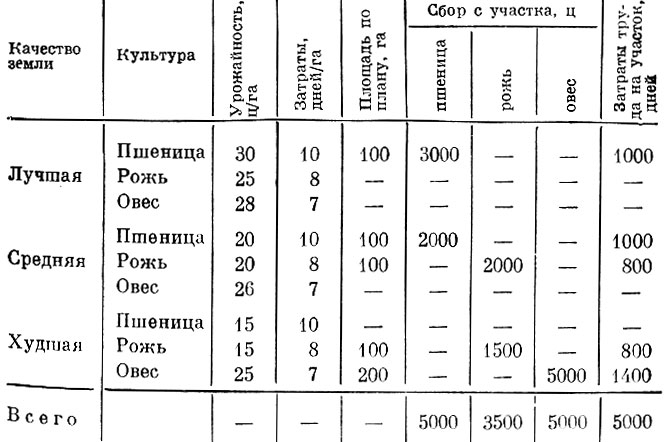
Таблица 15

Читателю, разобравшемуся в материале предыдущих параграфов, ясно, что в этой задаче о. о. оценки получат все культуры, а также более эффективные природные ресурсы - лучшая земля и земля среднего качества. Худшая земля будет иметь нулевую оценку, так как она имеется в избытке. Каковы же эти о. о. оценки? Двигаясь по табл. 15 снизу вверх, найдем такие оценки (выраженные в труде) для центнера каждой культуры и для использования гектара земли лучшего и среднего качества.

Производство 25 ц овса требует 7 дней труда: в оценке овса не участвуют затраты, связанные с использованием лучших земель, так как овес засевается только на земле худшего качества. Поэтому о. о. оценка овса будет равна 7:25=0,28 дня/ц.

Оценка центнера ржи на худшей земле составит 8:15=0,533 дня. С гектара земли среднего качества получают 20 ц ржи, которые, если бы они производились на худшей земле, требуют 20·0,533=10,67 дня, в то время как на земле среднего качества эти затраты составляют 8 дней. Так как 10,67-8=2,67 дня, эта цифра и принимается в качестве оценки использования гектара земли среднего качества.

Поскольку с гектара такой земли снимается 20 ц пшеницы, к видимым затратам в 10 дней следует прибавить оценку использования этого гектара (2,67 дня). Полученный результат (12,67 дня/га) представляет полные затраты на производство 20 ц пшеницы на земле среднего качества. Отсюда о. о. оценка центнера пшеницы равна 12,67:20=0,633 дня. По этой оценке 30 ц пшеницы, полученные с гектара лучшей земли, оцениваются в 30·0,633=19 дней. Видимые затраты составляют 10 дней, значит о. о. оценка использования гектара лучшей земли равна 19-10=9 дней.

С помощью найденных оценок по обычным правилам можно убедиться в том, что план, приведенный в табл. 15, действительно оптимален. Мы не будем приводить здесь расчетов, а ограничимся тем, что укажем окончательные данные о структуре затрат с учетом ренты (табл. 16).

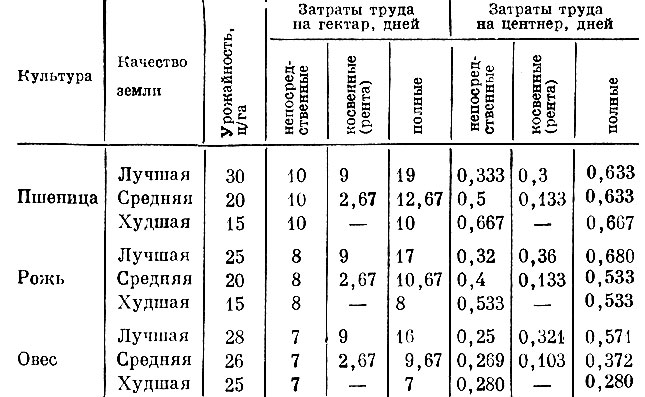
Таблица 16

Из этой таблицы видно, что в плане используются те способы" для которых суммарные затраты на производство центнера каждой культуры наименьшие (соответствующие данные выделены в таблице жирным шрифтом). Для использованных в плане способов суммарные затраты равны оценке продукции, для неиспользуемых они больше указанной оценки.

Пример, рассмотренный нами, еще одно доказательство преимуществ анализа на основе оптимальных решений. Если принимать во внимание только непосредственно затраты без ренты, как это нередко делается, то рожь может оказаться (в данном примере) оцененной выше пшеницы, хотя пшеница на любой земле требует больших затрат на производство, чем рожь. Точно так же, если ориентироваться на непосредственные, видимые затраты, следует признать, что посевы на худшей земле вообще нерентабельны, и т. д.