2. Задача о выборе производственной программы

Одним из важнейших вопросов, возникающих при конкретном экономическом анализе производства, является выбор и распределение производственной программы. Существует много способов решения этого вопроса: изготовление одного и того же изделия на различных предприятиях, изменение объемов плановых заданий выпуска данного изделия и др. Естественной поэтому является задача выбора такой производственной программы, при которой каждое предприятие использовалось бы для выпуска таких изделий, которые на нем целесообразнее всего изготавливать, в результате чего либо общий эффект достигает максимума, либо общие затраты становятся минимальными. Этот математический подход гораздо рациональнее часто встречающейся механической разверстки программы, он исключает волевые решения и позволяет осуществить научно обоснованное распределение производственной программы между предприятиями.

Задача о выборе производственной программы (заметим в скобках, что она была первой практической задачей линейного программирования, которую один из авторов настоящей работы решил в 1939 г.) описывается следующим образом. Имеется m предприятий, на которых нужно произвести n продуктов в заданном ассортименте l₁, l₂,..., l_n. Известна производительность i-го предприятия в единицу времени, если оно выпускает j-й продукт (a_ij). Предполагается, что max a_ij>0, т. е. каждый продукт может производиться хотя бы на одном предприятии. Требуется составить программу работы предприятий (указать долю времени, отведенную на производство каждого продукта на данном предприятии), причем так, чтобы получить максимальную суммарную продукцию в заданном ассортименте в единицу времени. Иначе говоря, имеется в виду случай, когда продукция дефицитна, производственные мощности ограничены и должны полностью использоваться.

Обозначим через x_ij(i=1, 2, ..., m; j=1, 2, ..., n) долю рабочего времени i-го предприятия, отводимую под j-й продукт. Поиск оптимальной программы загрузки предприятий сводится к решению следующей задачи: найти числа x_ij из условий

(1)

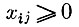
(доля времени не может быть отрицательной);

(2)

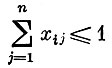
(сумма всех долей не превосходит полного времени работы предприятия);

(3)

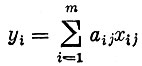
(количество j-го продукта, произведенное на всех предприятиях);

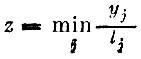
(количество ассортиментных наборов продуктов);

z - достигает максимума.

На основании общей теоремы линейного программирования (см. гл. I, § 4) оптимальный план характеризуется тем, что существуют оценки q₁, q₂, ..., q_n Для производимых продуктов (точнее, для работ по их изготовлению, т. е. чистой продукции) и d₁, d₂, ..., d_m для рабочего времени различных предприятий, которые дают

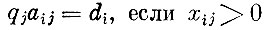
(если i-e предприятие выпускает j-й продукт, то оценка полученного в единицу времени продукта равна оценке единицы времени этого предприятия);

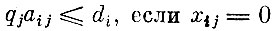
(если i-e предприятие не выпускает j-го продукта в оптимальном плане, то оценка продукта, который можно было бы получить в единицу времени на этом предприятии, не превосходит оценки единицы времени i-го предприятия);

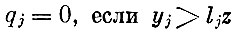
(если продукт избыточен, то его оценка равна нулю. Разумеется, избыточность продукта понимается только в рамках данной задачи. Избыточный продукт - это продукт, произведенный в объеме, превышающем ассортиментный, нереализуемый);

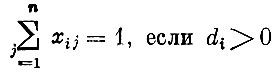
(если оценка единицы рабочего времени предприятия положительна, то предприятие занято все установленное время).

Все эти формулы характеризуют оптимальный план. В нем каждое предприятие используется для выпуска именно тех продуктов, которые наиболее целесообразно производить именно на этом предприятии. В соответствии с таким планом на каждом предприятии принят к производству тот вид продукции, для которого оценка чистой продукции предприятия оказывается наибольшей, а каждый вид продукции изготовляется на том предприятии, оценка расхода времени которого наименьшая. Иначе говоря: если x_ij>0, то

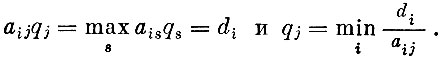
Можно охарактеризовать оптимальный план и с точки зрения затрат на его реализацию. Как правило, все затраты на выпуск продукции состоят из двух частей: из затрат, не зависящих от того, где выпускается данный продукт (материальные затраты), и затрат на работу предприятия, не зависящих от вида производимой на нем продукции. Раз это так, то даже без всяких формул ясно, что оптимальный план дает минимально возможные затраты на весь комплексный выпуск продукции. Ведь согласно оптимальному плану за данный период производится наибольшее число комплектов, и, значит, по любому другому плану для выполнения того же числа комплектов потребуется больший срок. А это приведет к тому, что часть затрат, связанных с работой предприятий, возрастет, материальные же затраты по крайней мере не уменьшатся.

Поскольку мы коснулись вопроса о затратах и показали, что для оптимального плана они минимальны, целесообразно подробнее рассмотреть структуру цен произведенных продуктов и ввести в связи с этим понятие прокатной оценки, чрезвычайно важное как при формировании цен, так и вообще в экономическом анализе.

Рассмотрим вполне реальную ситуацию. На двух предприятиях изготавливается (считаем для удобства - в одинаковых количествах) один и тот же продукт, но одно из них оснащено самой современной техникой, а на втором действует устаревшее оборудование. Цены, по которым продается продукт, одинаковы для обоих предприятий, затраты же на его производство на первом предприятии будут меньше, чем на втором. В результате первое предприятие окажется рентабельнее второго, его работников будут отличать и поощрять, хотя их заслуга в этом не так уже велика - лучшие результаты предопределены лучшими условиями.

Для избавления от такой, явно несправедливой и дезориентирующей оценки, целесообразно, чтобы предприятие, имеющее более совершенную технику, вносило государству определенный платеж за использование этой техники. Такие отчисления, уравнивающие доходы по-разному оснащенных предприятий, и носят название прокатных оценок, или ренты. В настоящее время они в некоторой степени находят выражение в плате за фонды, дифференцированных отчислениях от прибыли и других платежах.

Значение математического подхода состоит здесь в том, что он дает возможность объективного, научно обоснованного исчисления размера этих платежей на базе о. о. оценок.

Поясним принцип исчисления таких оценок и их взаимосвязь с ценами продукции. Естественно считать, что цена единицы продукта состоит из трех частей: затрат на материалы, затрат на работу предприятия, отнесенных к единице продукта, и чистого дохода предприятия, также отнесенного к единице продукта. Именно при такой структуре цены и правильно исчисленной норме дохода оказывается, что цена изделия одна и та же на всех предприятиях, на которых данное изделие целесообразно изготавливать.

Введем еще несколько обозначений. Пусть A_j - цена j-го продукта; C_j - материальные затраты в рублях на выпуск единицы j-го продукта; V_i - расход предприятия на функционирование в течение единицы времени; P_i - чистый доход предприятия. Тогда, если цены назначены исходя из соотношения

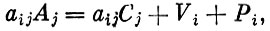
то на i-м предприятии затраты на производство j-го продукта окупаются. Если же в этой формуле вместо знака = стоял бы знак >, то выпуск j-го продукта на i-м предприятии был бы сверхрентабельным, а если знак <, то нерентабельным.

Опираясь на изложенный анализ задачи, нетрудно показать, что на основе оптимального плана и его оценок формируются именно такие взаимно согласованные нормы дохода и цены, при которых для всех реально производимых видов продукции выполняется указанное выше соотношение и никакие более рентабельные возможности не упущены. Иначе говоря, оптимальный план полностью согласуется с хозрасчетом (более подробно этот вопрос исследуется в последней главе).

В заключение параграфа приведем простой числовой пример. Имеются три предприятия, деятельность которых характеризуется следующими производственно-экономическими данными (табл. 11).

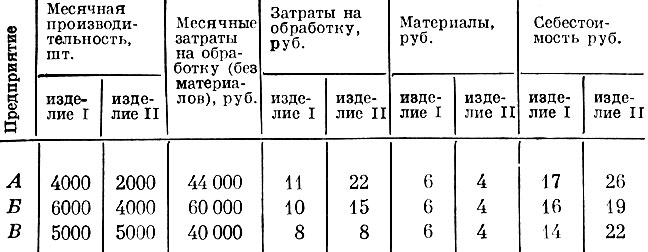
Таблица 11

В табл. 11 указана месячная производительность каждого предприятия, если оно будет выпускать либо первое, либо второе изделия, и, кроме того, выделены затраты на работу каждого предприятия, которые не зависят от вида изделий. Нужно, чтобы за год было произведено одинаковое число изделий I и изделий II. Оптимальный план загрузки предприятий должен указать, сколько месяцев в году каждое предприятие производит первое изделие и сколько второе, чтобы общий выпуск изделий был максимальным.

Это задача та же, что в общем виде была рассмотрена в этом параграфе, но в данном случае, когда идет речь всего о двух изделиях, совсем легко сообразить, как составить оптимальный план. Из табл. 11 следует, что на предприятии А вместо одного изделия II можно изготовить два изделия I, а на предприятиях Б и В соответственно полтора и одно изделие I. Значит, первое изделие целесообразнее всего производить на предприятии А, второе изделие - на предприятии В, а время работы предприятия В разделить между этими изделиями. Ясно также, что оценки для изготовления изделий в оптимальном плане относятся как 2:3. Этот оптимальный план дан в табл. 12, а приведенный в ней расчет чистой продукции по оценкам обосновывает его оптимальность.

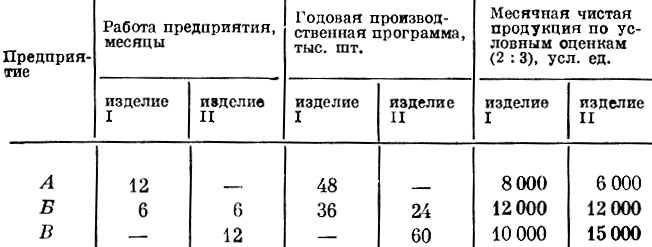
Таблица 12

В оптимальном плане на каждом предприятии производятся изделия, которые для него более выгодны. Соответствующие оптимальному плану оценки месячной продукции в таблице набраны жирным шрифтом. Предположим, что установленная оптовая цена комплекта из двух видов изделий равна 40 руб., а затраты материалов на одно изделие составляют соответственно 6 и 4 руб. Тогда цена обработки (изготовления) комплекта должна быть принята равной 40-6-4=30 руб. Поскольку оценки изготовления изделий I и II относятся как 2:3, то цены обработки каждого изделия должны равняться 12 и 18 руб. Теперь можно определить цену каждого изделия, так как она складывается из материальных затрат и цены обработки. Получаем A₁=6+12=18 руб., A₂=4+18=22 руб.

Цена изготовления каждого изделия определяется затратами по изготовлению и запланированным доходом с одного изделия. Исходя из этого легко рассчитать доход каждого предприятия от выпуска изделия I и изделия II (см. табл. 13).

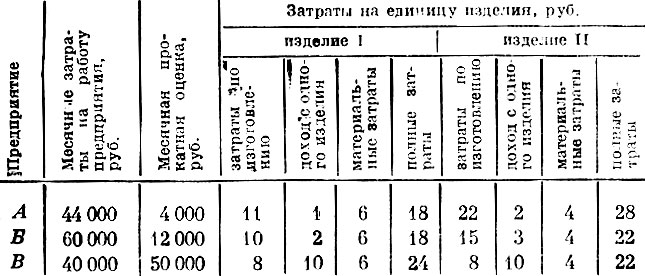
Таблица 13

Итак, чистый доход предприятий составляет P₁=4000 руб. (для предприятия А), P₂=12000 руб. (для предприятия Б) и P₃=50000 руб. (для третьего предприятия, В). Например, для предприятия А чистый доход P₁=4000·18-4000·6-4000·11=4000 руб. в месяц^*. На основе таких нормативов дохода, которые устанавливаются при рациональном использовании предприятий и рациональных ценах, целесообразно строить экономические показатели работы предприятий, дифференцированную плату за фонды, план прибыли и т. д. Решения, соответствующие оптимальному плану, оказываются выгодными и предприятиям и обществу, нерациональные же - отчетливо демонстрируют свою невыгодность. Кроме того, оценки оптимального плана могут служить для принятия правильных оперативных решений при появлении новых возможностей, не предусмотренных планом. Например, обнаружена возможность дополнительного выпуска изделий II на предприятии В путем использования менее производительных станков - применения способа с затратами 12 руб. вместо 8 руб. на изготовление одного изделия. Следует ли реализовать такую возможность?

^* (Смысл этих величин (норм дохода) состоит в том, что они выражают тот вклад в общий доход, который может быть получен ©т данного предприятия за один месяц (если предприятие будет работать лишний месяц, мы получим эту сумму). Иначе говоря, если бы предприятие А можно было получить для использования дополнительно на один месяц ("взять напрокат"), то наш комплекс мог бы дать дополнительный доход в 4000 руб. Отсюда происходит упоминавшийся выше термин "прокатная оценка".)

Правильное решение состоит в том, чтобы организовать дополнительный выпуск изделий на данном предприятии: затраты (12+4=16 руб.) будут ниже 22 руб. - рассчитанной цены на их изготовление, следовательно, увеличение выпуска продукции повысит доход комплекса предприятий в целом. Такое решение и подсказывается оптимальным подходом. Если же подойти к этому вопросу так, как нередко делается на практике, исходя из показателя себестоимости, то было бы принято неверное решение.

Существуют и другие модели задачи о распределении производственной программы, учитывающие иные условия или дополнительные факторы и усложняющие обстоятельства. Например, если объем продукции задан и полной загрузки всего оборудования не требуется, то проблема состоит в распределении программы, при которой заданное количество продукции получалось бы с наименьшими затратами. Все эти и более сложные постановки задачи обычно решаются методами линейного (впрочем, иногда и нелинейного) программирования, в результате которых наряду с планом строится согласованная с ним система экономических показателей.

В качестве одного из многих примеров практического применения задачи о выборе производственной программы можно упомянуть проведенный Институтом математики СО АН СССР совместно с рядом металлургических институтов и Союзглавметаллом расчет рациональной загрузки прокатных станов СССР - размещения заказов на трубы, мелкий и средний сорт и другие виды продукции. Оказалось, что при имеющемся сейчас оборудовании только благодаря правильному распределению заказов можно получить по каждой из рассмотренных групп значительно больше проката, не увеличивая при этом объема перевозок. Несмотря на большие размеры задачи (тысячи ограничений и десятки миллионов способов), расчет выполняется за несколько десятков часов машинного времени.

заказать кредитную карту