1. Транспортная задача

В современной экономике большую роль играют проблемы, связанные с транспортировкой грузов. Они обусловлены удаленностью источников сырья от пунктов производства, пунктов производства от пунктов потребления и другими объективными факторами. Затраты на перевозки всех видов грузов всеми видами транспорта в целом по стране составляют более 20 млрд. руб. Столь большой объем затрат дает основание полагать, что при правильном решении вопросов, связанных с использованием транспорта, особенно учитывая, с одной стороны, разнообразие его видов, богатство природных условий, сложность схем перевозок, дальность расстояний, а с другой - дефицитность транспортных средств и их загруженность, можно ожидать существенного сокращения этих затрат. Такое предположение подтверждается и значительным уже опытом применения математических методов планирования на транспорте.

Остановимся на некоторых характерных особенностях транспортных задач. Прежде всего - проблема оптимальности. Что значит транспорт работает хорошо? Один из основных показателей работы транспорта - грузооборот - измеряется в тонно-километрах. Получается, если транспортная организация "выполнила" много тонно-километров, то она работала хорошо. А ведь оптимальная система перевозок, несомненно, приносящая пользу государству, ведет к сокращению этого показателя и тем самым ухудшает показатели работы организации. Можно, конечно, измерять качество работы по затратам при существующих тарифах и пытаться, планируя перевозки, минимизировать эти затраты. Но тогда сразу же возникает вопрос о правильном, научно обоснованном исчислении тарифов.

Очень эффективно, например, было бы оптимально планировать совместную деятельность сразу нескольких видов транспорта. Но возникающая при этом математическая задача будет иметь весьма большой размер, что, естественно, затруднит поиск оптимального решения, и без того осложненного тем, что такая задача "принадлежит разным ведомствам". В общем здесь есть еще немало вопросов, ждущих своего решения с помощью точных математических методов.

К задаче транспортировки грузов тесно примыкают и задачи оптимальной маршрутизации. Краткая характеристика их такова. Пусть речь идет о перевозке различных грузов между несколькими пунктами погрузки и разгрузки, причем адреса перевозок указаны заранее. Тогда дело сводится к определению того, куда нужно перебрасывать высвободившиеся вагоны или автомашины, чтобы суммарные затраты на перевозки были минимальны, т. е. чтобы минимизировалось количество "холостых" рейсов (о решении этих проблем на основе модели транспортной задачи см. ниже).

Обсудив некоторые общие свойства транспортных проблем, построим математическую модель, описывающую одну довольно простую, но типичную ситуацию. Речь будет идти о рациональной перевозке некоторого однородного (одного и того же назначения и качества) продукта от производителей к потребителям. В этом случае каждому потребителю безразлично, откуда, из каких пунктов производства будет поступать этот продукт, лишь бы он поступал в нужном объеме. Однако от того, насколько рациональным окажется прикрепление пунктов потребления к пунктам производства, существенно зависит объем транспортной работы. В связи с этим, естественно, возникает вопрос о наиболее рациональном прикреплении производителей к потребителям (и наоборот), о правильном направлении перевозок груза, при котором потребности удовлетворяются, а затраты на транспортировку минимальны.

Пусть имеются пункты производства А₁, А₂, ..., А_n с объемами производства в единицу времени (месяц, квартал), равными соответственно a₁, a₂, ..., a_n, и пункты потребления B₁, B₂, ..., B_m с объемами потребления, равными b₁, b₂, ..., b_m соответственно. Будем предполагать, что производство и потребление сбалансированы - сумма объемов производства равна сумме объемов потребления, т. е.

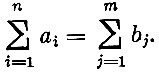
Предполагаются известными величины C_ij - затраты по перевозке единицы продукта из i-го пункта производства в j-й пункт потребления. Они могут быть выражены в стоимостной (денежной) форме или в натуре (например, в тонно-километрах). Требуется найти такой план перевозок, при котором были бы удовлетворены потребности в пунктах B₁, B₂, ..., B_m и при этом суммарные затраты на перевозку были бы минимальны.

Обозначая через x_ij количество продукта, перевозимое из i-го пункта производства в j-й пункт потребления, приходим к следующей математической формулировке задачи.

Найти минимум

(*)

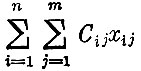
(суммарные затраты на транспортировку) при условиях

(1)

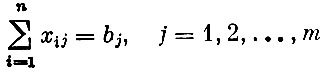
(в каждый пункт потребления завозится требуемое количество продукта);

(2)

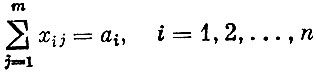
(из каждого пункта производства полностью вывозится произведенный продукт);

(3)

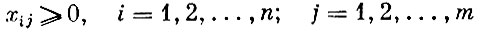
(перевозимый объем продукта не может быть отрицательным).

Всякий набор величин x_ij(i=1, ..., n; j=1, ..., m), удовлетворяющих условиям (1)-(3), будем называть допустимым планом перевозок. План, для которого суммарные затраты достигают минимума, называется оптимальным.

Поскольку транспортная задача является частным случаем задачи линейного программирования, для нее справедлив приведенный ранее критерий оптимальности плана. Используя терминологию и особенности транспортной задачи, этот критерий можно сформулировать таким образом: допустимый план перевозок тогда и только тогда является оптимальным, когда каждому пункту производства и потребления можно сопоставить величину, характеризующую уровень оценки продукции в нем так, что множество этих потенциалов удовлетворяет следующим условиям: (1) разность оценок пунктов потребления и производства, между которыми запланированы перевозки, равна затратам по транспортировке единицы продукта между этими пунктами; (2) аналогичные разности для всех остальных пар пунктов не превосходят затрат по транспортировке.

Если ввести обозначения: U_i - потенциал для i-го пункта производства и V_j - потенциал для j-го пункта потребления, то эти условия можно представить как

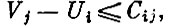
причем V_j-U_i=C_ij, если перевозка из пункта A_i в пункт B_j предусмотрена в плане (x_ij>0).

В транспортной задаче оценки или, как их чаще называют в этом случае, потенциалы имеют особенно прозрачный экономический смысл. Они выступают здесь как локальные (поясные) цены (или наценки к единой цене), создающие заинтересованность в правильном направлении перевозок. При такой интерпретации признак оптимальности плана представляет собой по сути математическое выражение здравого смысла - если какая-то перевозка осуществляется, то цена в пункте потребления равна цене в пункте производства плюс транспортные затраты; в остальных случаях цена V_j не может быть больше, чем U_i+C_ij, так как продукт в пункте B_j по такой цене можно было бы получить, привезя его с затратами C_ij из пункта A_i. Следовательно, V_j≤U_i+C_ij, т. е. в обоих указанных случаях разность цен не превышает затрат по перевозке. С помощью критерия оптимальности, так же как и в задаче о раскрое, можно не только проверить на оптимальность любой план, но и в случае его неоптимальности указать способ улучшения этого плана.

Рассмотрим теперь процесс формирования оптимального плана транспортной задачи. Возьмем конкретный числовой пример и, применив метод последовательного улучшения, детально покажем, как строится такой план.

Пусть заданы объемы производства a₁=95, a₂=55, a₃=50 и объемы потребления b₁=48, b₂=54, b₃=31, b₄=37 и b₅=30. Затраты на перевозки записаны в табл. 6 в виде матрицы. Например, число 90 означает, что перевозка единицы продукта из пункта A₁ в пункт B₁ обходится в 90 единиц (скажем, эти числа могут означать расстояния между пунктами; если объем дан в тоннах, затраты выражаются в тонно-километрах).

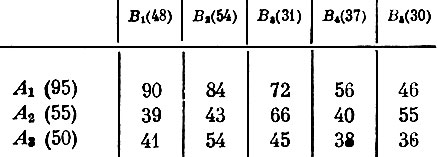
Таблица 6

Решение задачи начнем с построения некоторого допустимого плана. Вообще говоря, это можно сделать разными способами, и мы воспользуемся одним из них. В матрице затрат отыскиваем минимальный элемент (в данном примере 36) и включаем в план в максимально возможном объеме самую дешевую перевозку, притом в максимально возможном объеме (в нашем примере это перевозка 30 единиц из пункта A₃ в пункт B₅). Следующий по величине элемент матрицы затрат (38) определяет включение в план перевозки между пунктами A₃ и B₄. Объем перевозки равен только 20 единицам, так как этим количеством груза исчерпываются возможности предприятия, расположенного в пункте A₃. Продолжая действовать аналогично и дальше, придем к плану перевозок, показанному в табл. 7. Этот план допустим: суммы строк соответствуют объемам производства, а столбцов - объемам потребления. Затраты на его реализацию составляют: 54·84+31·72+10·56+48·39+7·40+20·38+30·36=11320.

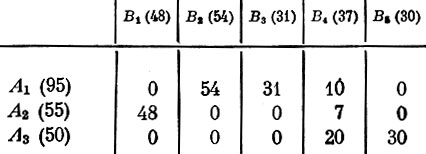
Таблица 7

Для того чтобы проверить полученный план на оптимальность, прежде всего вычисляем систему потенциалов (оценок единицы продукта) в пунктах производства (U₁, U₂, U₃) и пунктах потребления (V₁, V₂, V₃, V₄, V₅). Так как потенциалы определяются с точностью до постоянного слагаемого, какой-нибудь из них можем задать заранее. Пусть, например, U₁=100 и связи производителей с потребителями в плане осуществляются по направлениям, которые указаны на рис. 5. Тогда, зная, что разности потенциалов между пунктами потребления и пунктами производства, связанными в плане, равны соответствующим транспортным затратам, один за другим находим остальные потенциалы:

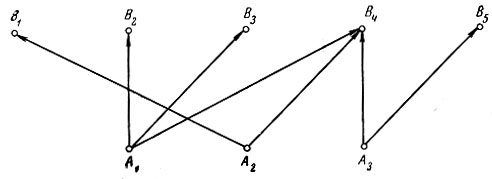
Рис. 5

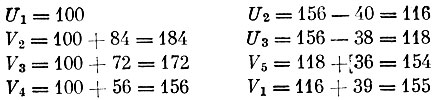
Проверим выполнение признака оптимальности. Для этого, согласно условию (2), нужно подсчитать величины V_j-U_i-C_ij. Если они все меньше или равны нулю, то план оптимален. Несоблюдение этого требования означает, что план может быть улучшен. Находим

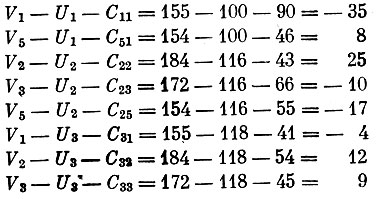
Для пунктов, между которыми предусмотрены перевозки, эти разности, очевидно, отвечают признаку оптимальности. Но так как некоторые из полученных величин положительны, весь план не оптимален. Чтобы его улучшить, введем в план перевозку в объеме θ между какими-нибудь пунктами A_i и B_j, для которых соответствующая разность положительна. Логичнее всего ввести эту перевозку между пунктами A₂ и B₂, так как для них величина разности наиболее значительна (25). Введение добавочной перевозки нарушает сбалансированность плана, т. е. объем ввоза (вывоза) в пункт не соответствует потреблению (производству) в нем. Поэтому необходимо одновременно изменить объемы перевозок и между некоторыми другими пунктами. Эти изменения следует произвести по направлениям B₂A₁, A₁B₄ и B₄A₂, т. е. согласно тем связям, по которым производилось определение потенциалов (см. рис. 5). В табл. 8 приведен план, в котором осуществлены все необходимые изменения в объемах перевозок.

Таблица 8

Нетрудно проверить, что этот план сбалансирован - из каждого пункта вывозится столько, сколько в нем производится, а каждый пункт потребления удовлетворяет всю свою потребность. Легко убедиться, что затраты по реализации этого плана перевозок меньше первоначальных на величину (V₂-U₂-С₂₂)θ=259. Следовательно, выгодно выбрать θ как можно большим. Учитывая, что объемы перевозок не могут быть отрицательными, наибольшее из возможных значений θ равно 7. Полагая θ=7, находим новый допустимый экономически более выгодный план. Он приведен в табл. 9.

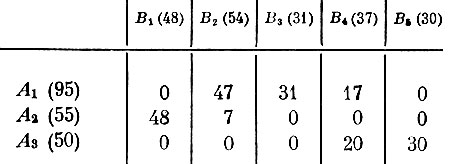
Таблица 9

Нахождением нового допустимого плана заканчивается, как говорят математики, первое приближение (первая итерация). Дальше аналогичные операции проводятся снова, но уже для нового плана. Прежде всего вычисляются потенциалы, проверяются условия оптимальности. Если они выполнены, то решение закончено. Если нет, то снова производится переход к лучшему плану и т. д.

Для окончательного решения задачи требуется выполнить еще три итерации. Чтобы не увеличивать объема книги, эти итерации здесь не приводятся. Если же читатель заинтересуется дальнейшим ходом решения, он может сам проделать все необходимые расчеты и сравнить свой результат с оптимальным планом, приведенным в табл. 10.

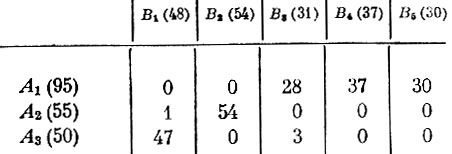
Таблица 10

Чтобы убедиться в оптимальности этого плана, нужно снова вычислить потенциалы пунктов производства и пунктов потребления, а затем удостовериться, что величины V_j-U_i-C_ij≤0. Приведем эти вычисления:

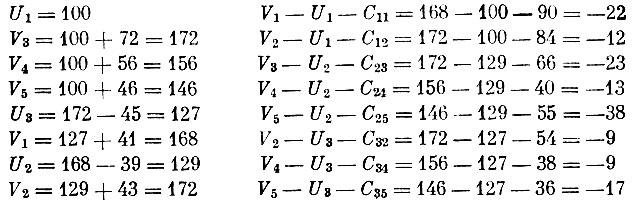
Все же остальные значения V_j-U_i-C_ij равны нулю. Следовательно, в силу критерия оптимальности найденный план - наилучший, оптимальный. Затраты на его реализацию составляют 28·72+37·56+30·46+39·1+43·54+47·41+45·3=9891.

По сравнению с первым допустимым планом, который представлялся на первый взгляд также весьма разумным, затраты в оптимальном плане уменьшились примерно на 13%.

Мы рассмотрели транспортную задачу в матричной, или "шахматной" постановке. Такое название этой постановки связано с тем, что информация о расстояниях и грузопотоках задана в виде "шахматной" таблицы-матрицы. Нередко, однако, приходится сталкиваться и с другой формой транспортной задачи - транспортной задачей в сетевой постановке. Если при матричной постановке задачи предполагаются известными затраты по транспортировке единицы продукта из каждого j-го пункта производства в i-й пункт потребления, то при сетевой постановке указываются затраты по перевозке на отдельных участках сети, а полные затраты получаются в результате суммирования. Поэтому при использовании различных путей, соединяющих пункты, затраты различны. Здесь в ходе решения определяются не только объемы, но и маршруты перевозок. Доказано, что обе постановки транспортной задачи эквивалентны, т. е. можно перейти от одной к другой и решение при этом не изменится. Тем не менее необходимости в таком переходе нет, так как метод потенциалов применим и к задаче в сетевой постановке.

Рассмотрим, например, транспортную задачу в конкретных условиях, приведенных на рис. 6. Пункты производства на нем обозначены прямоугольниками, пункты потребления - кружками, а промежуточные пункты - треугольниками. Числа в скобках со знаком плюс указывают объемы производства, со знаком минус - объемы потребления, а числа, стоящие возле участков пути, выражают транспортные затраты по перевозке единицы продукта между соответствующими пунктами. В результате решения, ход которого мы не будем приводить здесь, можно найти рациональные грузопотоки, а также систему потенциалов, выражающих цену единицы продукта в различных пунктах, включая обусловленную планом рациональную транспортную наценку. На рис. 6 числа, стоящие у вертикальных отрезков, равны потенциалам, а стрелки на контуре указывают направление рациональных перевозок.

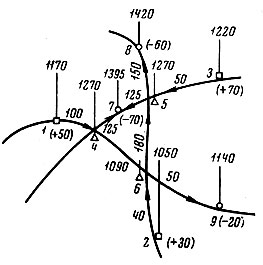
Рис. 6

Еще раз отметим замечательную согласованность между оптимальным планом и ценами, установленными в соответствии с потенциалами. Для рациональных направлений перевозок (указанных в плане стрелками) разность цен в точности совпадает с затратами на перевозку, т. е. эти перевозки оправданы и выгодны как для производителей, так и для потребителей (например, для пунктов 2 и 6 затраты по перевозке равны 1090-1050=40). Те же перевозки, которые нерациональны в данных условиях и не рекомендованы в плане, оказываются невыгодными - прирост в цене меньше транспортных затрат (например, перевозка из пункта 1 в пункт 8 явно невыгодна, так как транспортные затраты равны 500, а разность цен меньше этой величины: 1420-1170=250).

Математическая модель транспортной задачи получает все большее и большее практическое применение. В настоящее время в Государственном комитете по материально-техническому снабжению на основе методики, разработанной по этой модели, произведено прикрепление и составлены рациональные планы перевозок для десятков видов продукции химической промышленности, промышленности строительных материалов и продукции других отраслей хозяйства, что дает миллионы рублей экономии в затратах на железнодорожный транспорт.

Упоминавшаяся в начале этого параграфа задача маршрутизации может быть также решена с помощью транспортной модели. Для этого нужно принять в качестве однородного груза ... пустые вагоны, направляемые от пункта выгрузки к пунктам погрузки. Полученное распределение, которое без труда находится на основе транспортной задачи, дает решение задачи об оптимальной маршрутизации, так как оно определяет пути следования вагонов.

Практическое применение транспортной задачи для решения задач оптимальной маршрутизации получило особенное распространение на автотранспорте. В ряде крупных городов производится ежедневный расчет рациональных маршрутов на ЭВМ и на их основе заполняются наряды для значительного процента автомашин. В некоторых небольших автохозяйствах эту методику хорошо освоили и регулярно используют сами диспетчеры. Это позволяет в ряде случаев снижать холостой пробег на 30-50%. Об эффекте применения оптимальной маршрутизации свидетельствует и такой любопытный факт. В одном автохозяйстве, где проводился эксперимент по введению наилучшей маршрутизации транспорта, шоферы, ездившие по оптимальным маршрутам, найденным с помощью метода потенциалов, имели на своих машинах отличительные флажки. Через несколько дней после начала эксперимента шоферы наглухо припаяли флажки к машинам, так как они стремились и впредь получать "математические" наряды. Большая эффективность работы этих машин была выгодна не только для автохозяйства в целом, но и для каждого из водителей.

Необходимо подчеркнуть, что постановка транспортной задачи в наибольшей степени характерна именно для социалистической экономики. Критерием оптимальности в этой задаче является минимум суммарных затрат по перевозке груза, т. е. народнохозяйственный эффект, а не выгода отдельных грузополучателей. Ясно, что не только цель, но и сама возможность широкой реализации решения, требующая переформирования всех грузопотоков в масштабах страны, осуществима лишь в условиях научно планируемой экономики. Причем решение транспортной задачи обеспечивает условия для установления экономически обоснованной, дифференцированной системы цен (или транспортных накидок), делающей рациональные прикрепления экономически выгодными и взаимоувязанными для всех производителей и потребителей данной продукции. Такие цены способствуют реализации оптимальных решений в хозяйственной деятельности.

Очень важно знать, что транспортная задача используется не только для решения транспортных проблем. Ее первое применение действительно осуществлялось на примере этой отрасли народного хозяйства, но вообще математическая модель транспортной задачи может описывать самые разные ситуации, очень далекие от перевозок. Задача, о которой сейчас пойдет речь, - задача размещения производства - лишний раз подтверждает это положение.

Пусть в пунктах A₁, A₂, ..., A_m имеются или могут быть размещены предприятия, производящие некоторый продукт. В пунктах B₁, B₂, ..., B_n потребности в этом продукте заданы и равны соответственно b₁, b₂, ..., b_n. Затраты по производству единицы продукта в пункте A_i равны C_i, возможный объем производства a_i, а затраты по транспортировке единицы продукта из A_i в B_j равны C_ij. Задача состоит в выборе мест расположения новых предприятий, объема производства и плана перевозок так, чтобы суммарные затраты по производству и транспортировке всего потребного объема продукта были минимальны.

Первое осложнение при такой постановке задачи заключается в том, что возможный суммарный объем производства, как правило, не сбалансирован и превышает суммарный объем потребления (это так называемая открытая транспортная задача, рассмотренная же ранее называется закрытой). Преодолеть такое затруднение можно, введя добавочный фиктивный пункт потребления B_n+1 со следующими характеристиками: потребность продукта в нем равна разности между возможным объемом производства продукта и суммарной потребностью всех реальных пунктов потребления (это значит, что в такой пункт свозятся все излишки), а затраты на перевозку в него из всех пунктов производства равны нулю. В результате приходим к обычной транспортной задаче, в которой, однако, в элементах матрицы затрат к затратам на транспортировку добавлены затраты на производство в пункте отправления. Решив эту задачу, определим, в частности, оптимальные объемы производства как суммы потоков из каждого пункта производства в реальные пункты потребления.

Модель, которую мы рассматриваем, а также некоторые ее обобщения (вариантная постановка и др.) используются на практике и для текущего планирования производства, и для размещения предприятий при развитии отрасли в перспективе. В последнем случае в затратах учитываются также и необходимые капиталовложения (затраты на строительство или реконструкцию имеющихся предприятий). Рассчитанный на основе такой модели оптимальный план развития отрасли, в котором одновременно и совместно решается вопрос о размещении всех ее предприятий, оказывается значительно более эффективным, чем план, полученный в результате изолированного экономического анализа по отдельным предприятиям.

Несколько слов следует сказать о выборе целевой функции и вообще о постановке задачи размещения. Здесь используются две постановки. В первом случае требуется при ограниченных ресурсах произвести максимум продукции или, если известен ассортиментный состав продукции, то максимизировать количество ассортиментных наборов. В соответствии со второй постановкой требуется произвести заданный объем продукции с минимальными затратами. Обычно при решении задачи выбирается какая-то одна постановка и один тип целевой функции, но в ряде случаев бывает целесообразно использовать целевые функции обоих типов.

На основе модели транспортной задачи произведено большое число расчетов плана развития отраслей как по стране в целом, так и по отдельным крупным экономическим районам (Сибири, Казахстану и др.). В частности, такие расчеты по размещению и развитию отраслей проведены по производству цемента, ряда других строительных материалов, многим химическим производствам и т. д. Большое значение имеет ряд расчетов по топливно-энергетическому балансу, т. е. по определению рациональной структуры потребления и производства разных видов топлива, а также районов их распределения. Здесь специального упоминания заслуживает работа по исчислению замыкающих затрат на электроэнергию и топливо, которая была проведена в Энергетическом институте СО АН СССР.

Как правило, все эти расчеты базировались на транспортной модели, однако учет ряда дополнительных обстоятельств (например, различия эффективности разных видов топлива при том или ином использовании, наличие уже начатых работ по строительству предприятий и др.) заставлял вносить в эти расчеты различные коррективы и усложнения. Немалые осложнения возникали и при подборе технико-экономической информации, необходимой для практической реализации модели.

Несмотря на указанные трудности, расчеты на основе транспортной модели получают все более широкое распространение, так как они открывают перспективу получения значительного экономического эффекта. Как показывает опыт, в частности, полученный в Сибирском отделении АН СССР и в ЦЭМИ, с помощью таких расчетов обычно обнаруживаются возможности снижения объема капиталовложений не менее чем на 10-20%.