4. Общие модели производственного планирования

Задачи поиска оптимального решения в частных экономических моделях, как мог убедиться читатель, охватываются общей схемой линейного программирования. На основе такой схемы может быть произведен анализ задачи, даны эффективные средства нахождения оптимального решения и помимо оптимального плана найдены о. о. оценки различных ингредиентов (производственных факторов, продукции), которые служат базой эффективного экономического анализа и совершенствования плана. Опишем некоторые общие схемы применения оптимального математического программирования в планово-экономическом анализе.

Но сначала несколько предварительных замечаний. Нужно иметь в виду, что задачи текущего и перспективного планирования обладают существенными различиями. В первом случае речь идет о составлении плана на сравнительно краткий промежуток времени при определенных, более или менее неизменных условиях - используемых производственных процессах, ресурсах средств производства, требованиях к продукции. В перспективном планировании речь идет о составлении плана на сравнительно длительный период времени при существенных изменениях как в условиях, так и ресурсах. Иначе говоря, имеется в виду схема расширенного воспроизводства, при которой благодаря появлению новых производственных фондов меняется сама производственная база и выносятся долговременные решения о создании и использовании этих фондов, учитывается технический прогресс. Поэтому для задач того и другого типа необходимы различные модели.

Далее, в текущем планировании значительно разнятся задачи составления плана всего народного хозяйства, т. е. замкнутой экономической системы, располагающей собственными производственными ресурсами, определяющей и удовлетворяющей потребности общества (личные и общественные), и плана некоторого отдельного хозяйственного подразделения (предприятия, фирмы, комбината, отрасли, экономического района). Экономика такой системы является уже незамкнутой, ее функционирование рассчитано на получение ряда ингредиентов (сырья, материалов) извне и выдачу большой части продукции также внешним потребителям.

Наконец, при наличии иерархически упорядоченного комплекса хозяйств возникает проблема взаимосогласованного плана их действий для достижения оптимальных результатов всего комплекса.

Приведем математическое описание одной из упомянутых моделей, а также кратко обсудим некоторые особенности других задач.

Задача текущего производственного планирования (статическая модель). Эта задача состоит в том, чтобы исходя из определенных ресурсов (оборудование, рабочая сила, сырье), которыми располагает некое хозяйственное подразделение, например предприятие, с учетом реальных условий и ограничений (размеры поставок сырья и материалов, объем трудовых ресурсов или фонда зарплаты, величина заказов и требований на продукцию и т. п.) определить производственную программу и организовать ее выполнение так, чтобы достичь наилучших результатов. При построении математико-экономической модели такой задачи ряд вопросов, относящихся к ее структуре и исходной информации, должен быть детализирован и уточнен - прежде всего основные ингредиенты (виды материалов, продукции, оборудования, рабочей силы), принятая степень их объединения (агрегирования), имеющиеся ресурсы и ограничения, технологические и организационно возможные производственные способы, затрачиваемые и получаемые в них ингредиенты - все, что определяет матрицу задачи.

При этом среди затрачиваемых ингредиентов можно выделить расходуемые, которые полностью потребляются в течение одного производственного цикла (сырье, полуфабрикаты), и задалживаемые, остающиеся после использования практически в неизменном виде (станки, машины). Получаемые ингредиенты - это конечная продукция, задание по одним видам которой может быть точно зафиксировано, по другим - задано в определенных пределах, по третьим - связано с требованием комплектности, по четвертым - может целиком определяться самим предприятием. Различный вид могут иметь ограничения на сырье и материалы - жесткие лимиты и лимиты, зависящие от объема выпуска продукции. Очень существенно разделение ингредиентов на специфические для данного предприятия (установленное оборудование, полуфабрикаты) и на ингредиенты, участвующие во внешних связях (материалы, конечная продукция, привлекаемая рабочая сила).

Наконец, очень важным и часто не бесспорным является принятие критерия оптимальности. Для сопоставления результатов, получаемых в различных планах (вариантах решения), основное значение имеют переменные ингредиенты, т. е. те, по которым в разных вариантах получаются различные результаты (наибольшее значение имеют при этом внешние ингредиенты). В критерии оптимальности желательно для расходуемых ингредиентов добиваться минимума, а для производимых максимума. Однако, чтобы иметь возможность единого сравнения, они должны быть объединены в один критериальный показатель (целевую функцию). Типичными являются для такой функции требования максимума продукции (наборов) при данных затратах, минимума затрат на данную продукцию (или одного вида затрат - труда), максимума прибыли. В последнем случае обязательно, а в предыдущих - во многих случаях также необходимо, чтобы отдельные ингредиенты могли взвешиваться по некоторым оценкам или баллам. Хотя удовлетворительное согласование нескольких требований в одном критерии - достаточно сложное дело, оно все же нередко осуществимо. Доказательство тому - задача о выборе производственной программы, рассмотренная в § 2 настоящей главы, где одно и то же решение дает и максимум продукции, и минимум затрат, и максимальный доход. Определенные затруднения вызывает учет в критерии внешних условий: не всегда ясно, какие ресурсы могут быть предоставлены хозяйственному объекту и какие требования к нему предъявляются.

Приведенная схема описания задачи текущего планирования в одних случаях непосредственно делает ясной возможность ее записи в форме основной задачи линейного программирования, а в других случаях простыми приемами она сводится к этой задаче. Поэтому линейно-программные методы решения задачи позволяют производить расчет оптимального плана, а ее анализ дает о. о. оценки всех участвующих в производстве ингредиентов. Эти оценки очень полезны при анализе и оперативном корректировании плана. Они показывают, какой вклад дает каждая единица продукции, полуфабриката, сырья, трудовых ресурсов, часа работы того или иного оборудования в критерий оптимальности, какова оценка каждого ограничения. В результате удается не только выявлять, но и количественно оценивать узкие места производства, определять, за счет каких источников можно добиться наибольшего эффекта, и т. д.

Рассмотрев, какие именно факторы следует учитывать при моделировании задач текущего планирования, приведем в качестве иллюстрации математическую модель одной из возможных постановок такой задачи.

Пусть предприятие должно выпускать n видов продукции в заданной пропорции k₁:k₂: ...: k_n. Это предприятие располагает N - n видами производственных факторов (сырьем, трудовыми ресурсами, производственными мощностями и т. п.), имеющимися в объемах, равных соответственно b_n+1, b_n+2, ... ,b_N и r допустимыми технологическими способами. Каждый из этих способов определяется вектором

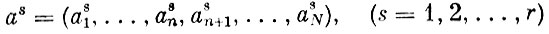
первые n компонент которого характеризуют выпуск продукции, а последние N - n - размеры затрат, соответствующие данному технологическому способу при однократном его использовании.

Выбрать текущий производственный план - это значит (на математическом языке!) указать вектор π=(x₁, ..., x_r) с неотрицательными компонентами, определяющими интенсивность применения каждого из возможных технологических способов. Понятно, что, выбрав план π, мы обеспечим выпуск i-то вида продукции в количестве

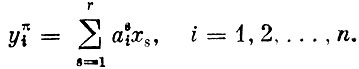
В качестве целевой функции - критерия качества планирования - выберем число ассортиментных наборов продукции, предполагая, что в один набор различные виды продукции входят в количествах, равных соответственно k₁, k₂, ..., k_n. Естественно будет искать такой план, который, удовлетворяя всем ограничениям, максимизирует целевую функцию.

Теперь уже можно записать экстремальную задачу, соответствующую задаче текущего производственного планирования.

Требуется найти вектор π=(x₁, ..., x₂) из условий

(1)

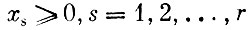
(интенсивности применяемых способов неотрицательны);

(2)

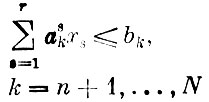
(ресурсы факторов не перерасходованы);

(3) величина

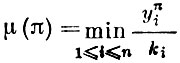
выражающая число ассортиментных наборов продукции, должна быть максимизирована.

Как обычно, план π, удовлетворяющий условиям (1) и (2), будем называть допустимым, а план, удовлетворяющий условиям (1)-(3) - оптимальным. На первый взгляд из-за формы условия (3) может показаться, будто получившаяся задача не является задачей линейного программирования. Однако это впечатление обманчиво. Обозначим μ(π) через y и перепишем задачу так.

Найти

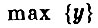
условий

(1′)

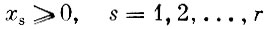
(2′)

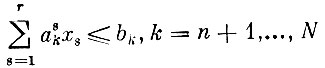
(3′)

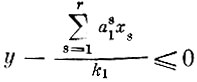
(количество ассортиментных наборов продукции определяется самым дефицитным ее видом).

Это теперь уже бесспорно задача линейного программирования. Для того чтобы дать характеристику оптимального плана получившейся задачи, введем о. о. оценки для всех рассматриваемых ингредиентов: c₁, c₂, ..., c_n - оценки продукции; c_n+1, c_n+2, ..., c_N - оценки производственных факторов.

Допустимый план π=(x₁, x₂, ..., x_r) будет оптимальным тогда и только тогда, когда найдены такие числа c₁, c₂, ..., c_n, c_n+1, ..., c_N, которые удовлетворяют следующим условиям:

а)

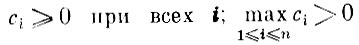
(оценки неотрицательны, причем хотя бы один из видов продукции имеет положительную оценку);

б)

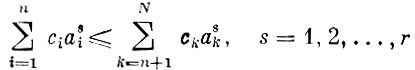
(при каждом технологическом способе оценка получаемой продукции не превосходит суммарной оценки затрачиваемых факторов - сырья, производственных мощностей, труда);

в)

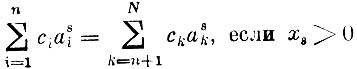
(для используемых способов оценка производимой продукции в точности равна суммарной оценке затрачиваемых факторов, т. е. соблюден принцип рентабельности);

г)

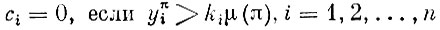
(если какой-либо вид продукции производится в избытке, то его оценка равна нулю);

д)

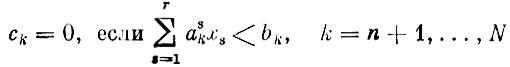
(если производственный фактор не используется полностью, то его оценка равна нулю).

Методы нахождения таких объективно обусловленных оценок были показаны выше. Отметим лишь, что их введение в расчеты повышает качество планирования. Например, использование прокатных оценок способствует более правильному использованию производственного оборудования. Сейчас еще нередко случается, что прогрессивная техника в одном месте простаивает, хотя в другом месте в ней очень нуждаются. Это во многом результат того, что задалживание дефицитного оборудования пока еще не оценивается количественно. Недостатки подобного рода можно было бы исправить, учитывая при управлении экономикой прокатные оценки, ренту за оборудование и за трудовые ресурсы.

Производственный план комплекса. Социалистическое общественное производство составляет единую систему с едиными целями и задачами и в то же время организационно и структурно представляет собой комплекс ряда отдельных хозяйственных единиц - предприятий и объединений, имеет сложную структуру и иерархию. Поэтому, когда речь идет о плане для народного хозяйства в целом или для некоторого хозяйственного объединения, то, собственно, нужно иметь не один план, а комплекс взаимоувязанных планов.

Для определенности будем рассматривать только две ступени - ряд предприятий и объединяющий их комплекс, замкнутый и автономный. Этот комплекс имеет ресурсы как жестко закрепленные за отдельными предприятиями, так и по некоторым ингредиентам (в целом или в определенной части) находящиеся в распоряжении всего комплекса. Структуру и конкретное задание по конечной продукции для личных, и общественных нужд комплекса будем считать известными. Структура потребления, вообще говоря, это отдельная проблема, которая должна решаться совместно с производственным планом и также с помощью математических средств, но мы в целях упрощения отвлекаемся от ее анализа.

Составить комплекс планов - значит разработать такие планы для всех предприятий, в которых учитываются имеющиеся ресурсы, заданная для всего комплекса конечная продукция и взаимосогласование выпуска этой продукции по отдельным предприятиям. В плане комплекса, таким образом, должны быть предусмотрены сбалансированные материальные потоки между предприятиями, каждое из которых снабжается необходимыми затрачиваемыми ингредиентами за счет продукции других предприятий или из ресурсов всего комплекса. Кроме того, этот план должен быть оптимальным в смысле одного из возможных критериев.

Анализ такой задачи, которая также сводится к линейно-программной схеме, приводит к следующим условиям оптимальности комплекса. Во-первых, план каждого предприятия сам по себе должен быть оптимальным с учетом (при фиксации) тех входных и выходных потоков, которые предусмотрены связями комплекса. Во-вторых, в системе оценок оптимального плана каждого предприятия оценки внешних ингредиентов (участвующих в разных предприятиях) должны быть одни и те же, т. е. при оптимальном плане комплекса разные предприятия должны оценивать одни и те же ингредиенты одинаково.

Эти условия дают и эффективный способ расчета плана подобного комплекса. Строя оптимальный план для каждого предприятия исходя из некоторой системы оценок для внешних ингредиентов (общих для комплекса), можно скорректировать оценки с тем, чтобы выровнять баланс по соответствующим ингредиентам (снижаем оценку, если тот или иной ингредиент избыточен, и повышаем, если он недостаточен). После ряда исправлений приходим к сбалансированному и оптимальному плану. На этой экономической идее, реализованной в виде точного алгорифма, основан так называемый метод декомпозиции Данцига - Вульфа, который по принципу своего действия напоминает рыночный механизм - избыток ведет к снижению цены и уменьшению выпуска продукта, недостаток вызывает противоположные последствия так, что после некоторого числа шагов устанавливается равновесие. Причем при построении оптимального плана этот механизм реализуется на вычислительной машине, что намного быстрее и, главное, экономнее, нежели реальный рынок.

Наряду с составлением плана комплекса возникает проблема оперативного регулирования деятельности как комплекса в целом, так и отдельных предприятий, обеспечивающего эффективное выполнение плана. Эта научная проблема функционирования экономической системы в оптимальном режиме лишь сравнительно недавно поставлена на повестку дня в полном объеме. Одна из ее важнейших сторон состоит в том, чтобы правильно согласовать оценки деятельности всего комплекса и отдельных его частей.

Действительно, каждое предприятие комплекса имеет свой локальный критерий качества работы, к достижению которого оно и стремится. Если эти локальные критерии не соответствуют общему, глобальному критерию качества работы комплекса, то может случиться, что предприятия, стремясь к улучшению показателей своей деятельности, не способствуют улучшению показателя, характеризующего работу комплекса в целом. Для построения локальных и глобальных критериев могут служить экономические показатели, построенные на базе оценок оптимального плана - прибыль, плата за фонды и др. Характерно, что именно модельный подход открывает пути для эффективного формирования этих критериев.

При составлении производственного плана для большого комплекса приходится считаться и с объемом информации, циркулирующей между отдельными его звеньями. Едва ли целесообразен и возможен обмен всей Детализированной информацией между ними. Естественными представляются планирование и отчетность по достаточно укрупненным, обозримым данным. В противном случае количество лиц, формирующих отчетные и плановые показатели, было бы сравнимо с количеством работников производственной сферы. В связи с этим возникает вопрос об оптимальном агрегировании (объединении в группы пунктов производства, типов сортамента и других видов информации), ставящем своей целью устранение избыточности информации при сохранении, однако, уровня ее, обеспечивающего нормальное функционирование комплекса. Немалую роль такое агрегирование и связанное с ним упрощение задачи планирования сыграет и в расширении возможностей решения подобных задач на ЭВМ.

Упомянутые вопросы, конечно, ни в коей мере не исчерпывают всех проблем, связанных с оптимальным функционированием производственного комплекса. Список их можно было бы продолжить, что мы отчасти и сделаем в последней главе этой книги. Здесь же отметим лишь, что модельный математический подход в сочетании с обобщением практического опыта дает возможность для широкой научной постановки и анализа проблемы оптимального функционирования экономической системы.

Задачи перспективного планирования (динамическая модель). Проблемы перспективного планирования, как указывалось, имеют качественно иной характер, нежели вопросы текущего планирования. Однако для их решения используется тот же аппарат линейного программирования. При перспективном планировании длительный период разбивается на ряд временных интервалов, которые позволяют учесть динамику процесса. Такая динамическая модель учитывает те же ингредиенты, что и статическая модель текущего планирования, однако для каждого временного интервал а они рассматриваются как различные (ведь, например, уголь, добытый в 1972 г., нельзя сжечь в 1971!). В результате число ингредиентов резко возрастает.

То же относится и к производственным способам. Наряду с прежними видами способов, действующими в пределах одного временного интервала, появляются способы, затрагивающие ряд интервалов, например строительство предприятия и последующее его использование. Возможность создания новых средств производства позволяет вводить на последующих этапах новую технологию, учитывать достижения технического прогресса, что чрезвычайно увеличивает число возможных технологических способов производства и приводит к появлению разных вариантов решений.

Постановка задачи перспективного планирования имеет сходный вид с задачей текущего планирования, однако с меньшим числом ограничений. Они относятся к запасам и оборудованию в начальный момент и лишь к немногим ресурсам на весь период (демографические ограничения по ресурсам труда, геологические ограничения по природным ресурсам). Что касается развития производственных фондов, состава продукции, то они определяются в самом плане. Критерием оптимальности является математически оформленное требование наилучшего удовлетворения потребностей в течение планируемого периода и обеспечение потенциальных возможностей дальнейшего роста производства за пределами планового периода. Поскольку при такой постановке задачи получается линейно-программная модель, ее сопровождает двойственная задача и определяются оценки для всех ингредиентов (свои для каждого периода). Таким образом, модель задачи перспективного планирования дает возможность объективно сравнивать не только разнокачественные, но и разновременные затраты и эффекты, приводя их к одному временному интервалу.

Кроме такой, общей динамической модели существуют модели развития отрасли, модели с более стандартизированной структурой способов (модель Неймана), с крупноагрегированными ингредиентами (однопродуктовая и двухпродуктовая модели) и др. Они допускают более упрошенный расчет и анализ. Следовательно, и для решения проблем перспективного планирования разработаны оптимальные математические модели. Некоторые из них исследованы довольно глубоко с качественной точки зрения, но их применение для практических количественных измерений еще встречается со значительными трудностями и нерешенными проблемами.

Сопоставляя динамическую модель со статической моделью, можно отметить ряд преимуществ первой, ее гораздо большую близость к реальной действительности. В статической модели предусматривается задание по выпуску конечной продукции. С одной стороны, оно ограничивает возможности варьирования производственного плана, с другой - реально указать это задание (в части производства средств производства) можно лишь зная план последующего развития экономики. Это значит, что большой объем информации задается "сверху" из внемодельных соображений, чем, естественно, снижается ценность результатов. В динамической же модели задание извне указывается только по предметам потребления, а программа по средствам производства определяется в самом процессе построения плана. Моделям текущего планирования присуща значительная неустойчивость оценок, а также большое число нулевых оценок на ингредиенты. Это связано с тем, что такие ингредиенты кажутся полученными в избытке, поскольку статическая модель не учитывает возможности их использования за пределами планового года. В динамической модели подобные недостатки проявляются намного слабее. Продукт, произведенный в избытке, как правило, имеет ненулевую оценку, так как наряду с прочими способами в модели имеется и "способ хранения".

Следует сказать, однако, что недостатки статической модели в полной мере проявляются, если рассматривать ее как самостоятельную модель. Если же рассматривать ее как фрагмент, часть динамического плана, охватывающую один период, ресурсы и задания которого согласованы с этим планом, то статическая модель лишается указанных недостатков. В качестве иллюстрации рассмотрим задачу составления перспективного плана в весьма упрощенных условиях.

При производстве некоторого продукта используется определенное оборудование одного вида (машины) и трудовые ресурсы. Имеется несколько технологических способов, использующих машины и трудовые ресурсы с разной интенсивностью. Производимый продукт частично расходуется на потребление, а частично - для изготовления или приобретения новых машин. На каждый год известны ресурсы труда, объемы потребления, а также известно число машин, имеющихся в первый год. Необходимо составить производственный план, который, удовлетворяя имеющимся ограничениям, обеспечивал бы максимальный объем производственных мощностей к концу периода. Предполагается при этом, что лицо, составляющее план, располагает следующей информацией.

1. Планируемый период - 4 года.

2. Даны ресурсы труда и объемы потребления (табл. 17).

Таблица 17

3. Указаны текущие (одногодичные) технологические способы (табл. 18).

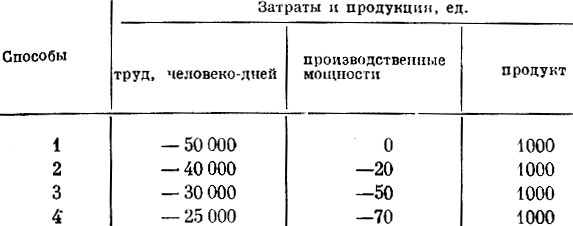
Таблица 18

4. Машины могут приобретаться в любом количестве из расчета 20 единиц продукции за машину. Приобретение и использование машин может быть описано как некоторые способы, реализуемые в течение ряда лет (табл. 19).

Таблица 19

5. В первом году имеется 30 машин.

В табл. 20 приведен оптимальный перспективный план, соответствующий указанным условиям. По этому плану к концу четвертого года машинный парк будет состоять из 271 машины. Чтобы рассчитать такой план, достаточно свести задачу к основной задаче линейного программирования и применить какой-либо из способов ее решения. При этом будет найден план (интенсивности способов), который обеспечивает при заданных ограничениях на ресурсы техники и рабочей силы, а также известных размерах потребления, наибольшие выходные производственные мощности.

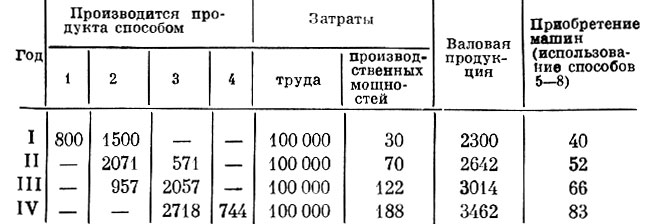
Таблица 20

Убедимся в том, что приведенный план оптимален. Для этого построим о. о. оценки единицы труда, единицы продукта и прокатную оценку машины для каждого из четырех лет. Обозначим их соответственно Т₁, Т₂, Т₃, Т₄ (оценки труда), Р₁, Р₂, Р₃, Р₄ (оценки продукта), М₁, М₂, М₃, М₄ (прокатные оценки машины).

Пусть оценка единицы труда в четвертом году равна А, т. е. Т₄=А. Так как оценка продукции равна сумме оценок затрат и эта сумма одинакова для всех используемых способов, то для оценок справедливы равенства

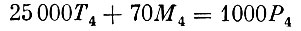
(первый член этой формулы - оценка затрат труда в способе 4; второй - оценка затрат мощностей в способе 4; третий - оценка продукции, полученной по способу 4).

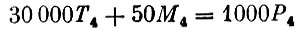
первый член этой формулы - оценка затрат труда в способе 3; второй - оценка затрат мощностей в способе 3; третий - оценка продукции, полученной по способу 3).

Выполняя преобразования, получаем

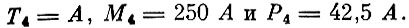
Перейдем теперь к оценкам третьего года. В каждом году оценка машины равна 20 Р. В то же время оценка машины в третьем году разнится от ее же оценки в четвертом году на величину прокатной оценки четвертого года, т. е. можно записать

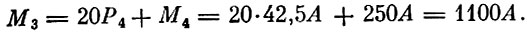
Отсюда сразу следует, что

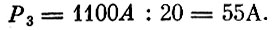
Рассуждая аналогично, можно найти оценки второго, а затем и первого годов. Все оценки приведем к одному периоду, например первому году, при этом величину 4 выберем так, чтобы в первом году оценка единицы продукта равнялась бы единице. Окончательные значения оценок сведены в табл. 21. Легко проверить, что для всех способов оценка продукции не превосходит оценки затрат, а для используемых в плане способов эти оценки совпадают. Ясно, следовательно, что найденные оценки являются о. о. оценками, а приведенный план оптимален.

Таблица 21

В последнем столбце табл. 21 для каждого года, кроме последнего, указана норма эффективности - приращение продукта, которое получается за счет дополнительной единицы продукта, направляемой на накопления. Поясним смысл этого понятия на нашей модели. То обстоятельство, что нормальная эффективность равна, например, 36% в первый год, означает, что выделение дополнительно 100 единиц продукции для вложений в первом году даст увеличение продукции на 136 единиц. Можно сказать, что норма эффективности служит мерой целесообразности затрат продукции на расширение производства - в каждом году осуществляются лишь те вложения, эффективность которых не ниже нормы эффективности соответствующего года. Точнее говоря, выбирая последовательно вложения по их эффективности (от больших к меньшим), мы придем к оптимальному плану.

В применении к динамической модели народного хозяйства, хотя бы и очень укрупненной, этот норматив играет колоссальную роль. Он характеризует эффективность свободных, еще не реализованных капиталовложений и позволяет учесть роль фактора времени в экономике (эти аспекты нормы эффективности будут рассмотрены в последующих главах более подробно).

Итак, мы установили, что оптимальный план характеризуется системой обусловленных оценок трудовых ресурсов, продукции и производственных мощностей (различных для каждого периода), с учетом которых производственные способы, используемые в оптимальном плане, должны быть оправданными. Такие оценки взаимосвязаны и с их помощью можно сравнивать как разнокачественные, так и разновременные затраты и эффекты. В соответствии с этим и все производственные способы (рассчитанные на ряд периодов), которые используются в оптимальном плане, "оправданы" и рентабельны, а неиспользуемые - не более чем оправданы.

Справедливым является следующий общий вывод. Если для данного плана построена характеризующая его динамическая система оценок, то для суждения о целесообразности применения некоторого производственного способа, рассчитанного на ряд периодов (обычно связанного с капиталовложениями), достаточно сопоставить для него ожидаемую за все время продукцию и плановые затраты, приведя их согласно динамической системе оценок к одному периоду. Можно также произвести подсчет продукции и затрат, исходя из оценок каждого периода, и осуществить затем приведение полученных данных к одному периоду согласно коэффициентам приведения или нормам эффективности. Этот вывод играет огромную роль при построении оптимального плана для задачи перспективного планирования.