2. Простейшая линейно-программная модель - задача о раскрое

Знакомство с новым разделом прикладной математики лучше всего начать с описания элементарной экономической задачи. Это позволит разъяснить все необходимые новые понятия и сущность методов линейного программирования. Но прежде - небольшая общая характеристика этого раздела математической экономики и несколько специальных терминов.

Как правило, всякой задаче поиска решения в экономике сопоставляется целевая функция, позволяющая количественно сравнивать возможные решения, оценивать их. Возникающие естественным образом при поиске оптимального решения задачи, в которых отыскивается максимум или минимум целевой функции при наличии ограничений на переменные, объединяются общим названием - задачи математического программирования.

Наряду с термином решение в математическом программировании употребляются в том же смысле термины план, стратегия, управление, поведение. Всякий набор значений переменных, удовлетворяющий ограничениям задачи, носит название допустимого плана. Тот же допустимый план, на котором достигается экстремум (максимум или минимум) целевой функции, называется оптимальным планом.

Все задачи математического оптимального программирования в зависимости от вида целевой функции и ограничений могут быть разбиты на ряд классов так, что каждый класс характеризуется своими методами решения входящих в него задач. Знакомство с этими классами начнем с наиболее изученного из них - класса, в котором и целевые функции задач, и ограничения линейны. Этот круг задач в совокупности с методами отыскания оптимальных решений в них носит название линейного программирования.

Основной идеей линейно-программной модели является рассмотрение производственного плана как составленного из элементарных производственных способов. В этой модели принята гипотеза линейности. Суть ее в том, что каждый производственный процесс предполагается возможным применять с любой кратностью (интенсивностью) и при этом затраты и выход продукции меняются пропорционально; результаты процессов суммируются. В силу такой гипотезы всякий план можно представить в виде набора некоторого числа основных способов, примененных с различными интенсивностями. В ходе решения интенсивности определяются так, чтобы ограничения были удовлетворены, а целевая функция достигала максимума или минимума.

Сделав эти предварительные замечания, перейдем к рассмотрению конкретной задачи о раскрое. Листы материала размером 6·13 м² нужно раскроить так, чтобы получились заготовки двух типов: 800 шт. заготовок типа А (4·5 м²) и 400 шт. типа В (2·3 м²), израсходовав при этом как можно меньше материала. (Для решения такой задачи, конечно, не нужна специальная теория. Но эта задача используется в книге как пример, на котором разъясняются методы линейного программирования).

На рис. 1 изображены исходные листы материала и выкраиваемые из них заготовки. Каждый лист можно раскраивать различными более или менее удачными способами, получая соответственно больше или меньше различных заготовок.

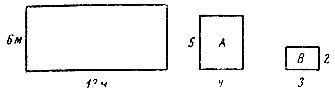
Рис. 1

На рис. 2 приведены некоторые из возможных способов раскроя, причем в скобках указано, сколько заготовок получается из каждого листа: первая цифра - тип А, вторая - тип Б, а числа r_i обозначают потери материала при каждом способе. Раскроить подобным образом можно было бы без всякой математики. А вот какие из способов использовать и для какого числа листов их применить - это вопрос, при решении которого без математики не обойтись. Ведь просмотреть все мыслимые варианты, комбинации способов и выбрать из них наилучший - задача, которая, например, при двадцати типах заготовок не может быть решена и современными ЭВМ.

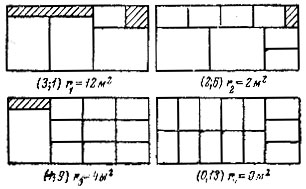
Рис. 2

Переходим к математическому описанию задачи.

Обозначим через x_i число листов материала, раскраиваемых по i-му способу. Пусть a_i и b_i обозначают соответственно число заготовок типа А и В, получаемых при использовании i-й карты раскроя. Например, для первой карты a₁=3, b₁=1, а вся матрица способов имеет вид:

Таблица 1

Используя введенные обозначения, можно дать теперь такую математическую формулировку интересующей нас задачи: найти минимум линейной функции, выражающей число израсходованных листов материала (по всем способам),

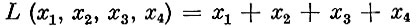
при условии, что переменные x_i удовлетворяют следующим ограничениям:

(1)

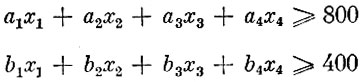
или, подставляя числовые значения (см. табл. 1),

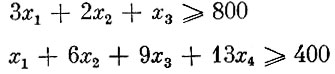
(экономический смысл ограничений (1): соблюдена комплектность - все необходимые заготовки сделаны в достаточном числе).

(2)

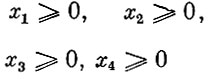
(экономический смысл ограничений (2): ни один способ не применяется к отрицательному числу листов материала, так как физически это означало бы, что из заготовок делаются целые листы).

Это характерные условия задачи линейного программирования: найти минимум (максимум) линейной формы (функции) при линейных ограничениях.

Сделаем следующее вспомогательное построение (рис. 3). В прямоугольной системе координат XOY каждому возможному раскрою сопоставим точку, у которой координата x равна числу заготовок типа А, получаемых при этом раскрое, а координата y - числу заготовок типа B. Эти точки обозначены буквой M с индексом, указывающим номер раскроя. Например, первому раскрою соответствует точка M₁ с координатами x₁=3, y₁=1.

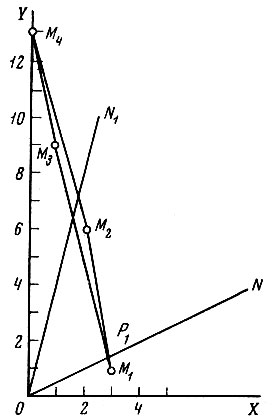
Рис. 3

Точки на отрезке M₁M₂ указывают своими координатами количество заготовок типа А и типа В, приходящихся в среднем на один лист материала в различных планах раскроя, которые представляют собой сочетания раскроев М₁ и М₂. Можно доказать, что множество всевозможных планов раскроя, являющихся комбинациями М₁, М₂, М₃ и М₄, если их характеризовать выходами заготовок, приходящихся на один лист, изображается совокупностью точек выпуклого многоугольника М₁М₂М₄М₃ который называется многоугольником осуществимых планов. Обычно для удобства в число вершин многоугольника осуществимых планов включают и начало координат, так что в окончательном виде такой многоугольник имеет вид ОМ₁М₂М₄. (Экономически это соответствует тому, что осуществимым считается также план, в котором часть полученных заготовок остается неиспользованной.)

Нас интересуют прежде всего те осуществимые планы, Для которых выполнено условие комплектности. В них отношение числа заготовок типа А к числу заготовок типа В соответствует заданному, т. е. равняется 2(800:400). На рис. 3 эти планы изображаются точками, лежащими на луче N. Такие планы называются ассортиментными. Ассортиментному выпуску соответствует допустимый план (для которого выполнены все ограничения 1 и 2). Из ассортиментных планов раскроя выбирается оптимальный план. Ему соответствует точка, принадлежащая одновременно многоугольнику и лучу и имеющая наибольшие координаты, т. е. соответствующая плану, дающему наибольший выход заготовок в данной пропорции на один лист. Такой является точка P₁ - точка пересечения луча с границей многоугольника ОМ₁М₂М₄. Так как точка P₁ принадлежит отрезку М₁М₂, можно сделать заключение, что оптимальный план представляется комбинацией раскроев М₁ и М₂.

Обозначим через z ту долю материала, которая кроится по раскрою М₁; остальная часть 1 - z кроится по М₂. Из условия комплектности (табл. 1) следует, что

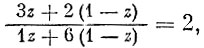
откуда 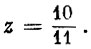Этот результат можно было получить и графически, измерив отрезки М₁М₂ и М₂P₁ (см. рис. 3) и заметив, что

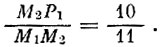
Искомое минимальное число листов материала L находится, например, из условия получения нужного числа заготовок А.

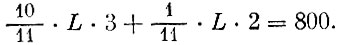
(Экономический смысл этой формулы таков: первый раскрой применяется 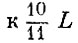листов, при этом из каждого листа получается три заготовки типа А. Второй раскрой применяется 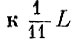листов, при этом из каждого листа получается две заготовки типа А. Общее число заготовок типа А должно соответствовать плановому заданию, т. е. равняться 800.)

Решая уравнение, получаем, что необходимое (минимальное) число листов материала

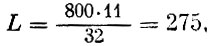
Иначе говоря, оптимальный план раскроя состоит в том, что 250 листов кроятся по первому раскрою (x₁=250), а 25 листов - по второму раскрою (x₂=25).

Любой другой план раскроя оказался бы неоптимальным. Для примера в табл. 2 приведены два плана (первый - с использованием только способа 1, второй - только способа 3), составленных на "глаз", и оптимальный план.

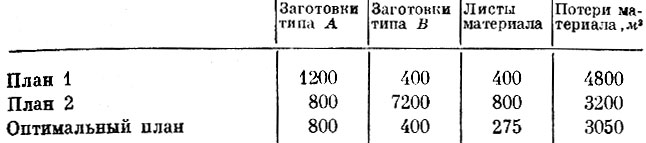
Таблица 2

Если бы количество заготовок было больше двух, то графический способ решения (рис. 3) оказался бы практически трудно реализуемым. Дело в том, что для изображения множества осуществимых планов нужно построить очень сложную геометрическую фигуру - многогранник в многомерном пространстве. Поэтому для решения задачи более рационально использовать аналитические методы и, в частности, эффективный метод разрешающих множителей - оценок, особых показателей, характеризующих оптимальный план.

Что же такое оценки? Это некоторые условные цены для единицы каждого вида продукции и затрачиваемых производственных факторов (например, в данной задаче продукция - заготовки типов А и В, а производственный фактор - листы материала), связанные с оптимальным планом, объективно обусловленные им. Поэтому такие оценки получили название объективно обусловленных, или сокращенно о. о. оценок.

С помощью о. о. оценок удается сформулировать признак оптимальности решения задачи линейного программирования, оказывается возможным выяснить, оптимален ли некоторый допустимый план без сравнения его со всеми остальными возможными планами. Если не вдаваться в математические детали, то экономический смысл признака оптимальности состоит в следующем: для оптимального плана всегда имеются такие оценки, что скалькулированная по ним результативная эффективность способа равна нулю для используемых способов и не может быть более нуля для неиспользуемых. Иначе говоря, все используемые способы оправданы, рентабельны (результаты оправдывают затраты), а во всех отброшенных способах оценка затрат не меньше оценки произведенной продукции, т. е. их применение нерентабельно или во всяком случае не более рентабельно, чем применяемых способов.

Вернемся к нашей задаче и на ней поясним значение о. о. оценок. Покажем, как их находят и как с их помощью можно убедиться, что найденный план (250 листов кроятся по первому способу, а 25 - по второму) действительно оптимален. Введем условные цены - оценки для одного листа раскраиваемого материала и для каждой из заготовок, обозначив их соответственно через U, V, W. Нужно найти такие значения этих величин, при которых используемые способы окажутся рентабельными, а остальные не более рентабельными, чем применяемые. Если это удастся сделать - план оптимален.

В соответствии с изложенным выше смыслом о. о. оценок условия рентабельности запишутся так:

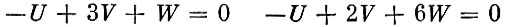
(экономическое значение этих условий можно разъяснить на примере первого из них: затраты одного листа материала с оценкой U должны компенсироваться полученными результатами при раскрое по способу М₁ - тремя заготовками типа А по оценке V и одной заготовкой типа В по оценке W).

Так как два уравнения содержат три неизвестных, то значение одного из них можно выбрать произвольно (важно соотношение оценок, а не их абсолютное значение). Примем U=16. Тогда легко получить V=5, а W=1. Сумма оценок заготовок, получаемых из одного листа материала, в каждом из двух применяемых раскроев одинакова и равна 16. Если же мы возьмем неиспользованные производственные способы 3 и 4 (табл. 1), то для них оценка продукции составит 14 и 13, т. е. будет меньше 16, ниже оценки затрат. Следовательно, данный план допустим и имеются согласованные с ним оценки. Это значит, согласно высказанному общему критерию оптимальности плана, что более экономного плана быть не может.

В справедливости последнего утверждения можно убедиться, рассуждая следующим образом. Предположим, имеется какой-то другой план раскроя, дающий те же нужные заготовки. Если просматривать раскроенные листы и записывать по пять единиц за каждую заготовку А и по единице за заготовку В, общая сумма составит не меньше 800·5+400·1, т. е. 4400. С другой стороны, при добавлении каждого листа прирост этой суммы составит не больше 16, так как сумма оценок заготовок не превосходит 16 ни при одном из раскроев. Значит, число листов не может быть меньше 275(4400:16), т. е. оно не меньше того числа листов, которое расходуется при выбранном плане, являющемся, таким образом, оптимальным. Дальше будет приведено и аналитическое доказательство этого факта в общем случае.

Отметим, что эти оценки имеют и простой геометрический смысл, который позволяет дополнительно пояснить наш критерий. Уравнение прямой М₁М₂ на рис. 3 может быть записано как

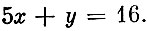
Коэффициенты этого уравнения совпадают с оценками заготовок, свободный член равен сумме оценок заготовок, получаемых из одного листа в используемых раскроях. Таким образом, для плана, скомпонованного из раскроев М₁ и М₂, выход заготовок изображается точкой отрезка М₁М₂, а суммарная оценка продукции, приходящейся на один лист, равна 16. Если бы план включал какой-нибудь иной раскрой, то этому плану соответствовала бы точка ниже прямой М₁М₂ и оценка продукции, приходящейся на один лист, оказалась бы меньше 16. Это свидетельствует об оптимальности плана, составленного из раскроев М₁ и М₂.

Обратим внимание еще на одно обстоятельство. Так как наклон прямой связан с оценками заготовок, это значит, что при передвижении по отрезку М₁М₂ (при переходе от одного оптимального плана к другому) соотношение заготовок изменяется: заготовки А заменяются заготовками В в соответствии с их объективно обусловленными оценками (о. о. оценками) в пропорции 1:5. При существенно иной пропорции заготовок в задании решение определялось бы крайней точкой многоугольника на Другом луче. Оно было бы скомпоновано из других раскроев, и в соответствии с этим мы имели бы опорную прямую с другим наклоном и соответственно другое соотношение оценок для заготовок А и В. Например, если заменить задание, потребовав, чтобы заготовок типа А было выпущено 400, а типа В - 1600, то ассортиментные планы геометрически изобразятся лучом ON₁ (см. рис. 3).

Приведенный критерий, таким образом, обеспечивает возможность проверить "оптимальность" данного плана, не сопоставляя его с другими планами. Достаточно построить для него оценки и по ним сравнить продукцию и затраты во всех способах. Если окажется, что план не оптимален, будет видно, какие изменения нужно внести, чтобы его улучшить.

Казалось бы, из геометрической интерпретации сразу виден способ решения задач линейного программирования. Достаточно построить многоугольник осуществимых планов и найти крайнюю точку пересечения луча, изображающего множество ассортиментных планов, с этим многоугольником. Однако если число выкраиваемых заготовок равно n, каждому раскрою соответствует точка n-мерного пространства, а многоугольник осуществимых планов превращается в многогранник в этом n-мерном пространстве. Условия ассортиментности определяют луч в том же пространстве и, стало быть, геометрически задача сводится к очень сложному процессу поиска крайней точки пересечения многогранника с лучом. Таким образом, еще раз подтверждается, что кажущаяся при геометрической интерпретации простота решения задач линейного программирования является обманчивой.

Как же решать задачи линейного программирования с большим числом переменных и ограничений? В основе наиболее эффективных методов, которые предназначены для этой цели, лежит использование упоминавшихся уже о. о. оценок и признака оптимальности решения задачи. Общая схема расчетов начинается с того, что ищется какое-нибудь решение задачи, так называемое первое приближение - некоторый допустимый план. Обычно это удается сделать без особого труда, привлекая на помощь лишь здравый смысл.

Например, в задаче о раскрое допустимый план может быть построен так. Возьмем способ раскроя, при котором получается заготовка типа А, и применим его к такому числу листов, чтобы иметь нужное число заготовок первого типа. Возможно, при этом будет получено и некоторое число заготовок типа В. Если их достаточно, то допустимый план уже найден, если нее нет, то увеличим их количество до необходимого с помощью другого (или этого же) способа раскроя. Получившееся количество листов материала и примененные способы раскроя определяют допустимый план. Если бы заготовок было больше, чем две, то, продолжая последовательно удовлетворять требования по заготовкам каждого типа, мы также пришли бы в конце концов к допустимому плану.

В соответствии с общей схемой расчетов найденный допустимый план проверяется на оптимальность. Если окажется, что для этого плана выполнен критерий оптимальности (могут быть найдены такие неотрицательные оценки каждого вида продукции и производственных факторов, что для технологических способов, используемых в этом плане, алгебраическая сумма затрат и результатов в этих способах равна нулю, а для способов, не включенных в план, эта же сумма меньше или равна нулю), то этот план оптимален. Если же выясняется, что таких оценок не существует, то план наверняка не оптимален и, значит, надо переходить к "лучшему" допустимому плану. Такой переход может, вообще говоря, осуществляться различными методами. Ниже мы даем описание основной идеи одного из них.

Метод последовательного улучшения плана состоит в том, что в план вводится более эффективный неиспользовавшийся ранее способ, за счет которого достигается увеличение выпуска продукции. Этот способ находят в процессе определения оценок. Последовательно вводя такие способы, улучшают план до тех пор, пока не получат оптимальный план.

Чтобы лучше понять сущность метода последователь-го улучшения плана, представьте себе, что из урны, в которой имеется миллион шаров с произвольными номерами, вы хотите извлечь шар с наибольшим номером. Если добиваться этого результата обычным эмпирическим путем, придется чуть ли не 1000000 раз вытаскивать шары из урны, не возвращая их назад. Это адская работа и назначить ее могут только в качестве наказания. Но допустим, что вам помогает... ангел-хранитель, и после каждого очередного извлечения шара с каким-то номером он уничтожает в урне все шары с меньшими номерами. Тогда общее число шаров будет быстро убывать (примерно вдвое после каждого вытаскивания), и для того, чтобы вытащить шар с наибольшим номером, вам потребуется всего 20-30 извлечений. Так вот, ваш ангел-хранитель - это метод последовательного улучшения плана.

Рассмотрим применение этого метода к нашей задаче о раскрое. Допустим, что в качестве начального выбран план, использующий первый и четвертый способы раскроя (см. табл. 1). В нем число листов материала, раскраиваемого каждым из этих способов, составляет (округленно): х₁=267, а х₄=11. Прежде всего убедимся в том, что этот план допустимый, т. е. удовлетворяет поставленным ограничениям. Для этого подставим в него цифры из табл. 1. Получим 3·267=801>800; 1·267+13·11=410>400. Допустимость плана подтверждена.

Далее приступим к проверке плана на оптимальность. Для этого, как и раньше, введем оценки U, V, W соответственно для одного листа материала, первой и второй заготовок. Условия рентабельности в соответствии с табл. 1 запишутся на этот раз следующим образом:

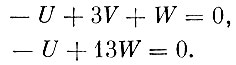
Полагая U=13 (так как имеются два уравнения с тремя неизвестными, то одно неизвестное можно задать произвольно), находим оценки заготовок: V=4 и W=1. Пользуясь ими, оценим продукцию, получаемую при каждом способе раскроя:

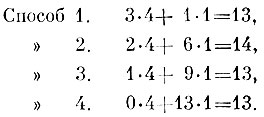
Теперь уже ясно, что рассматриваемый план не оптимален, так как среди неиспользованных оказался способ 2, более рентабельный, чем используемые. Очевидно также и то, как именно план может быть улучшен. Для этого нужно ввести в него второй, наиболее рентабельный способ, исключив, если нужно, один из имеющихся.

Пусть второй способ применяется с интенсивностью Δх₂. Использование нового способа приводит к изменению интенсивностей употреблявшихся ранее способов. Обозначая эти изменения через Δх₁ и Δх₄, запишем условие того, что плановое задание будет выполнено точно. Имеем

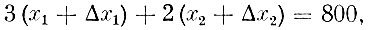
или

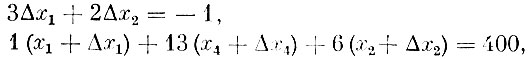
или

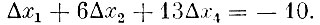
Отсюда следует, что

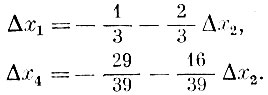
Вновь вводимый способ желательно использовать с наибольшей положительной интенсивностью, по все же такой, чтобы остальные интенсивности остались неотрицательными. При увеличении Δх₂ первой обращается в нуль интенсивность четвертого способа х₄+Δх₄=0, т. е. нужно принять Δх₄=-11. Иными словами, Δх₂ находится из условия

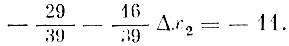
В результате искомые изменения интенсивностей способов равны соответственно

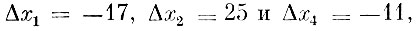
а новый, улучшенный план имеет вид:

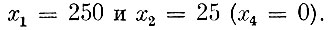
Это тот самый план, оптимальность которого уже была доказана ранее.

Конечно, переход от допустимого плана к оптимальному редко удается осуществить за одно приближение (итерацию), но все же после каждой итерации план улучшается. Получив новый план, мы прежде всего, определяя оценки, выясняем, не оптимален ли он. Если да, то решение заканчивается. Если же нет, то снова применяется метод последовательного улучшения плана. Доказано, что с помощью этого метода за конечное число улучшений можно прийти от любого допустимого плана к оптимальному. И, что самое главное, не просто за конечное, а за разумное число улучшений! Для его реализации на ЭВМ требуются не миллионы лет, а секунды, минуты или на худой конец часы.

Так как в основе метода последовательного улучшения плана лежит использование о. о. оценок и, кроме того, роль этих оценок чрезвычайно велика как в теоретических вопросах математического программирования, так и в вопросах его практического использования, целесообразно более подробно остановиться на изучении их свойств.

Существеннейшей особенностью задач линейного программирования является тот факт, что каждой из них соответствует определенная, тесно связанная с ней другая задача линейного программирования, получившая название двойственной. Оказывается, что упоминавшиеся выше объективно обусловленные оценки единицы каждого вида продукции и затрачиваемых производственных факторов, которые были получены при решении первоначальной задачи на минимум, сами являются решениями некоторой задачи на максимум. Эта сопряженная с нашей задача называется двойственной задачей линейного программирования. Покажем, как естественным образом возникает задача, двойственная к задаче раскроя, и дадим ее экономическую и геометрическую интерпретации.

Чтобы выяснить экономическую суть дела, следует рассмотреть следующую условную ситуацию. Пусть имеется экономическая система, состоящая из двух частей: Завод и Заготовительный цех. Завод для производственных целей заказывает Цеху произвести из листового материала заготовки типов А и В в нужном ассортименте. При этом Завод, естественно, заинтересован, чтобы затраты материала были наименьшими. Выбор способов раскроя, которые обеспечат требуемое количество заготовок при наименьших затратах материала, производится на основе решения задачи линейного программирования, которая уже была рассмотрена выше (будем называть ее прямой задачей). При этом отношения между Заводом и Цехом построены на экономических основах, т. е. Завод оплачивает работу цеха по определенным ценам (на самом деле такое описание экономических отношений чрезвычайно упрощенно, и именно поэтому приведенный пример условен). Какими должны быть эти "цены"? Лучше всего, если они будут обеспечивать наибольшую выгоду обеим сторонам - и Цеху-изготовителю и Заводу-потребителю. Задача отыскания таких "выгодных цен" и есть двойственная задача линейного программирования.

Напомним, что оценки заготовок типов А и В обозначались соответственно через V и W, а оценку исходного листа можно считать равной единице (так выбирается масштаб цен). При использовании первой карты раскроя выкраивается a₁ заготовок типа А и b₁ заготовок типа В. Чтобы цены были оправданными, суммарная оценка продукции не должна превышать оценку исходного листа материала, т. е. должно выполняться неравенство

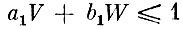
(иначе Заводу было бы невыгодно передавать раскрой Цеху). Аналогичные неравенства должны выполняться и для всех остальных способов. Естественным представляется и другое, уже упоминавшееся требование: оценки следует выбирать так, чтобы суммарная оценка всей произведенной продукции имела максимальную величину.

Используя конкретные числовые значения, приходим к следующей задаче. Найти оценки V и W так, чтобы достигался max {800V+400W}, при условиях

(1′)

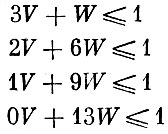
(эти условия означают, что при любом способе раскроя оценка полученных из листа заготовок не превосходит оценки самого листа, т. е. покупать заготовки выгодно);

(2′)

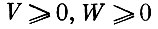
(эти условия означают, что оценки неотрицательны).

Очевидно, что решениями этой задачи являются величины 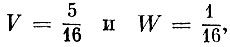т. е. прежние оценки, отнесенные к оценке листа материала. При таких "ценах" Цеху выгодно кроить листы, а Заводу выгодно покупать заготовки.

Двойственная задача имеет такую же простую геометрическую интерпретацию, как и прямая задача. Условия (1′)-(2′) определяют некоторый многоугольник, лежащий в первом квадранте плоскости VOW (рис. 4). Он и является многоугольником допустимых планов двойственной задачи. Уравнение 800V+400W=С определяет прямую линию, проведенную на этой же плоскости. Будем перемещать теперь эту прямую параллельно самой себе, отдаляя от точки О. При этом значение целевой функции будет увеличиваться и достигнет максимума в точке Р. С точки зрения геометрии ясно, что оптимальным решением задачи, как правило, является одна из вершин многоугольника допустимых решений двойственной задачи. Если же окажется две такие вершины, то тогда любая точка соединяющего их отрезка также будет оптимальным решением.

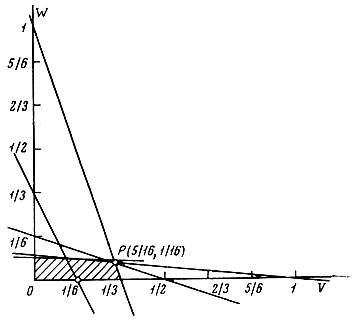
Рис. 4

Использование о. о. оценок лежит в основе не только метода последовательного улучшения плана, о котором мы говорили выше, но и многих других методов решения задач линейного программирования. В качестве примера упомянем метод корректировки оценок. Исходными в этом случае являются приближенные значения оценок, по которым находятся наиболее рентабельные (при этих оценках) способы. Из этих способов формируется план, лишь частично соответствующий заданию или, на языке математики, удовлетворяющий только некоторым ограничениям, т. е. план, который не является допустимым. В нем отдельные виды продукции будут получены в избытке, других же будет не хватать. Затем для тех видов продукции, которые получились в избытке, оценки снижаются, а для тех, которые оказались в недостатке, - повышаются. Соответственно меняется набор рентабельных способов, из которых строится новый план. В конце концов создается допустимый план, а так как одновременно получаются согласованные с ним оценки, то этот план и будет оптимальным.

Высокая эффективность численных методов решения задач способствовала признанию и распространению линейного программирования, обеспечила возможность применения методов линейного программирования для исследования и решения многих практических проблем. Например, вагоноремонтный завод им. Егорова, где рациональный раскрой на основе таких методов был введен более 20 лет назад, до сих пор остается лучшим по использованию металла среди ленинградских заводов. Отметим, что работа, проведенная на этом заводе, является одним из первых в мире практических опытов применения методов линейного программирования. Недавно в Институте математики СО АН СССР и других учреждениях сделаны дальнейшие шаги в развитии методов рационального раскроя с использованием линейного и динамического программирования, а также ЭВМ. Автоматизировано не только комбинирование раскроев, но и нахождение самих карт раскроя.

Характерной особенностью математики является тот факт, что одна и та же математическая задача, одно и то же математическое описание могут применяться в самых разнообразных случаях, для решения разных реальных вопросов. Задача о рациональном раскрое, в частности, также имеет многочисленные применения.

Для многих производств типичным является комплексный (совместный) выпуск нескольких видов продукции при использовании одного и того же исходного сырья и ресурсов: нефтепереработка, плавка полиметаллических руд, разведение мясо-молочного скота и т. д. Во всех этих случаях можно получать конечные продукты в различных пропорциях, подобно тому, как при разных способах раскроя меняются соотношения в числе заготовок. Ясно, что во всех этих случаях применима та же математическая модель, которая использовалась в задаче о раскрое. На ее основе могут быть решены задачи выбора производственных способов, позволяющих получить продукцию нужного состава с наименьшими затратами.

Не менее типичной является ситуация, когда решается вопрос о мере использования каждого из заданных видов продукции для достижения определенной цели. Математическое описание связанных с этих кругом вопросов получило название задач о смесях. Например, для получения легированной стали нужно использовать шихту, удовлетворяющую определенным требованиям относительно химического состава. В зависимости от своих ингредиентов шихта имеет самую разную цену. Поэтому возникает задача о выборе наиболее дешевой шихты, в составе которой имеются необходимые химические вещества в заданных количествах. Второй пример. Бензины разных сортов получаются путем смешивания нефтепродуктов, имеющих различные технические характеристики и разные цены. Задача состоит в том, чтобы построить такой план смешивания нефтепродуктов, который обеспечивал бы максимальную рентабельность производства, позволяя в то же время получать бензины заданных сортов в нужных пропорциях.

Задачи, которые представлены в обоих примерах, могут быть описаны с помощью математических моделей, подобных той, что использовалась в задаче о раскрое. Это показывает, что анализ задачи имеет гораздо большее значение и более широкую область применений, чем может показаться на первый взгляд.

дебетовые карты с бесплатным обслуживанием