Глава III. Стоимость и воспроизводство

Стоимость и ее реализация

Субстанцией стоимости товара, как мы видели, является количество абстрактного человеческого труда, затраченного на его производство. Это не только непосредственно затраченный живой труд, но и труд, воплощенный в сырье, изношенных инструментах и оборудовании. Поэтому стоимость товара определяется не только тем рабочим временем, которое непосредственно необходимо для его производства, но и косвенно необходимым для этого рабочим временем. Однако не существует никакой гарантии, что вся стоимость, созданная таким образом в процессе труда, будет реализована в процессе обращения, т. е. что товар может быть продан по его стоимости.

Общая форма товарного обмена такова: W - G - W'^*. Это означает, что два товара с различными потребительными стоимостями W и W' обмениваются посредством денег. Обмен осуществляется благодаря следующим двум превращениям: превращению товара W в деньги G и превращению денег G в другой товар - W. Первое превращение W - G - это продажа, второе - G - W' - это купля товара. Воспроизводство может осуществляться беспрепятственно только в том случае, когда производство и потребление уравновешивают друг друга и предложение товаров соответствует покупательной способности и потребностям покупателей как в отношении стоимости, так и в отношении потребительной стоимости. Может происходить и перепроизводство, в результате чего товары продаются по ценам ниже их стоимости. С другой стороны, внезапное увеличение спроса может способствовать продаже товаров выше стоимости. Поэтому для беспрепятственного осуществления воспроизводства недостаточно, чтобы на производство продукта каждой отрасли тратилось общественно необходимое рабочее время. Необходимо также такое распределение всего рабочего времени общества между отраслями производства, при котором каждый продукт производится в соответствии с общественным спросом. "Эта количественная граница тех частей общественного рабочего времени, которые можно целесообразно затратить на различные особые сферы производства, есть лишь более развитое выражение закона стоимости вообще, хотя необходимое рабочее время приобретает здесь иной смысл"^**.

^* (Т - Д - Т'. - Прим. ред.)

^** (К. Маркс и Ф. Энгельс. Соч., т. 25, ч. II, с. 186.)

Стоимостное строение продуктов

Как показано в предыдущей главе, условие равновесия состоит в том, что W₁ - стоимость всей продукции I подразделения равна всей величине постоянного капитала С, требующегося для трех подразделений, стоимость продукта II подразделения W₂ равна всему переменному капиталу V, a W₃ - стоимость продукции III подразделения равна всей прибавочной стоимости М. Мы показали, что

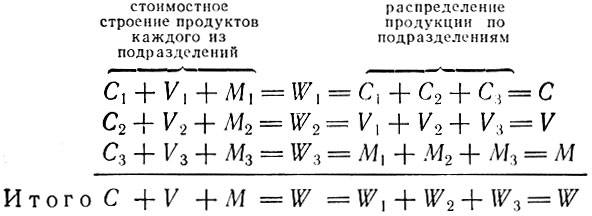
В настоящей главе мы преобразуем эту схему, заменив элементы стоимостного строения продукта их удельными весами. Это позволит применить более тонкий математический инструментарий и изложить метод, который мы применяем в последующих главах. Однако к самой теории ничего не добавлено, так что читатель при желании может ограничиться беглым просмотром этой главы.

Сначала введем некоторые новые обозначения. Пусть α_i - это отношение постоянного капитала С_i к продукту W_i, β_i - отношение переменного капитала V_i к W_i, γ_i - отношение М_i к W_i. Назовем каждую из этих величин отношением стоимость - продукт. Вспомним, что в ходе процесса производства постоянный и переменный капиталы используются полностью и их стоимости переносятся на продукт. Созданная в процессе производства прибавочная стоимость также воплощается в продукте. С помощью указанных относительных величин можно измерять эти компоненты по отношению к продукции каждого подразделения, а именно:

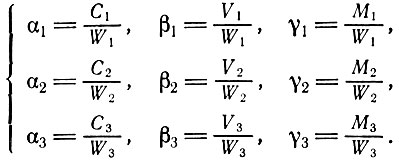(3.1)

Отсюда следует, что

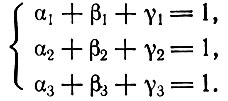(3.2)

Допустим, что отношения стоимость - продукт α_i, β_i и γ_i заданы. Какие соотношения между W₁, W₂ и W₃ обеспечивают непрерывное продолжение воспроизводства? Как и ранее, условия реализации продукции, выпущенной каждым подразделением, выражаются следующим образом:

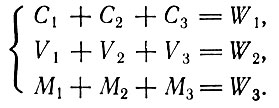(3.3)

Преобразовав эти равенства с помощью соотношений (3.1), получим

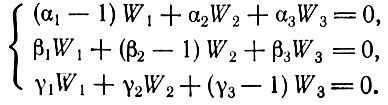(3.4)

Только два из этих трех уравнений являются независимыми, так как третье может быть выведено из них. Возьмем первое и второе уравнения и перепишем их в виде

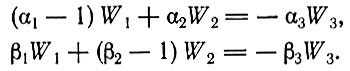
Применяя теперь правило Крамера, получаем

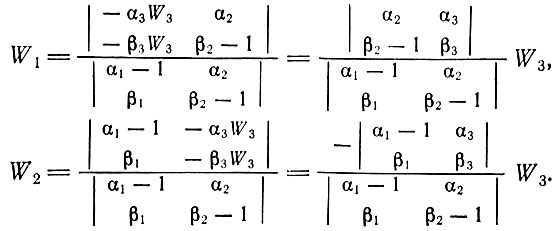
Представим эти соотношения в виде

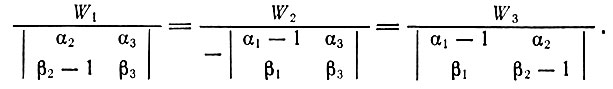(3.5)

Так как строки и столбцы определителя можно поменять местами (транспонировать), не изменяя его величины, то последнее выражение можно записать как

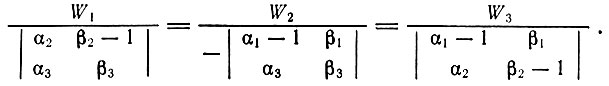(3.6)

Систему уравнений (3.4) можно записать в матричной форме

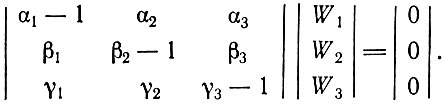
Транспонируя матрицу коэффициентов этой системы уравнений, приходим к следующему выражению для ее определителя:

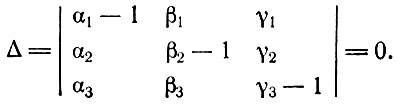(3.7)

Сопоставляя (3.6) и (3.7), мы видим, что каждый из знаменателей в (3.6) представляет собой алгебраическое дополнение одного из элементов третьего столбца определителя Δ^*. Обозначая эти алгебраические дополнения как Δ₁₃, Δ₂₃, Δ₃₃, можно переписать (3.6) в виде

^* (Тем читателям, которые не знакомы с понятием алгебраического дополнения, следует обратиться к любому учебнику, содержащему начала линейной алгебры.)

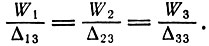(3.8)

Отметим, далее, следующие особые свойства определителя:

а) как показано в (3.7), определитель равен нулю, потому что элементы любого столбца этого определителя становятся равными нулю, если прибавить к ним соответствующие элементы двух других столбцов. Такое преобразование не меняет величины определителя, который равен нулю, так как один столбец в результате преобразования составлен из нулевых элементов;

б) алгебраические дополнения всех элементов какой-либо отдельной строки имеют одно и то же значение:

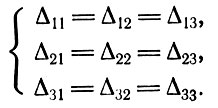(3.9)

Рассмотрим, например, алгебраические дополнения элементов первой строки. Алгебраическое дополнение Δ₁₁ можно преобразовать следующим образом, складывая второй столбец с первым:

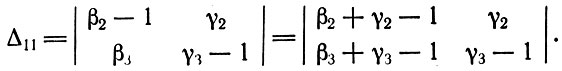
Из (3.2) следует, что β₂ + γ₂ - 1 = -α₂, β₂ + γ₃ - 1 = -α₂. Следовательно,

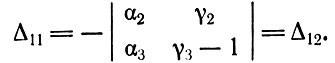
В Δ₁₂ также можно сложить первый столбец со вторым:

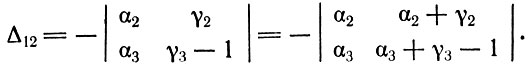
Из (3.2) следует, что α₂ + γ₂ = -(β₂ - 1), α₃ + γ₃ - 1 = -β₂. Следовательно,

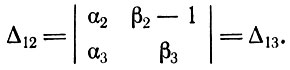
Таким образом, Δ₁₁ = Δ₁₂ = Δ₁₃. Точно так же можно показать, что соответствующие равенства выполняются для алгебраических дополнений к элементам второй и третьей строк.

В соответствии с этим можно записать (3.8) в виде

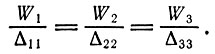(3.10)

Δ₁₁, Δ₂₂, Δ₃₃ называются главными минорами определителя Δ.

Предположим теперь, что стоимость всего совокупного общественного продукта, воплощающая совокупное общественное рабочее время, равна W. Из соотношений (3.8) и (3.10) следует, что беспрепятственное осуществление процесса воспроизводства возможно при следующем распределении всего этого рабочего времени между подразделениями:

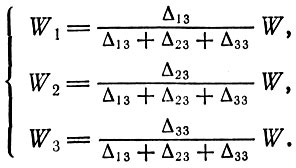(3.11)

Используя (3.9), эти выражения можно записать иначе:

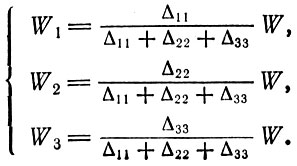(3.12)

Далее, используя отношения стоимость - продукт и величину общественного продукта W, можно определить в составе общественного продукта те величины постоянного капитала С, переменного капитала V и прибавочной стоимости М, которые должны быть направлены в каждое подразделение. Из (3.1) получаем, что

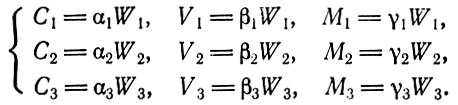(3.13)

Запишем это в матричной форме

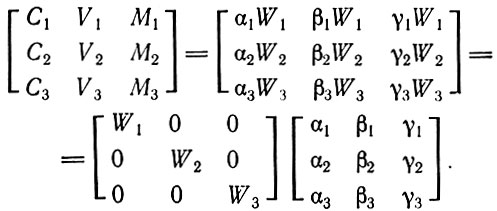(3.14)

Подставляя сюда выражения из (3.12), получаем

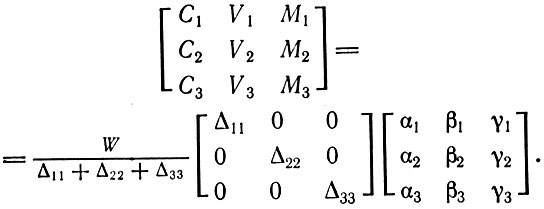(3.15)

Таким образом, если задан совокупный общественный продукт и коэффициенты α_i, β_i, γ_i определяющие стоимостное строение продукции каждого подразделения, то можно установить размеры постоянного капитала С_i, переменного капитала V_i и прибавочной стоимости M_i, которые необходимы для беспрепятственного осуществления простого воспроизводства.

Кроме того, из (3.12) и (3.13) мы получаем

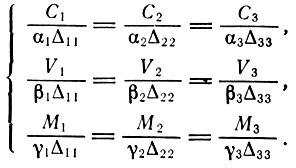(3.16)

Используя эти выражения совместно с условием равновесия при простом воспроизводстве (W₁ = С, W₂ = V, W₃ = М) и с соотношениями (3.10) и (3.13), мы получаем

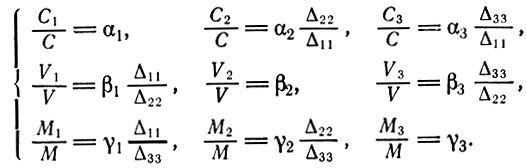(3.17)

Здесь с помощью отношений стоимость - продукт показаны те пропорции, в которых распределены по подразделениям постоянный и переменный капиталы и прибавочная стоимость.

Числовой пример

Для того чтобы пояснить сказанное выше, рассмотрим числовой пример. Допустим, что составные части стоимости продукции находятся в следующих соотношениях:

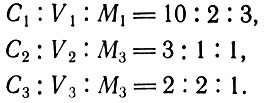
Введенные в (3.1) отношения стоимость - продукт имеют следующие значения:

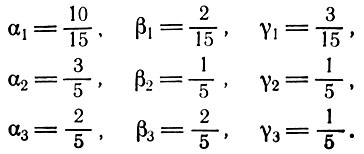
В соответствии с этим

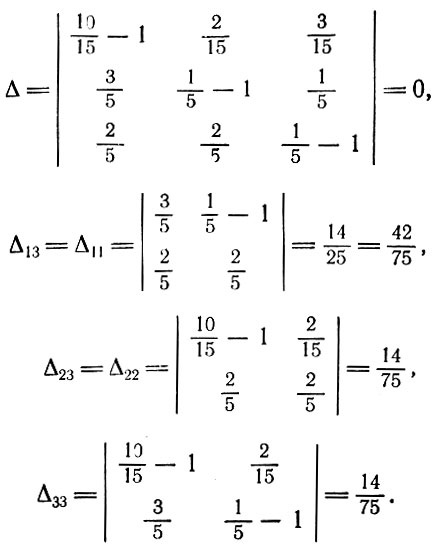
Следовательно, Δ₁₁:Δ₂₂:Δ₃₃ = 3:1:1.

Теперь предположим, что стоимость совокупного общественного продукта W равна 10000. Тогда, согласно (3.15), получаем стоимостное строение для случая простого воспроизводства

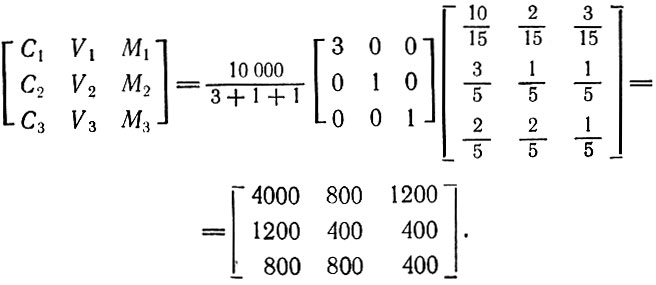
В терминах схем К. Маркса это выглядит следующим образом:

Мы видим, что предложение средств производства 6000w, 2000w товаров, приобретаемых на заработную плату, и предметов роскоши для капиталистов 2000w равно спросу на соответствующий вид благ, так что воспроизводство будет осуществляться беспрепятственно.

Расширенное воспроизводство

Мы выяснили соотношение между стоимостным строением продукции каждого из подразделений и воспроизводственной системой в целом. Теперь обратимся к воспроизводству в расширенном масштабе. Напомним, что для беспрепятственного осуществления процесса расширенного воспроизводства, в котором часть прибавочной стоимости накапливается каждый год в форме капитала, должны выполняться следующие условия: стоимость средств производства, которые I подразделение предлагает к поставке в начале года, равна общему количеству возобновляемого и добавочного постоянного капитала во всех трех подразделениях; стоимость поставляемых II подразделением предметов потребления для рабочих равняется величине возобновляемого и добавочного переменного капитала в трех подразделениях; стоимость поставляемых III подразделением предметов потребления для капиталистов должна равняться первоначальному и добавочному потреблению капиталистов. Это можно записать в следующем виде:

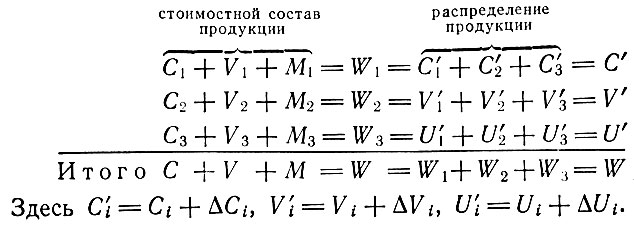
Сравнивая эти выражения с уравнениями для простого воспроизводства, мы видим, что при простом воспроизводстве выпуск продукции каждого подразделения был соответственно равен неизменяющимся величинам постоянного капитала, переменного капитала и прибавочной стоимости. При воспроизводстве в расширенном масштабе выпуски продукции отдельных подразделений равны постоянному капиталу, переменному капиталу и потреблению капиталистов вместе с приращениями этих величин.

Применяя те же действия, что и ранее, запишем исходные значения отношений стоимости к продукту в начале производственного периода:

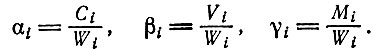(3.18)

Следовательно,

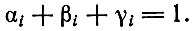(3.19)

В нашем изложении расширенного воспроизводства продукт каждого подразделения представлен в такой форме, где выделены части, используемые соответственно для увеличения С_i, V_i и W_i. Поступая аналогично, обозначим

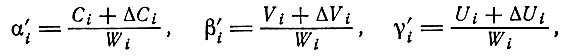
так что

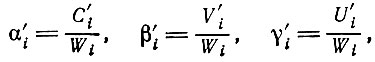(3.20)

где

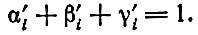(3.21)

Коэффициенты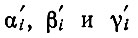  

определяют, как должны увеличиваться размер капитала и потребление капиталистов. Далее, используя условия равновесия

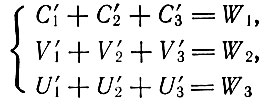(3.22)

совместно с соотношениями (3.20), мы получаем

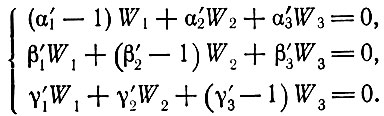(3.23)

Запишем определитель матрицы системы (3.23) после транспонирования

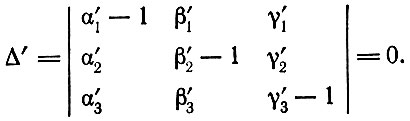(3.24)

Рассуждая так же, как в случае простого воспроизводства, можно представить пропорцию между выпусками продукции в различных подразделениях в следующем виде:

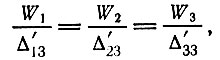(3.25)

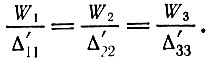(3.26)

Следовательно, при заданной величине стоимости общественного продукта W можно выяснить, как должны быть распределены части этого продукта для того, чтобы обеспечивалось воспроизводство в расширенном масштабе, а именно

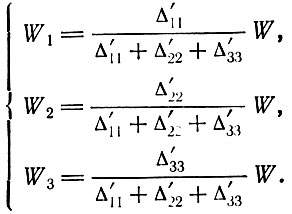(3.27)

Когда размеры выпуска продукции найдены, могут быть определены и величины составных частей стоимости до начала процесса накопления

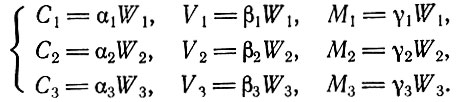(3.28)

В соответствии с (3.27) эти соотношения можно записать в следующем виде:

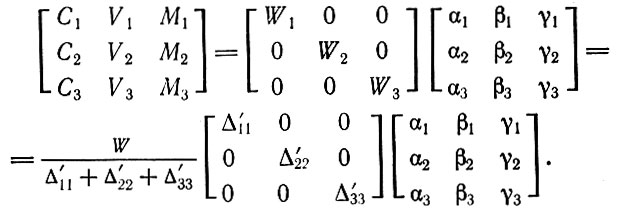(3.29)

Таким образом, исходя из величин стоимости общественного продукта и отношений стоимость - продукт, можно найти размеры постоянного капитала, переменного капитала и прибавочной стоимости в каждом подразделении перед началом очередного цикла накопления. Зная те пропорции, в которых должен накапливаться капитал, а именно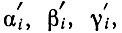  

мы можем получить величины стоимости постоянного и переменного капитала, предназначенного для накопления

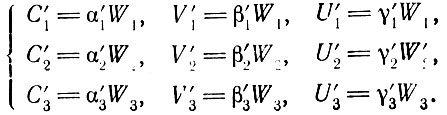(3.30)

Так же как и выше, это можно представить в матричной форме:

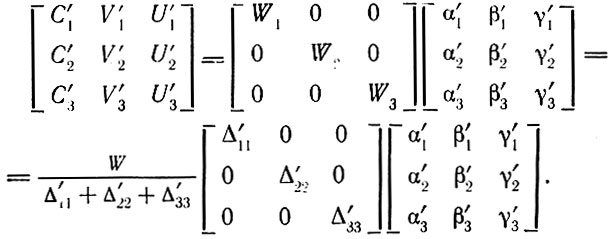(3.31)

Таким образом, зная величину всего общественного продукта и отношения стоимость - продукт, можно найти новые составные части стоимости продукта каждого подразделения.

В заключение исследуем соотношение между первоначальными значениями постоянного и переменного капитала, прибавочной стоимости и стоимостным строением и значениями этих величин при расширенном воспроизводстве. Из (3.29) мы получаем, что

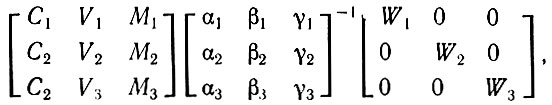
из (3.31) - что

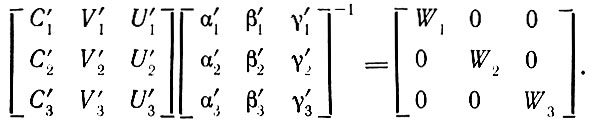
Отсюда следует, что

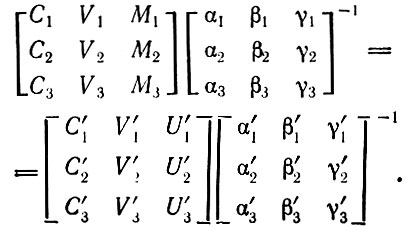(3.32)

Записывая это равенство как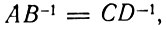  

мы получаем:

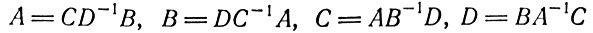
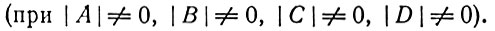
Эти соотношения соответствуют расширенному воспроизводству, если ΔC_i > 0, ΔV_i > 0; если же ΔC_i = 0 и ΔV_i = 0, то они соответствуют простому воспроизводству; в случае ΔV_i < 0 и ΔC_i < 0 эти соотношения выражают процесс, противоположный накоплению. Здесь i = 1, 2, 3.

Числовой пример

Рассмотрим расширенное воспроизводство при следующем стоимостном строении продукции каждого подразделения (до накопления)

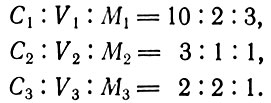
Соответствующие пропорции, видоизмененные при накоплении, таковы:

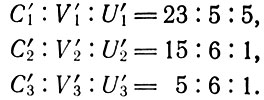
Совокупный общественный продукт W равен 10000. Первоначальные отношения стоимость - продукт

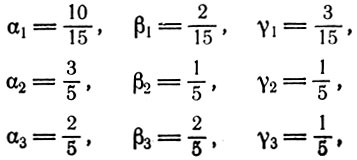
а соответствующие отношения при накоплении составляют

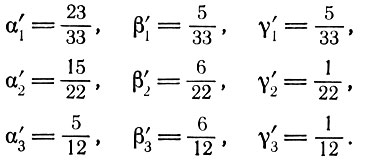
Из (3.29) и (3.31) получаем

Следовательно, модель данного процесса для начала года формируется следующими равенствами:

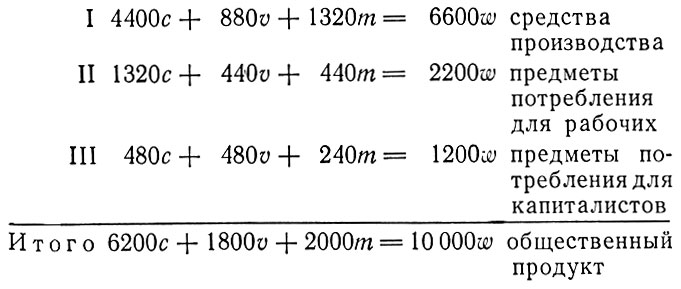
Прибавочная стоимость в каждом подразделении делится в этом примере на прирост постоянного капитала, прирост переменного капитала и часть, предназначенную для потребления капиталистов, в следующих соотношениях:

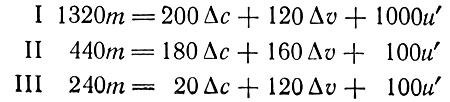
Схема воспроизводства после осуществления накопления приобретает такой вид:

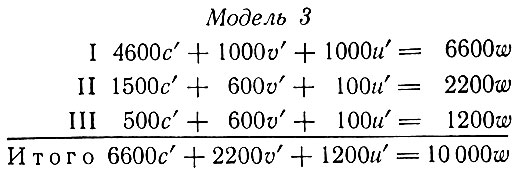
Отметим, что предложение средств производства, составляющее 6600w, равно спросу 6600с', предложение предметов потребления для рабочих 2200w равно спросу 2200u', предложение предметов потребления для капиталистов 1200w равно спросу 1200u', так что в этом году процесс воспроизводства осуществляется беспрепятственно.

Мы показали, как можно представить простое и расширенное воспроизводство с помощью матричных обозначений, и получили некоторое представление о возможностях и изяществе этого метода. В следующей главе мы продвинемся несколько дальше в его разработке.