14.2. Дисконтированная стоимость

Мы вернемся к заводу электродвигателей стоимостью 10 млн. долл. в разделе 14.4, а теперь нам предстоит разобраться с основной проблемой - сколько стоит сегодня 1 долл., выплаченный в будущем. Ответ зависит от ставки процента - нормы, по которой можно получить ссуду или предоставить кредит.

Предположим, что ставка процента равна R. (Пока мы не рассматриваем, какой именно ставкой процента она является. Позднее мы обсудим, как осуществлять выбор между различными видами процентных ставок.) Тогда 1 нынешний доллар может быть инвестирован, чтобы принести 1 + R долларов ровно через год. Следовательно, 1 + R долларов является стоимостью сегодняшнего 1 долл. Какова же нынешняя стоимость, т. е. текущая дисконтированная стоимость (PDV), 1 долл., выплачиваемого через год? Ответ прост, раз мы видим, что 1 + R долларов через год стоят (1 + R):(l + R) = 1 долл. сегодня. Таким образом, 1 долл. через год стоит 1 долл./(1 + R.) сегодня. Это то количество денег, которое даст 1 долл. через год, если он приносит прибыль по учетной ставке R.

Какова сегодня стоимость 1 долл., выплачиваемого через два года? Если бы 1 долл. был вложен сегодня по ставке процента R, он стоил бы 1 + R долл. через год и (1 + R) · (1 + R) = (1 + R)² долл. через два года. Так как (1 + R)² долларов через два года - это стоимость сегодняшнего 1 долл., 1 долл. через два года стоит 1 долл./ (1 + R)² сегодня. Аналогичным образом 1 долл., выплачиваемый через три года, стоит сейчас 1 долл./(1 + R)³, а 1 долл., выплачиваемый через n лет, стоит сегодня 1 долл./(1 + R)ⁿ. Мы можем обобщить все следующим образом:

PDV 1 долл., выплачиваемого через год,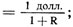

PDV 1 долл., выплачиваемого через два года,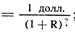

PDV 1 долл., выплачиваемого через три года,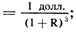

PDV 1 долл., выплачиваемого через n лет,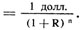

В табл. 14.1 приведена для различных ставок процента текущая дисконтированная стоимость 1 долл., выплачиваемого через 1, 2, 5, 10, 20 и 30 лет. Отметим, что при ставке процента выше 6 или 7 % 1 долл., выплачиваемый через 20 или 30 лет, стоит очень мало сегодня. Но это не так при низких ставках процента. Например, если R составляет 3 %, PDV 1 долл. через 20 лет приблизится к 55 центам. Или иначе: если 55 центов были бы инвестированы сейчас при ставке 3 %, они принесли бы около 1 долл. через 20 лет.

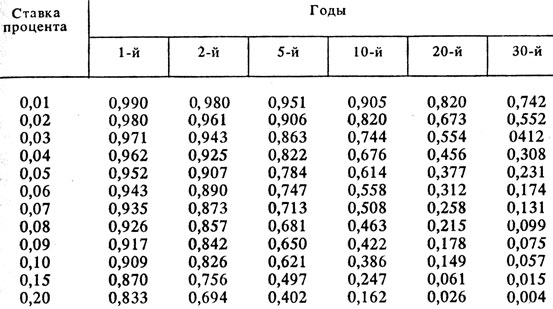
Таблица 14.1. Дисконтированная система 1 долл

Оценка будущих доходов

Мы можем теперь определить дисконтированную величину доходов по времени. Например, рассмотрим два вида дохода в табл. 14.2. Доход А равен 200 долл.: 100 долл., выплачиваемые сейчас, и 100 долл. через год. Доход В равен 220 долл. : 20 долл., выплачиваемые сейчас, 100 долл. - через год и еще 100 долл. через два года. Какой из этих двух доходов вы предпочитаете получить? Ответ зависит от величины ставки процента.

Таблица 14.2. Два вида дисконтированного дохода

Чтобы рассчитать дисконтированную величину этих доходов, мы вычисляем и складываем дисконтируемую величину каждого года выплат:

PDV дохода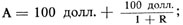

PDV дохода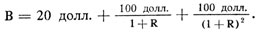

В табл. 14.3 приведена дисконтированная величина обоих доходов при ставках 5, 10, 15 и 20%. Как видно из таблицы, предпочтительность дохода зависит от ставки процента. При ставке 10 % или меньше доход В предпочтительнее дохода А. При ставке 15 % или больше доход А предпочтительнее дохода В. Причина заключается в том, что хотя сумма дохода А меньше, но он выплачивается быстрее.

Таблица 14.3. Расчет величины дисконтированного дохода при различных ставках процента

Пример 14.1. Определение величины убытков

В судебной практике при несчастных случаях пострадавшими или их наследниками (если жертвы погибли) возбуждается дело против нанесшей ущерб стороны (или страховой компании) с целью возмещения ущерба. Кроме компенсации за причиненные боль, страдание и моральные потери, к ущербу относят и будущий доход, который пострадавший или погибший получил бы, не случись несчастья. Чтобы увидеть, как рассчитываются дисконтированные убытки, рассмотрим действительное происшествие 1986 г. (Для сохранения анонимности имена и некоторые данные изменены.)

Харольд Дженнингс скончался 1 января 1986 г. в возрасте 53 лет в результате автомобильной катастрофы. Его семья представила в суд иск против водителя другой машины за преступную небрежность. Семья просила, чтобы основная часть ущерба была возмещена в сумме дисконтированной стоимости доходов г - на Дженнингса, которые он получил бы, работая пилотом авиакомпании, если бы не погиб. Расчет дисконтированной стоимости представляется типичным для подобных случаев.

За 1986 г. его зарплата составила бы 85 000 долл., а возраст выхода на пенсию летного состава равен 60 годам. Чтобы подсчитать дисконтированные убытки г - на Дженнингса, мы должны учесть три аспекта. Во - первых, его сумма дохода, вероятно, возросла бы со временем. Во - вторых, мы не можем быть уверены, что он дожил бы до пенсии, даже если бы не произошел данный несчастный случай. Он мог бы скончаться и по какой - нибудь другой причине. Следовательно, сумма его дисконтируемых убытков вплоть до выхода на пенсию в 1993 г. составляет:

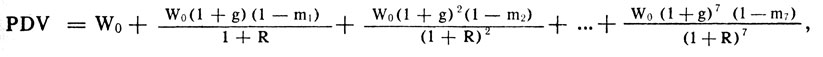
где W₀ - зарплата г - на Дженнингса в 1986 г.; g - вероятный ежегодный процент прироста его зарплаты (так что его зарплата в 1987 г. была бы равна W₀(1 + g) в 1988 г. - W₀ (1 + g)² и т. д.); m₁, m₂, m₃ представляют собой коэффициенты смертности, т. е. вероятности, что он умер бы по какой - нибудь другой причине к 1987, 1988, 1993 г.

Чтобы рассчитать данную PDV, нам необходимо знать коэффициент смертности m₁, ...., m₇, ожидаемые темпы роста зарплаты г - на Дженнингса g и ставку процента R. Данные о смертности можно найти в таблице страхования, которая дает коэффициент смертности для мужчин аналогичного возраста и расы. Величину g мы можем принять равной 8 % - средний темп прироста зарплаты пилотов авиакомпаний за прошедшее десятилетие. Наконец, в качестве ставки процента мы можем использовать ставку государственного займа, которая в 1986 г. составляла 9 %. Табл. 14.4 включает элементы расчета дисконтируемых убытков.

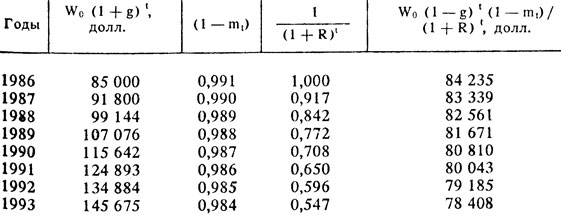
Таблица 14.4. Расчет дисконтированных убытков

Суммируя данные последней колонки, мы получаем убытки в сумме 650 252 долл. Если бы семье г - на Дженнингса удалось доказать, что вина лежит на ответчике, никаких проблем с возмещением ущерба в данном деле не возникло бы, - она могла бы получить эту сумму в качестве компенсации.

оформить кредитную карту