7.3. Издержки на долговременном этапе

На долговременном этапе времени фирма может менять все используемые факторы производства. В данном разделе мы покажем, как руководитель выбирает сочетание факторов производства, которое минимизирует издержки производства определенного объема продукции. Мы также постараемся показать взаимосвязь между долговременными издержками и объемом выпуска продукции.

Выбор факторов производства, минимизирующих издержки

Начнем с рассмотрения фундаментальной проблемы, с которой сталкиваются все фирмы: как выбрать такое сочетание факторов, чтобы достичь определенного объема производства с минимальными издержками. Для упрощения возьмем два переменных фактора: труд (измеряемый в часах работы) и капитал (измеряемый в часах использования машин и оборудования). Мы исходим из предположения, что и труд, и капитал могут быть наняты или арендованы на конкурентных рынках. Цена труда равна ставке зарплаты w, а цена капитала - арендной плате за оборудование r. Мы предполагаем, что капитал "арендуется", а не приобретается, и поэтому можем поставить все деловые решения на сравнительную основу. Например, работники могут наниматься за зарплату 12 000 долл. в год, а капитал "арендоваться" за 75 000 долл. в год.

Так как труд и капитал привлекаются на конкурентной основе, мы принимаем цену этих факторов постоянной. Тогда мы можем сконцентрировать внимание на оптимальном сочетании факторов производства, не беспокоясь, что крупные закупки вызовут скачок в ценах на используемые факторы производства.

Изокоста

Начнем с рассмотрения издержек производства, которые могут быть представлены в виде изокост. Изокоста включает все возможные сочетания труда и капитала, которые имеют одну и ту же суммарную стоимость, т. е. все сочетания двух факторов производства с равными валовыми издержками. Чтобы увидеть, как выглядит изокоста, вспомним, что валовые издержки ТС на производство определенного объема продукции равны сумме издержек на оплату рабочей силы wL и капитальных издержек rК:

Для каждого значения валовых издержек уравнение (7.3) графически выражается отдельной изокостой. Например, изокоста С0 на рис. 7.2 описывает все возможные сочетания факторов производства, приобретение которых обходится в С_o

Если мы перепишем уравнение валовых издержек (7.3) как уравнение для прямой линии, мы получим

Из этого следует, что изокоста имеет угловой коэффициент, равный ΔК/ΔL = - (w/r), что является отношением ставки заработной платы к арендной плате за пользование капиталом. Данный коэффициент аналогичен угловому коэффициенту бюджетной линии, с которой сталкивается потребитель (потому что этот коэффициент определяется ценами товаров: в одном случае ценами факторов производства, в другом - ценами на готовую продукцию). Угловой коэффициент изокосты показывает, что; если фирма отказывается от единицы трудозатрат (и экономит w долларов), чтобы приобрести w/r единиц капитала по цене г долл. за единицу, валовые издержки производства остаются теми же. Например, если ставка зарплаты была бы 10 долл., а арендная плата 5 долл., фирма смогла бы заменить одну единицу труда двумя единицами капитала без каких - либо изменений валовых издержек.

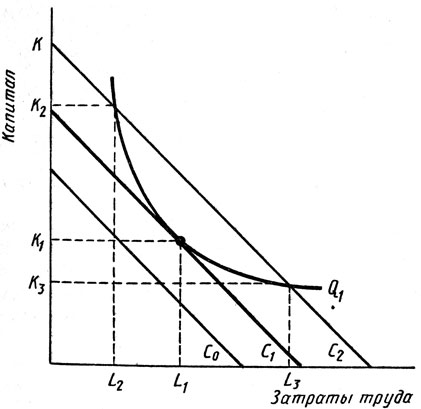
Рис. 7.2. Зависимость объема выпуска продукции от минимальных издержек производства

Выбор факторов производства

Предположим, мы хотим достичь объема выпуска продукции Q₁. Как мы можем сделать это с минимальными издержками? Посмотрите на изокосту на рис. 7.2. Проблема заключается в том, чтобы выбрать точку на данной кривой, которая минимизирует валовые издержки.

Рис. 7.2 показывает решение данной проблемы. Предположим, фирма хотела бы потратить С₀ на приобретение факторов производства. К сожалению, ни одно сочетание факторов, которое позволило бы фирме достичь объем выпуска Q₁, не может быть приобретено за сумму С₀. Выпуск продукции Q₁ может быть достигнут при затратах С₂ с использованием К₂ единиц капитала и L₂ единиц труда либо Кз единиц капитала и L₃ единиц труда. Но С₂ больше минимальных издержек. Тот же выпуск продукции Q₁ может быть достигнут более дешевым способом при издержках C₁ за счет использования K₁ единиц капитала и L₁ единиц труда. Фактически изокоста C₁ является самой нижней, которая допускает выпуск продукции Q₁. Точка касания изокванты Q₁ и изокосты C₁ определяет набор факторов производства L₁ и K₁, минимизирующий издержки. В этой точке углы наклона изокванты и изокосты одинаковы.

Когда затраты по всем факторам производства растут, угол наклона изокосты не меняется (так как цены на факторы производства не изменились), но отрезок изокосты между осями координат увеличивается. Предположим теперь, что цена одного из факторов производства (скажем, труда) возрастает. Тогда угол наклона изокосты - (w/r) увеличивается, а сама кривая становится круче. Это показывает рис. 7.3. Первоначальная изокоста C₁, и фирма минимизирует издержки, производя объем продукции Q₁ в точке А, используя L₁ единиц труда и K₁ единиц капитала. Когда цена труда растет, изокоста становится круче. Кривая С₂ отражает увеличение цены труда. Сталкиваясь с увеличением цены труда, фирма минимизирует свои издержки на выпуск Q₁ единиц продукции в точке В, используя L₂ единиц труда и К₂ единиц капитала. Фирма реагирует на повышение цены труда, заменяя в производственном процессе труд капиталом.

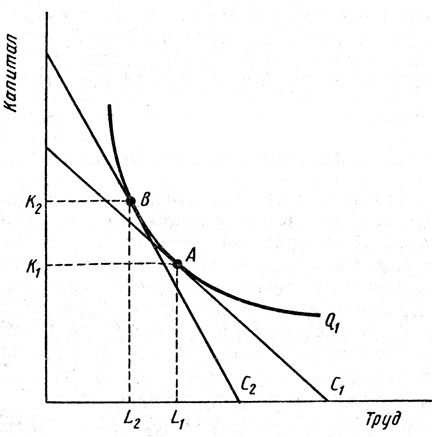
Рис. 7.3. Замена вводимого фактора, когда его цена меняется

В нашем анализе технологии производства мы показали, что предельная норма технического замещения (MRTS) труда капиталом равняется угловому коэффициенту изокванты, взятому с обратным знаком, и равна соотношению предельных продуктов труда и капитала:

Выше мы отмечали, что изокоста имеет наклон ΔК/ΔL = - w/r. Из этого следует, что когда фирма минимизирует издержки производства при некотором объеме выпуска, выполняется следующее условие:

Перепишем его в другой форме:

Уравнение (7.5) показывает, что при минимальных издержках каждый дополнительный доллар затрат на производственные факторы добавляет одинаковое количество выпускаемой продукции. Предположим, например, что ставка зарплаты составляет 10 долл., а арендная плата за капитал - 2 долл. Если фирма использует производственные факторы так, что предельный продукт труда и предельный продукт капитала равны 10, ей будет выгоднее нанимать меньше рабочих и "арендовать" больше капитала, потому что капитал в 5 раз дешевле труда. Фирма может минимизировать свои издержки только тогда, когда затраты на производство дополнительной единицы продукции одни и те же независимо от того, какой дополнительный фактор производства используется.

Пример 7.3. Воздействие штрафов за сброс промышленных сточных вод на выбор факторов производства

Металлургические комбинаты часто строятся вблизи рек. Река представляет собой недорогое транспортное средство как для перевозки руд к месту производства, так и для вывоза готовой продукции с завода. Река также представляет собой дешевый способ ликвидации отходов производственного процесса (сточных промышленных вод). Например, металлургический комбинат перерабатывает сырье методом измельчения таконитных полезных руд в пыль. В данном случае железо извлекается с помощью магнитного поля и далее направляется в технологический процесс. Отходы обогатительного производства сбрасываются в реку. Фирма платит за это относительно невысокие штрафы, тогда как альтернативные способы очистки или утилизации сточных вод обходятся значительно дороже.

Поскольку отходы обогащения представляют собой нерастворимые частицы, которые могут нанести ущерб посевам и рыбным запасам, Агентство по охране окружающей среды сочло необходимым накладывать штраф за промышленные сбросы. Как должен отреагировать руководитель фирмы при введении штрафных санкций, чтобы минимизировать издержки производства?

Предположим, что до введения санкций фирма производит 2000 т металла в день, используя капитал в 2000 машино - ч и 10 000 галлонов воды, содержащей отходы производства, которые возвращаются обратно в реку. Руководитель фирмы считает, что 1 ч машинного времени стоит 40 долл., а сброс использованных промышленных вод в реку обходится в 10 долл. за галлон. (Общие издержки производства, следовательно, составляют 180 000 долл.: 80 000 на капитал и 100 000 на сточные воды.) Как отреагирует руководитель на введение штрафа в 10 долл. за галлон промышленных отходов, спущенных в реку?

Рис. 7.4 показывает результат, минимизирующий издержки. На вертикальной оси откладывается использование фирмой капитала в машино - часах, а на горизонтальной оси показывается объем промышленных сбросов воды в галлонах. Рассмотрим вначале, как осуществляется производство на фирме, когда штраф за вредные сбросы отсутствует. Точка А представляет такое сочетание капитала и объема промышленных вод, которое позволяет фирме производить 2000 т металла в день при минимальных издержках. Так как фирма минимизирует издержки, А лежит на изокосте ВС, которая соприкасается с изоквантой. Угловой коэффициент изокосты равен - 10 долл./ 40 долл. = - 0,25, так как единица капитальных затрат стоит в 4 раза дороже единицы объема промышленных вод.

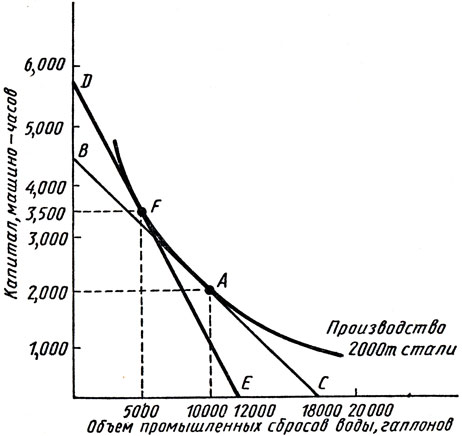
Рис. 7.4. График минимизации издержек производства в зависимости от объема

Когда сброс промышленных стоков облагается штрафом, стоимость использования промышленных вод возрастает с 10 до 20 долл. за галлон, так как за каждый галлон промышленных вод (который стоит 10 долл.) фирма должна платить дополнительно правительству еще 10 долл. Штраф за сброс промышленных вод увеличивает стоимость промышленных вод по отношению к капиталу. Чтобы производить тот же объем продукции при минимальных издержках, руководитель должен выбрать изокосту с угловым коэффициентом - 20 долл./ 40 долл. = - 0,5, которая соприкасается с изоквантой. На рис. 7.4 DE представляет собой соответствующую изокосту, а точка F - необходимое сочетание капитала и промышленных вод. Движение от А к F показывает, что при введении штрафных санкций за сброс промышленных вод применение альтернативных производственных технологий, которые делают упор на большем использовании капитала (3500 машино - ч) и меньшем - промышленных вод (5000 галлонов), выгоднее прежнего производственного процесса, который не предусматривал вторичного использования промышленных вод (общие издержки производства возросли до 240 000 долл.: 140 000 долл. на капитал, 50 000 долл. на промышленные воды и 50 000 долл. штрафа за сброс промышленных вод в реку).

Из этого решения мы можем сделать два вывода. Во - первых, чем легче замена факторов в производственном процессе, тем более эффективен штраф или другая санкция, чтобы сократить промышленные сбросы в реку. Во - вторых, чем выше норма замещения, тем легче фирме избежать штрафа. В нашем примере штраф мог бы достичь 100 000 долл., если бы фирма не внесла изменения в используемые факторы производства. Однако металлургический комбинат выплачивает только 50 000 долл. штрафа за счет передвижения производства от точки А к F.

Минимизация издержек при различных объемах производства

В предыдущем разделе мы видели, как фирма, минимизируя издержки, выбирает сочетание производственных факторов, чтобы достичь определенного объема производства. Теперь мы продолжим анализ, чтобы увидеть, как издержки фирмы зависят от объема выпуска продукции. Чтобы сделать это, определим для каждого объема производства количество факторов, которые минимизируют издержки, а затем подведем итоги.

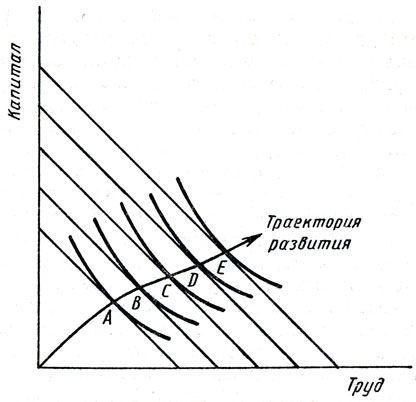
Рис. 7.5. Траектория развития производственной деятельности фирмы

Упражнение по минимизации издержек может быть выполнено для любого объема производства, рассматриваемого фирмой. На рис. 7.5 показан типичный результат данного анализа. Каждая точка - А, В, С, D и Е - представляет собой точку касания изокосты и изокванты фирмы. Кривая, идущая наверх и вправо от начала координат и прослеживающая точки соприкосновения, является траекторией расширения экономической деятельности. Эта линия включает все сочетания труда и капитала, которые выберет фирма, чтобы минимизировать издержки для каждого объема производства. Если использование обоих факторов производства увеличивается по мере роста выпуска продукции, кривая будет выглядеть примерно так, как на рис. 7.5. Траектория расширения экономической деятельности фирмы предоставляет информацию о валовых издержках на все переменные факторы производства при изменении объема выпуска продукции фирмы. Она подсказывает нам самые низкие валовые издержки на долговременном отрезке для каждого объема выпуска продукции.

дебетовые карты с кешбэком