§ 3. Многошаговые стохастические задачи

С постановкой детерминированной многошаговой задачи мы уже познакомились ранее в гл III. Теперь же будем считать, что не все параметры системы являются строго заданными величинами, а некоторые из них подвержены влиянию случая. Мы можем в той или иной степени воздействовать на этот многошаговый процесс, однако не в состоянии контролировать его полностью, так как ход его помимо управления зависит еще и от случая. Эта зависимость приводит к тому, что состояние S_j, в которое приходит система после завершения каждого шага, оказывается случайным, так же как и величина критерия (выигрыша) w_j на каждом шаге. Поэтому же оказывается случайным и суммарный выигрыш W независимо от того, каково было управление. Однако мы уже условились, как поступить в подобном случае: надо выбрать такое управление, при котором математическое ожидание выигрыша M (W) оказалось бы максимальным.

Будем считать, что критерий нашей задачи является аддитивным, и обозначим 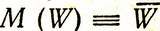Воспользовавшись тем, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий, напишем

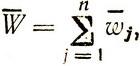
(4.10)

где 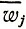- математическое ожидание выигрыша на j-м шаге.

Метод динамического программирования оказывается хорошо приспособленным для решения некоторых типов многошаговых стохастических задач, так как на каждом шаге переменные управления автоматически определяются как функции параметров состояния данного шага. Из-за этого часто многошаговые стохастические задачи прямо называют стохастическими задачами динамического программирования, рассматривая их как специальный вид задач динамического программирования. И действительно, казалось бы, при переходе от детерминированных задач к стохастическим задачам дело сводится к простой замене критерия. Однако это не так, поскольку различие между этими задачами заложено в самой структуре оптимального управления.

Для того чтобы показать, каким образом формулируется многошаговая стохастическая задача, рассмотрим следующую задачу о запасах [8].

Пусть на складе хранится запас некоторого товара в течение n периодов времени. Количество товара, отправляемого со склада, определяется спросом v_j на этот товар в j-й период. Спрос в каждый данный период считается случайной величиной с плотностью вероятности φ_j (v_j); предполагается, что для различных периодов эти случайные величины независимы. Пусть стоимость доставки с предприятия на склад Xj единиц заказанного на данный период j товара (заказ делается в начале каждого периода, а доставка производится до конца этого же периода) составляет c_jx_j. Допустим далее, что стоимость хранения запаса k_jy_j пропорциональна количеству товара y_j≥0 в конце j-го периода и за отсутствие на складе товаров при наличии спроса в j-й период начисляется штраф π_j, S_j, где S_j - число отказов к концу j-го периода. Требуется так спланировать поступление товара на склад, чтобы свести к минимуму все расходы на транспортировку товара, на хранение и штраф за отсутствие товара.

Обозначим через y₀ начальный запас товаров, т. е. запас в начале первого периода. Запас к концу j-го периода со ставит

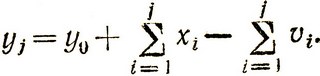
(4.11)

Очевидно, работа склада должна строиться таким образом, чтобы поддерживать y_j≥0. Однако это не всегда удается, и число отказов из-за отсутствия товаров на складе также к концу j-го периода оказывается равным

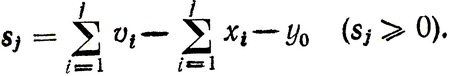
(4.12)

Наличие запаса и штрафа - взаимоисключающие моменты: если в течение какого-то периода y_j≥0, то S_j = 0, и наоборот, 1. е. если приходится платить за хранение в период j, то штрафа за отказ в этот период не будет.

Отобразим эту ситуацию посредством функции

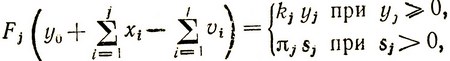
(4.13)

где y_j и S_j определяются выражениями (4.11) и (4.12).

Суммарные расходы склада за n периодов с учетом (4.13) составляют

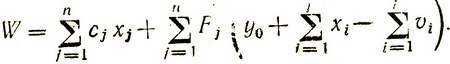
(4.14)

Так как спрос v_j является случайной величиной, то и все выражение (4.14) также является случайной величиной. Найдем математическое ожидание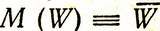

Как известно, плотность вероятности Φ (v₁, ..., v_n) появления некоторой определенной комбинации (множества) случайных статистически независимых величин равна произведению плотностей вероятности появления каждой из величин данного множества, т. е.

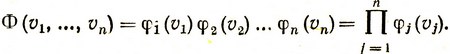
Математическое ожидание (среднее значение) расходов склада за n периодов есть

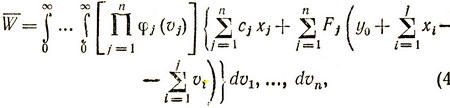
(4.15)

где интегрирование производится от 0 до ∞, так как все величины v_j положительные.

В процессе решения задачи мы должны выбрать значения x_j≥0, обеспечивающие получение минимального 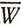. Однако мы не можем сделать это таким же образом, как в случае одношаговой задачи: сразу выбрать все n соответствующих чисел x_j≥0. Действительно, например, решение о том, какое количество товара следует заказывать в начале второго периода, зависит, во-первых, от того, сколько товара было завезено, и, во-вторых, от того, каков был спрос в течение этого периода, т. е. оптимальное значение x^*₂ является функцией y₂ - запаса в начале второго периода. Аналогично для любого кто периода имеем x^*_k = x^*_k (y_k). Такой подход к решению как раз соответствует подходу, который имеет место в динамическом программировании: управление на каждом шаге (периоде) выбирается исходя из результатов предыдущего шага. Именно поэтому и ранее высказывалось утверждение, что метод динамического программирования хорошо подходит для решения многошаговых стохастических задач. Рассмотрим теперь общую схему метода динамического программирования в применении к многошаговым стохастическим задачам [8] (далее для краткости эти задачи будем просто называть стохастическими задачами).

Как мы уже говорили, нас интересует не сам случайный выигрыш на любом j-м шаге, а его среднее значение (математическое ожидание). Поэтому в процессе решения задачи методом динамического программирования будет рассматриваться условный средний выигрыш на любом j-м шаге при заданном состоянии S_j-1 после (j-1)-го шага и определенном управлении на j-м шаге U_j, т. е.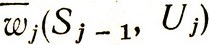

При этом мы будем предполагать, что как плотность вероятности появления случайного состояния S_j, так и условный средний выигрыш 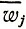не зависят от того, каким образом система пришла в состояние S_j-1, т. е. от того, как развивался процесс в прошлом. Процессы, обладающие таким свойством, называются марковскими случайными процессами, и для их описания в теории вероятностей разработан специальный математический аппарат. Нам надо показать, как для каждого из возможных случайных исходов любого шага определить уловное оптимальное управление на следующем шаге. При этом само оптимальное управление, U^* будет случайным (набором случайных величин) в том смысле, что при многократном повторении одного и того же процесса будет каждый раз выбираться иное управление в зависимости от того, как развернется случайный процесс.

Решение задачи в этом случае будет состоять в выработке для каждого шага такого управления, которое следует применять при любом случайном исходе предыдущего шага. Таким образом, в стохастической задаче оптимальное управление выбирается в ходе самого процесса в зависимости от случайно сложившейся ситуации. В таких условия^ можно говорить об управлении с "обратной связью", когда фактическое состояние системы влияет на вырабатываемое управление. В отличие от детерминированной задачи, где из возможных условных оптимальных управлений выбиралось только одно, в стохастической задаче в принципе каждое из условных оптимальных управлений может оказаться осуществляемым в сложившейся ситуации, т. е. когда ход случайного процесса приведет систему в такое состояние, что наиболее выгодно будет использовать данное управление.

Процесс решения как всегда разворачивается в обратном направлении начиная с последнего n-го шага. Для каждого возможного состояния системы S_n-1 после (n-1)-го шага ищем управление U_n^*(S_n-1), которое обращает в максимум средний условный выигрыш на n-м шаге:

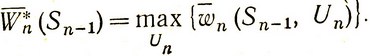
(4.16)

В рассмотренном выше примере максимальный выигрыш (4.15) состоял в получении минимальных затрат на хранение товара. Если считать затраты отрицательным выигрышем, то требование получения минимума затрат эквивалентно требованию получения максимального отрицательного выигрыша.

Далее переходим к оптимизации предпоследнего шага. Для некоторого состояния S_n-2, получившегося после (n-2) шагов, найдем средний выигрыш на двух последних шагах 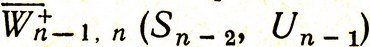при любом управлении U_n-1 и оптимальном управлении U^*_n (S_n-1), которое уже известно. При заданном S_n-2 и любом управлении U_n-1 состояние S_n-1 окажется случайным, однако по условию задачи для этого состояния известно распределение (плотность) вероятности¹, которая, вообще говоря, зависит от S_n-2 и U_n-1.

¹ (Здесь и далее употребляется термин "распределение вероятности", поскольку в динамическом программировании удобнее иметь дело с дискретными величинами. Понятия "распределение вероятности" и "плотность вероятности" эквивалентны по значению, однако первое из них мы относим к дискретным случайным величинам, а второе - к непрерывным.)

Максимальный средний условный выигрыш на n-м шаге 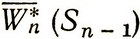определяется случайным состоянием S_n-1, распределение вероятности которого нам известно для заданного состояния S_n-2 и управления U_n-1. Усредним 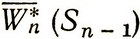с учетом распределения вероятности S_n-1 и получим дважды усредненный максимальный условный выигрыш, зависящий уже не от S_n-1, а от S_n-2 и U_n-1. Обозначим этот выигрыш

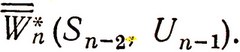
Средний выигрыш на двух последних шагах получим, прибавив к 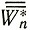средний условный выигрыш на (n-1)-м шаге при управлении U_n-1 на этом шаге:

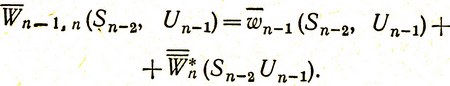
(4.17)

Эта величина обращается в максимум при условном оптимальном управлении U_n-1^* (S_n-2):

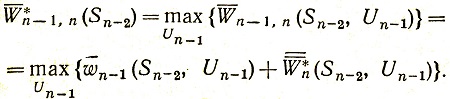
(4.18)

Выражение (4.18) определяет средний условный максимальный выигрыш на двух последних шагах. Подобным же образом оптимизируется любой j-й шаг. Порядок рассуждений при этом следующий.

Так как для каждого S_j (исхода j-го шага) уже известен условный максимальный средний выигрыш на всех последующих шагах 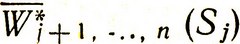, а состояние S_j случайное и его распределение вероятностей зависит от S_j-1 и U_j, то величину 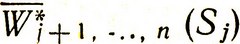следует усреднить с учетом этого распределения вероятностей, получив дважды усредненный выигрыш

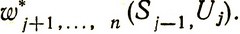
К этому выигрышу надо добавить средний выигрыш на j-м шаге при любом управлении 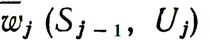. Условное оптимальное управление на j-м шаге U^*_j (S_j-1) выбирается таким, чтобы обратить в максимум величину

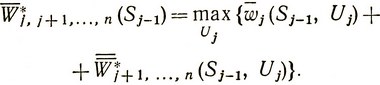
(4.19)

Последовательно применяя выражение (4.19), мы можем оптимизировать, таким образом, все шаги до второго включительно. Первый шаг оптимизируется по-разному в зависимости от того, каким образом задано исходное состояние S₀. Если S₀ случайно, как и все другие состояния, то оптимизация его производится точно так же, как и всех последующих шагов. Поскольку же S₀ обычно не является случайным, то по нему не нужно производить усреднение. Оптимальное управление U^*₁ при этом будет также вполне определенным и средний выигрыш составит:

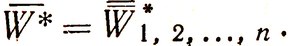
На этом заканчивается процесс решения задачи, так как уже найдено оптимальное управление

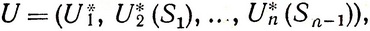
составленное из случайных оптимальных управлений на всех шагах кроме, может быть, первого.

В отличие от решения детерминированной задачи динамического программирования при решении стохастической задачи проходить последовательность шагов дважды (в прямом и обратном направлении) не нужно, так как все равно каждый раз, сколько бы раз мы этого ни делали, промежуточные состояния системы будут получаться различными и соответственно различным должно быть оптимальное управление. Важно то, что мы знаем, каково должно быть это управление для всех возможных состояний S_j. Поэтому применять управление (4.20) надо следующим образом: на первом шаге применить управление U^*₁ и ждать результатов этого шага; в зависимости от состояния системы S₁ после первого шага выбрать оптимальное управление U^*₁ (S₁) и ждать результата второго шага и т. д. до последнего шага. Управление такого вида можно назвать управлением с обратной связью, когда в ходе процесса в зависимости от его конкретного протекания выбирается управление, оптимизирующее окончательный результат. Именно в этом заложено глубокое различие между детерминированными и стохастическими задачами, о которых говорилось в начале настоящего параграфа.

Несмотря на то что как будто бы решать многошаговые стохастические задачи методом динамического программирования проще, чем детерминированные (не надо проходить дважды последовательность шагов), на самом деле не следует думать, что динамическое программирование может быть использовано для решения любых многошаговых стохастических задач. Да и сам процесс решения таких задач является значительно более трудоемким по сравнению с соответствующими детерминированными задачами.

В заключение покажем, как решается сформулированная ранее многошаговая задача о запасах (в предположении дискретности переменных). Пусть нам надо оптимизировать работу склада в течение квартала (трех месяцев). В соответствии со сказанным выше это означает, что мы должны так спланировать величины заказов x₁, x₂ и x₃ в начале каждого месяца, чтобы обеспечить получение минимальных полных затрат за квартал. Будем считать, что коэффициенты k_j и π_j - известные постоянные положительные числа, c_j<π_j и из предыдущего опыта нам известны вероятности p_kj дискретных значений спроса v_kj в каждом месяце, полученные, например, путем анализа вариационного ряда, содержащего l членов (k = 1, 2, ..., l).

Состояние системы определяется имеющимся на складе запасом y_j-1 к началу j-го периода (месяца). Затраты склада на транспортировку, хранение и штрафы в последнем третьем периоде, очевидно, составят

Здесь мы включили в функцию цели W три члена, однако следует помнить, что в конкретных примерах два последних члена никогда не должны встречаться вместе так же, как это было в задаче, рассмотренной в § 2.

Заменим v₃ его математическим ожиданием и оптимизируем результат последнего периода:

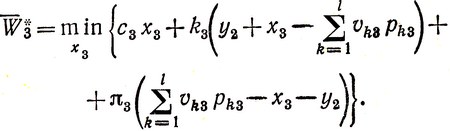
(4.21)

Очевидно, условное оптимальное управление есть

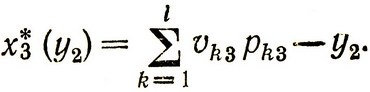
Далее переходим к оптимизации второго периода. Для этого записываем состояние системы y₂ в виде

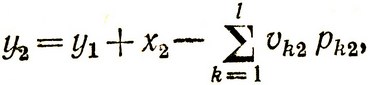
подставляем это выражение в (4.21), что дает нам дважды усредненный выигрыш 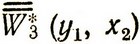, и затем получаем усредненные оптимальные затраты на втором и третьем периодах:

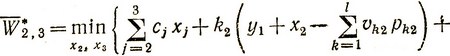
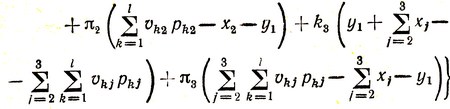
(4.22)

Условное оптимальное управление, которое следует применить, есть

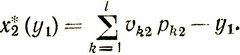
Аналогично записываются полные оптимальные средние затраты в течение всего квартала:

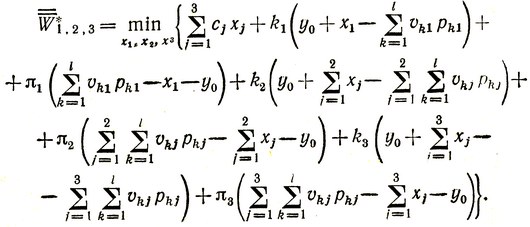
и оптимальное управление в первом месяце:

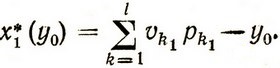
Поскольку величина заказа не может быть отрицательной, то следует считать, что x_j^* = 0, если соответствующая разность

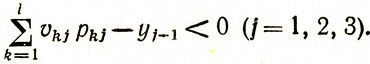
Таким образом, из решения этой задачи следует естественный вывод: всегда делать заказы такого размера, чтобы они равнялись разности между ожидаемым средним спросом в данном периоде и запасом, оставшимся от предыдущего периода.