
§ 2. Одношаговые стохастические задачи
Начнем рассмотрение стохастических одношаговых задач с простого примера, показывающего, как меняется задача линейного программирования, если считать, что некоторые ее параметры являются случайными величинами [8].
Рассмотрим транспортную задачу. Пусть однородный товар размещен на m складах и допустимое количество товара на i-м складе есть ai. Товар следует транспортировать в n магазинов, однако спрос в каждом магазине заранее точно не известен. Из предыдущего опыта торговли известно только, что потребности этих магазинов следует считать непрерывными случайными величинами с плотностью вероятности φj (vj), где j - номер магазина и vj - потребность этого магазина. Предполагается, что vj - независимые случайные величины, т. е. магазины расположены таким образом, что спрос в каждом из них не влияет на спрос в других магазинах.
Обозначим через cij стоимость перевозки единицы товара со склада i в магазин j. Полную стоимость перевозки будем считать пропорциональной количеству перевозимого товара xij.
Пусть yj - количество товара, поступившего в j-й магазин. Если это количество меньше спроса (yj<vj), то магазин не получит той выручки, которую мог бы получить (не говоря уже о потерях населения от неудовлетворенного спроса). Допустим, что получающиеся в этом случае потери описываются функцией πj (vj - yj), где πj - постоянная величина, равная
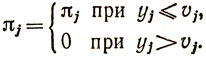
Если yj>vj, то магазин также терпит убыток, например, из-за того, что необходимо отправлять товар обратно на склад или продавать его по сниженной цене. Пусть получающийся в этом случае убыток описывается функцией kj (yj - vj), где kj - также постоянная величина, равная
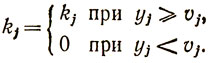
В этих условиях требуется определить наивыгоднейшее количества товара yj, поставляемого каждому магазину, при котором сводятся к минимуму транспортные расходы и возможные убытки от избытка или недостатка товаров при наличии случайного спроса.
Средние ожидаемые потери из-за нехватки товаров в j-м магазине, определяемые математическим ожиданием M1j случайной величины πj (vj - yj), есть
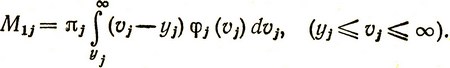
(4.3)
Аналогично средние ожидаемые потери, вызванные избытком товаров в j-м магазине, записываются в виде
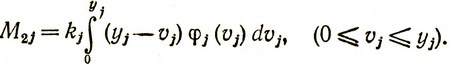
(4.4)
Прежде чем окончательно сформулировать задачу, удобно представить выражения (4.3) и (4.4) иначе. Используя тождественные преобразования, перепишем (4.3) в виде
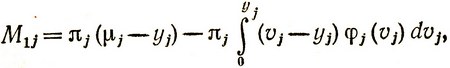
(4.5)
где 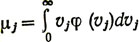 - ожидаемый спрос в j-м магазине (все vj≥0).
- ожидаемый спрос в j-м магазине (все vj≥0).
Пределы интегрирования в (4.5) предполагают изменение переменной vj в интервале 0≤vj<yj, где vj<yj, но именно в этом интервале по условию πj = 0. Значит, весь второй член в (4.5) также равен нулю, мы имеем:
M1j = πj(μj - yj).(4.5a)
Рассуждая точно так же, нетрудно показать, что
M2j = kj(yj - μj).(4.6)
Как в случае недостатка товара, так и в случае его избытка j-м магазине потери определяются разностью между действительным количеством товара yj и математическим ожиданием спроса на товар μj в данном магазине.
Полные затраты, включая транспортные расходы и ожидаемые потери из-за недостатка или избытка товаров по всем магазинам, согласно (4.5а) и (4,6) составляют
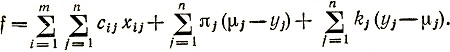
(4.7)
Вследствие условий, которым подчиняются величины πj и kj, можно сказать, что два последних члена в (4.7) никогда не должны встречаться вместе, поскольку недостача и избыток товара не могут возникнуть одновременно.
Сформулируем задачу окончательно следующим образом: Ври ограничениях
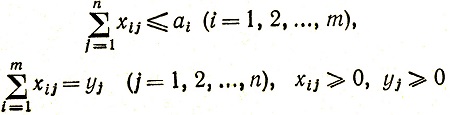
(4.8)
найти
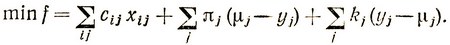
Отметим, что обратный переход от стохастической задачи (4.8) к соответствующей линейной транспортной задаче с постоянными параметрами легко осуществляется. Если положить yj = μj ≡ bj (при условии, что 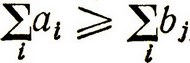 ), то мы сразу приходим к задаче:
), то мы сразу приходим к задаче:
при ограничениях
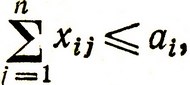
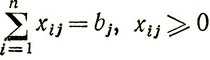
найти
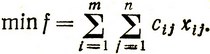
В этой задаче два ограничения, как и в задаче (4.8), Однако в задаче (4.8) от второго ограничения можно избавиться, исключив yj из функции цели. Оказывается, что всегда при переходе к стохастической задаче можно избавиться от тех ограничений детерминированной задачи, коэффициенты в которых являются случайными величинами. При этом появляется добавка в функции цели, которая учитывает убытки, появляющиеся при нехватке или излишках соответствующих ресурсов.
Все величины μj в (4.7), (4.8) получаются путем усреднения спроса vj с помощью соответствующих функций φj (vj). Фактически даже не решая задачи, можно сказать, что минимум полных затрат получится в том случае, если будет обеспечено равенство μj = yj для всех j магазинов.
В качестве примера рассмотрим случай, когда спрос подчиняется закону распределения:
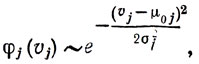
где, как известно, значение μ0j определяет положение максимума кривой распределения и σj характеризует ширину этой кривой. В этом случае величина
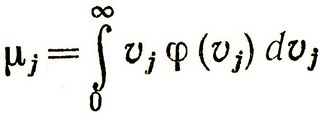
легко вычисляется и в результате мы получаем:
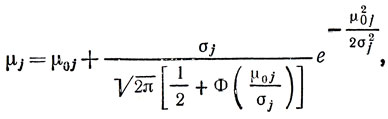
где 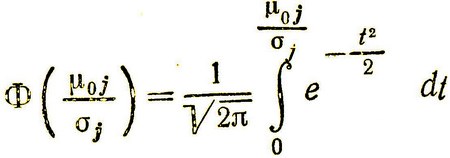 - функция Лапласа.
- функция Лапласа.
Таким образом, средний ожидаемый спрос μj отличается от μ0j, причем тем больше, чем меньше отношение 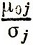 . В пределе
. В пределе 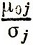 →,0 мы получаем
→,0 мы получаем 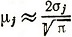 . Однако уже при
. Однако уже при 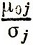 >4÷5 отличие μj от μ0j становится пренебрежимо малым.
>4÷5 отличие μj от μ0j становится пренебрежимо малым.
|
ПОИСК:
|
© ECONOMICS-LIB.RU, 2001-2022
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'
При использовании материалов сайта активная ссылка обязательна:
http://economics-lib.ru/ 'Библиотека по истории экономики'