Приложение

Принятие решений - один из элементов управления. Поэтому читателям книги было бы полезно познакомиться с некоторыми аспектами современной теории управления. Учитывая, что для этого нужна более основательная математическая подготовка, чем для чтения всех других разделов книги, рассмотрение проблем теории управления вынесено в приложение.

Общие сведения. Всякая система, которая изменяется с течением времени, обычно называется динамической системой. Пусть динамическая система в каждый момент времени характеризуется вектором состояния x=(x₁, x₂, ..., x_n). Например, для движущегося автомобиля эти величины могут означать координаты автомобиля, его скорость, направление движения, количество бензина в баке и т. п. Ради простоты в данный момент будем считать время меняющимся дискретно и моменты времени, когда наблюдается эта система, занумерованными так, что t₀<t₁<t₂<...<t_N<...

Предполагается, что вектор состояния x(t_k) полностью характеризует систему в момент t_k, описывает именно те характеристики Системы, которые для нас существенны (например, вектор состояния может не определять цвет автомобиля, если нас интересует только закон его движения). В каждый момент времени t_i известны множества V_i возможных управлений v_i, с помощью которых система переводится из одного состояния в другое. Вектор состояния системы в момент t_k+1 однозначно определяется всеми предыдущими состояниями и управлениями, применявшимися ранее, иными словами

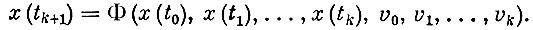
Для большей наглядности обратимся к геометрической интерпретации вышесказанного. Вектор состояния в каждый момент можно изобразить точкой n-мерного пространства, которое в теории динамических систем обычно называют фазовым пространством. Последовательность этих векторов, характеризующая движение системы, изображается последовательностью точек фазового пространства, носящей название траектории системы. Если время считать дискретным, то и траектория дискретна (рис. I б); при непрерывности времени траектория тоже непрерывна (рис. I а). Начальной точкой траектории служит x(t₀), и эта траектория конечна, т. е. имеет конечную точку x(t_N), если последний момент времени, в который рассматривается система, равен tN. Как правило, существует множество траекторий, переводящих систему из состояния x(t₀) в состояние x(t_N).

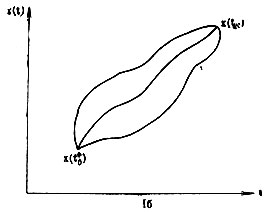
Рис. I a

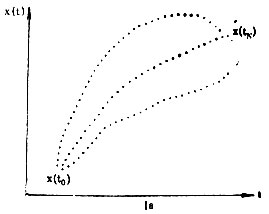
Рис. I б

Так как управление обычно экстремально - имеется цель перевести систему из одного состояния в другое за кратчайшее время, или с наименьшими затратами, или так, чтобы получить наибольший возможный доход и т. п., то естественно считать, что целью управления является отыскание такой траектории (и таких управлений в каждый момент времени), на которой заданная числовая характеристика качества траектории достигает экстремума (максимума или минимума). Будем предполагать, следовательно, что каждой из траекторий по некоторому правилу сопоставляется число (или, как говорят математики, на множестве траекторий задан функционал). Отметим, что правильная постановка задачи управления предполагает наличие только одного функционала. Причина в том, что если взять два произвольных функционала, то может не существовать такой траектории, на которой они оба достигнут экстремума. Имеет смысл искать экстремум только одного функционала при заданных ограничениях на другой (или другие).

Как связана теория управления с изучавшимися в книге вопросами принятия решений в различных экономических задачах? Дело в том, что экономику и отдельные ее подразделения можно рассматривать как динамические системы, которые в каждый момент времени описываются определенным вектором состояния. Компоненты вектора характеризуют различные технологические возможности, запасы сырья, ресурсы рабочей силы и др. Принятие решения означает перевод экономики из одного состояния в другое. В зависимости от потребностей общества та или иная траектория экономической системы является наиболее предпочтительной. Ее и следует определить. Налицо задача управления. Она характеризуется колоссальной размерностью векторов состояний, сложностью функций Ф, управлений и функционалов. Пока не имеется методов, позволяющих решить задачу управления во всей ее общности. Тем не менее экономистам полезно познакомиться с некоторыми основными принципами исследования задач управления, чтобы иметь и это оружие в арсенале средств анализа и решения экономических задач.

Вариационное исчисление. Рассмотрим такую экономическую задачу. В момент времени t функция x(t) характеризует величину выпуска продукции фирмы. Известно, что чистый доход фирмы в единицу времени зависит от величины выпуска (чем больше выпуск, тем больше затраты), скорости изменения этой величины (чем быстрее меняется величина выпуска, тем с большими переналадками это связано и, естественно, ведет к большим материальным затратам и затратам времени). Иначе говоря, чистый доход определяется функцией u(x(t), x′(t), t). Деятельность фирмы изучается в течение промежутка времени [0, T].

Заданы также величина выпуска в начальный момент x(0)=x₀ и желательная величина выпуска в конечный момент x(T)=x_T. При таких условиях требуется найти величину выпуска x(t) в каждый момент времени, причем так, чтобы суммарный доход за весь промежуток времени был наибольшим, т. е. требуется найти максимум функционала

(1)

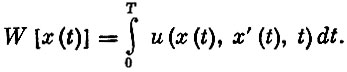
Множество дифференцируемых функций, заданных на [0, Т) и удовлетворяющих условиям x(0)=x₀ и x(T)=x_T, образует множество возможных траекторий. (В нашей задаче оно совпадает с множеством возможных управлений.) Та траектория, на которой функционал достигает экстремума, называется экстремалью. Вопросами поиска экстремалей для функционалов различного вида занимается вариационное исчисление, один из типичных подходов которого мы обсудим.

На рис. II изображено множество траекторий, соединяющих заданные начальное и конечное состояния. Попытаемся указать свойство, которое характеризовало бы экстремаль в целом. Пусть функция 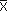(t) является экстремалью функционала (1). Если сравнить значение функционала на экстремали со значением его на любой из возможных траекторий, то из определения экстремали следует неравенство

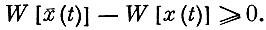
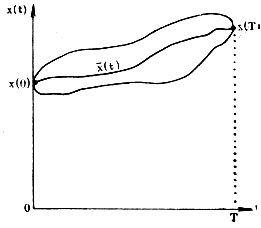
Рис. II

Выясним, как меняется значение функционала при переходе от экстремальной траектории к другой, достаточно близкой. Прежде всего заметим, что эта близкая траектория может быть получена путем малой "деформации" экстремали, как говорят, с помощью варьирования. Иными словами, всякую соседнюю с экстремалью траекторию можно описать функцией 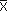(t)+δx(t), где δx(t) - произвольная дифференцируемая функция, принимающая малые значения, малы и значения (δx(t))′, а также выполняются граничные условия

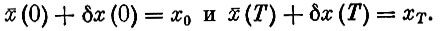
Из этих условий сразу следует, что δx(0)=δx(T)=0, т. е. при варьировании экстремали начальная и конечная точки остаются неподвижными.

Приращение функционала ΔW при переходе от экстремали к соседней траектории определяется равенством

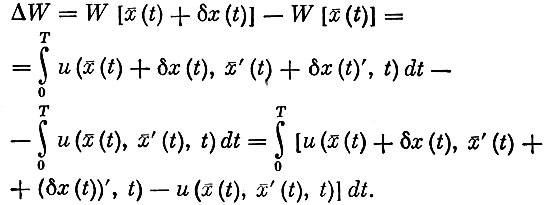
Пользуясь формулой Тейлора, разложим подынтегральное выражение, выделяя линейную часть разложения.

Имеем

(2)

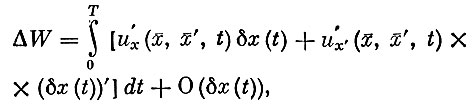
где О (δx(t)) - члены высшего порядка малости по сравнению с δx(t) и [δx(t)]

Так как ΔW≤0. отсюда с необходимостью следует, что линейная часть разложения должна равняться нулю. В противном случае перемена знака у произвольной функции δx(t) привела бы к перемене знака величины ΔW. (Это объясняется тем, что знак правой части (2) определялся бы знаком первого слагаемого, большего по величине, чем все остальные.) Поскольку перемены знака ΔW быть не может, справедливо равенство

(3)

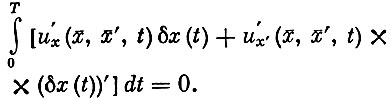
Именно равенство (3) и является необходимым условием, характеризующим экстремаль "в целом" - 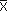(t) должна обязательно удовлетворять уравнению (3).

Покажем теперь, как преобразовать уравнение (3) для того, чтобы им удобнее было пользоваться.

Интегрируя по частям второе слагаемое в (3) и используя граничные условия δx(0)=0 и δx(T)=0, получаем

(4)

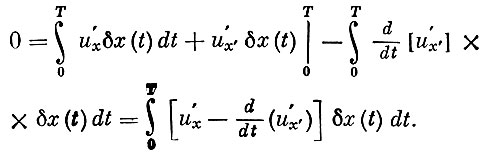
В силу произвольности функции δx(t) последний интеграл может равняться нулю только в том случае, когда выражение в квадратных скобках равно нулю. (Предполагается, что выражение в квадратных скобках и функция δx(t) непрерывны,)

Следовательно,

(5)

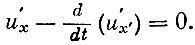
Полученное дифференциальное уравнение второго порядка носит название уравнения Эйлера. Решая это уравнение с заданными граничными условиями x(0)=x₀ и x(T)=x_T, можно найти экстремаль.

В качестве примера использования этого уравнения вернемся к рассматриваемой задаче, сделав ряд конкретных предположений. Будем считать, что u(x, x′, t)=ax-b(x′)² (доход в единицу времени складывается из дохода, обусловленного выпуском x(t), и затрат, связанных с изменением величины выпуска); x(0) и x(T) заданы. Окончательно приходим к следующей задаче: найти максимум функционала

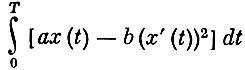
при граничных условиях x(0)=x₀ и x(T)=x₁. Составляем уравнение Эйлера для этого функционала

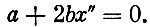
Решение уравнения дает

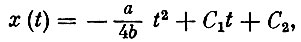
где C₁ и C₂ - произвольные постоянные, которые находятся из граничных условий, т. е. экстремаль представляет собой параболу.

Динамическое программирование. В § 1 гл. III рассматривался метод динамического программирования, весьма эффективный при изучении многошаговых процессов принятия решений. Тот же метод оказывается полезным и при решении непрерывных задач управления. Чтобы показать это, сначала опишем концепцию в целом, а потом проиллюстрируем ее на примере.

Применяя методы вариационного исчисления, пытаются сразу охарактеризовать искомый объект путем построения дифференциального уравнения, решением которого и является искомая экстремаль. Между тем это не единственный путь. Представляется возможным находить экстремальную траекторию не всю сразу, а по частям, пусть даже очень маленьким. Грубо говоря, ситуация подобна следующей. Если нам нужно дать указание, как пройти из одного пункта в другой, то либо следует сразу описать всю дорогу, либо после каждого шага сообщать, куда следует сделать очередной шаг. В этом случае человек будет полностью знать дорогу, когда дойдет до конечного пункта. Так вот, первый способ аналогичен методу вариационного исчисления, второй же - методу динамического программирования.

Подобная двойственность описания одного и того же объекта обусловлена тем, что всякую гладкую кривую можно трактовать либо как геометрическое место точек, удовлетворяющих некоторому уравнению, либо как огибающую семейства касательных к этой кривой.

Итак, задачу поиска непрерывной экстремали можно рассматривать как непрерывный процесс принятия решений - в каждой ее точке мы должны уметь находить куда передвинуться, чтобы попасть в следующую точку. Разумеется, это всего лишь математическая абстракция, так как физически неосуществимо принятие решений во всех точках кривой - их слишком много. При решении конкретных задач непрерывная кривая аппроксимируется ломаной или заменяется дискретным множеством точек. Рассмотрим этот метод на примере уже известной нам задачи, несколько видоизменив ее.

Будем считать, что доход фирмы в единицу времени зависит от объема выпуска продукции x(t), от наличного основного капитала фирмы K(t) и времени t, т. е. определяется функцией u(K(t), x(t), t). Запас капитала связан с принимаемым решением - величиной выпуска - таким соотношением

(6)

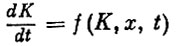
(скорость накопления в каждый момент есть функция от имеющегося основного капитала, величины выпуска и момента времени). Известен также начальный размер основного капитала K(0)=C. При этих условиях требуется, так же как и раньше, найти объем выпуска продукции x(t), который доставлял бы максимум функционалу

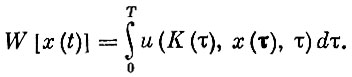
Основное отличие этой задачи от той, что была рассмотрена выше, состоит в наличии ограничения (6), обусловливающего тот факт, что принимаемое решение имеет двойной эффект - немедленный вклад в суммарный доход и воздействие на запас капитала и доход в последующие моменты времени. На вдаваясь в математические тонкости, отметим, что это ограничение не дает возможности непосредственно использовать уравнение Эйлера для нашей задачи. Нужно сказать, что и вообще использование для нее классических методов вариационного исчисления весьма затруднено. Методы же динамического программирования позволяют преодолеть возникающие трудности. Это тем более ценно потому, что в реальных задачах, как правило, приходится сталкиваться именно с экстремальными задачами с ограничениями.

Итак, мы должны уметь в каждый момент времени t наилучшим образом выбирать функцию x(t). Сопоставим этой задаче ее дискретную аппроксимацию. Будем искать

(7)

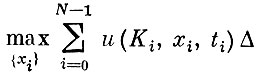
при условиях

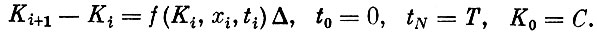
Здесь приняты обозначения K_i= K(t_i) и x_i=x(t_i), а t₀, t₁, ..., t_N - моменты времени из промежутка t, отстоящие друг от друга на величину А.) Тем самым, вместо того чтобы искать функцию x(t), заданную на промежутке [0, Т], мы будем только выбирать значения ее в фиксированных заранее точках t₀, t₁, ..., t_N.

"Погрузим" нашу задачу в семейство таких однотипных задач: найти максимум функционала

(8)

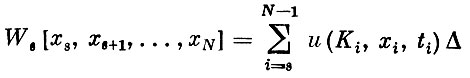
при условиях

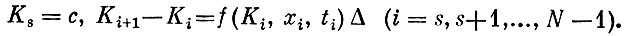
Понятно, что максимум каждого такого функционала зависит от величин s и с. Обозначим его через Ф₈(c), т. е.

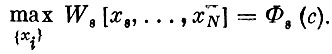
На основании принципа оптимальности (см. выше) сразу же можно прийти к следующим рекуррентным соотношениям:

(9)

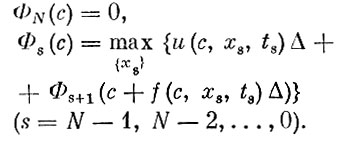
Вычисляя последовательно функции Ф₈(с) и запоминая соответствующие оптимальные стратегии, можно найти численное решение поставленной задачи - величина Ф₀(С) представляет собой максимальное значение функционала задачи (7), величины же x_i, на которых достигаются максимумы в соотношениях (9), определяют оптимальные объемы выпуска продукции в моменты t_i. Важно заметить, что если величины x_s подчинены каким-либо дополнительным ограничениям, то максимум берется по допустимому множеству значений. В этом большое преимущество метода динамического программирования.

Принцип максимума Понтрягина. Начнем с геометрического пояснения этого принципа, разработанного советским математиком, академиком Л. С. Понтрягиным и его сотрудниками, а уже потом перейдем к соответствующему аналитическому аппарату. В качестве иллюстрации по-прежнему будем использовать задачу об определении объема выпуска продукции фирмы.

Для большей простоты предположим, что объем выпуска продукции непосредственно на приращении дохода не сказывается. Другими словами, будем считать, что функция u(K, x, t) на самом деле не зависит от x.

Состояние динамической системы - фирмы - в каждый момент вполне определяется ее наличным капиталом K. Цель управления - максимизация дохода - состоит в том, чтобы среди всех траекторий на плоскости (K, t), исходящих из данной точки (c, 0), найти ту, на которой достигает максимума функционал (1).

Для каждой точки (K, t) (0≤t≤T) рассмотрим задачу о том, как следует управлять фирмой, имеющей в момент t капитал К, чтобы обеспечить за время от t до Т максимум дохода. Величина этого максимального дохода, очевидно, зависит от начальной точки (K, t), так что на плоскости (K, t) при 0≤t≤T определена функция V^* (K, t).

Изобразим линии уровня этой функции (см. рис. III). Внешние нормали к линиям уровня этой функции обладают очень важным свойством: они указывают скорость накопления капитала, обеспечивающую наибольшее относительное приращение дохода (на единицу капиталовложений). Если, имея в момент t капитал K, мы установим объем выпуска продукции равный x, то фактически на плоскости (K, t) мы будем двигаться в направлении вектора z с компонентами (f(K, x, t), 1). Поэтому для обеспечения максимального приращения дохода мы должны выбирать объем выпуска продукции x так, чтобы проекция вектора z на внешнюю нормаль к линии уровня функции V^* в соответствующей точке была максимальна.

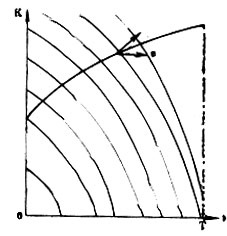
Рис. III

Такова идейная сторона принципа максимума. Аналитический аппарат мы проиллюстрируем на более общей задаче, не предполагая независимости функции u от x. Пусть

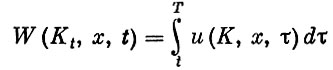
и

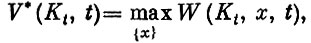
где максимум берется по всем допустимым управлениям x.

Понятно, что первая величина выражает доход, полученный фирмой за время от t до T, если в момент t запас капитала равняется K_t и выбрано управление x(t). Вторая же - доход, соответствующий оптимальному управлению 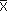(t).

Промежуток времени [t, Т] разобъем на две части - короткий промежуток Δ и остающийся [t+Δ, Т]. Тогда, применяя принцип оптимальности, можно получить такое соотношение

(10)

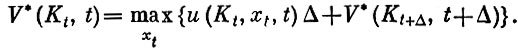
(максимальный доход, получаемый от момента t до T, если в момент t запас капитала K_t);

(доход за короткий промежуток Δ);

(максимальный доход, получаемый от момента t+Δ до T, если в момент t+Δ запас капитала K_t+Δ);

С другой стороны, если 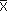t - оптимальный выпуск в момент е, то с точностью до бесконечно малых более высокого порядка, чем Δ,

(11)

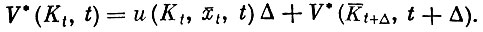
Предположим для простоты, что V^* дифференцируема. Тогда из (10) (с точностью до бесконечно малых высшего порядка) следует

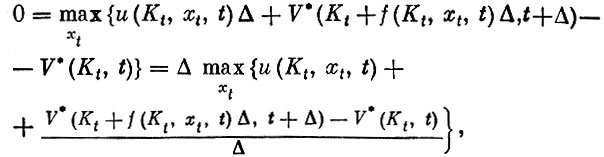
откуда следует, что

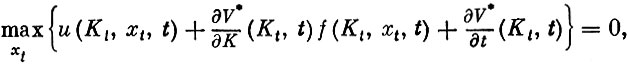
или, полагая

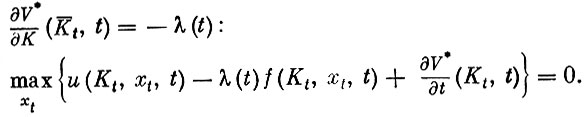
Точно так же из (11) можно получить равенство

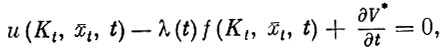
т. е.

(12)

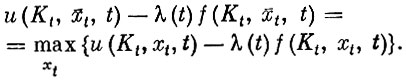
Наконец, дифференцируя соотношение (11) по K_t (принимая во внимание, что K_t+Δ=K_t+f(K_t, 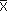_t, t) Δ) и устремляя Δ к нулю, получаем

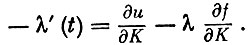
Величина - λ′ (t) характеризует скорость обесценивания единицы капитала в момент t.

Итак, можно сделать следующий вывод. Оптимальное управление X в каждый момент должно удовлетворять таким уравнениям:

(I)

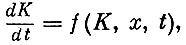
(II)

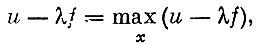
(III)

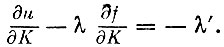
Американский экономист Дорфман, исследовавший данную задачу, придает этим уравнениям следующий экономический смысл:

(I) - характеризует темп роста капитала в каждый момент в зависимости от текущего состояния и принимаемого управления;

(II) - показывает, что очищенный доход, т. е. доход, из которого исключена маргинальная предельная оценка накапливаемого капитала, в каждый момент максимален на оптимальной траектории;

(III) - скорость обесценивания капитала при оптимальном управлении определяется маргинальной оценкой капитала для максимизации дохода. Чем выше эта оценка, тем медленнее происходит обесценивание.

Решение уравнений (I)-(III), составляющих аналитическое выражение принципа максимума, может быть осуществлено одним из многочисленных методов, разработанных в теории дифференциальных уравнений. Нередко оно оказывается более простым, чем решение исходной задачи другими методами.