3. Модели развития экономики

Рассмотрим модель развития экономики, разработанную английским экономистом Р. Харродом (сходные модели были предложены еще ранее советским экономистом Фельдманом). Несмотря на простоту - в модели учитывается всего только один ограниченный фактор - капитал - с ее помощью может быть проведено грубо приближенное исследование закономерностей роста экономики. В модели используются такие обозначения: y(t) - национальный доход; k(t) - капитал (производственные фонды),c(t) - объем потребления; s(t) - объем накопления; j(t) - инвестиции (капиталовложения).

Предполагается, что экономика функционирует так, что выполняются соотношения

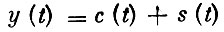
(национальный доход распределяется между накоплением и потреблением);

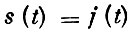
(накопления равны инвестициям);

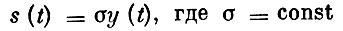
(накопления составляют постоянную долю национального дохода);

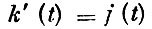
(темп роста капитала равен инвестициям);

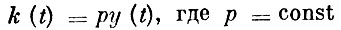
(отношение капитала к национальному доходу - величина постоянная - наблюденный эмпирический факт). Из уравнений, описывающих модель, сразу же следует

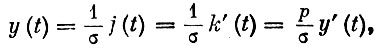
или

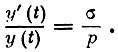
Следовательно, темп роста национального дохода равен σ/p и, значит, если предположить, что в начальный момент времени (при t=0) национальный доход равен y₀, то закон его изменения во времени имеет следующий вид:

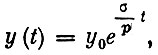
что зачастую неплохо согласуется с практикой.

Для описанной модели естественным образом возникают две задачи. Первая из них может быть названа задачей управления. В ней задан закон изменения национального дохода во времени в виде известной функции φ(t) и требуется так подобрать изменение параметра σ, чтобы функция y(t) в какой-то степени была близка к φ(t) (разумеется, управление должно быть выбрано так, чтобы не нарушались сделанные выше гипотезы). Вторая задача может быть охарактеризована как определение поведения модели при выбранном управлении. В этой задаче выбран параметр управления σ в допустимых для него пределах и требуется определить закон изменения национального дохода. Результаты решения таких задач, полученные, однако, для более точных моделей, представляют не только теоретический, но и практический интерес.

Перед тем как перейти к рассмотрению другой макроэкономической модели, укажем важную экономическую проблему. Для определения эффективности капиталовложений и для расчета цен необходимо знание такого параметра экономической системы, как норма эффективности капиталовложений. Подробное описание роли этого параметра будет дано в шестой главе, а здесь важно лишь заметить, что некоторую количественную оценку норматива эффективности и качественную характеристику его зависимости от других параметров системы можно получить в результате исследования макроэкономических моделей. Вот один из возможных вариантов такой оценки.

Будем рассматривать экономическую систему, в которой производится только один продукт. Частично он используется для потребления, частично же идет на увеличение основных и оборотных средств. Обозначим через P(t) количество чистой продукции (национальный доход), производимое в единицу времени. Наличные фонды в момент t составляют K(t), а ресурсы труда T(t). Предполагаем, что величина P(t), определяется значениями T и K, представляет функцию этих переменных

(5)

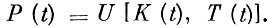
Эта функция U называется производственной функцией.

Здесь функция T(t) считается заданной. Она определяется динамикой численности рабочих и служащих в народном хозяйстве, а по существу - демографическими данными. Функция K(t), обозначающая фонды народного хозяйства в момент t, является искомой. Известно только ее начальное значение K(0).

Примем две довольно естественные гипотезы. Во-первых, будем считать, что производственная функция U уже включает в себя элемент оптимальности, т. е. она строится на основе наилучшего использования имеющихся объемов фондов и труда, обеспечивающего производство максимального количества продукта в единицу времени.

Во-вторых, считаем функцию U положительно однородной. Это значит, что если ресурсы труда и капитала увеличиваются в λ раз, то и продукции производится в λ раз больше, иначе говоря,

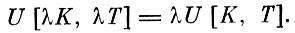
Относительно объема потребления V(t) естественно предполагать, что он определяется параметрами системы в данный момент, т. е. представляет заданную функцию их:

(6)

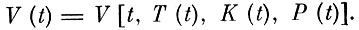
Используя соотношения (5) и (6), можно описать развитие экономики - скорость приращения фондов - таким дифференциальным уравнением:

(7)

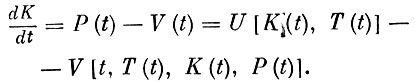
На первый взгляд кажется, что в уравнении (7) нет никаких параметров, по которым осуществляется оптимизация. Однако это не так. Оптимизация неявно произошла за счет принятия первой гипотезы о непрерывном оптимальном преобразовании фондов и применении производственной функции, соответствующей оптимальному выбору производственных способов. Можно сказать поэтому, что в модели осуществляется в некотором смысле дифференциальная оптимизация, т. е. в каждый момент времени мы выбираем ту стратегию, которая дает наибольший прирост фондов в этот момент, учитывая, однако, требования потребления, подлежащие удовлетворению.

Приступим теперь к определению нормы эффективности капиталовложений. Для народного хозяйства норма эффективности есть тот прирост чистой продукции, который дает в единицу времени целесообразно использованная дополнительная (предельная) единица капиталовложений. Если обозначить норму эффективности через η_э, то данное выше определение можно записать на языке математики так:

(8)

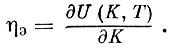
Выразим величину η_э через другие переменные и параметры модели. Сначала, однако, введем и в уравнение (7) и в равенство (8) новую неизвестную функцию - фондовооруженность S, которая представляет объем фондов, приходящийся на единицу труда

(9)

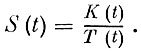
После этого (7) и (8) приобретают вид

(7′)

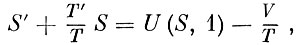
(8′)

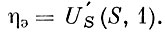
Кроме того, требуется ввести в рассмотрение темп роста национального дохода, т. е. величину 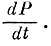Дифференцируя (5), получаем

(10)

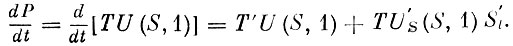
Отсюда, заменяя U′_s(S, 1) на η_э на основании (8′) и используя равенства (10) и (8′), решаем уравнение (7′) относительно η_э

(11)

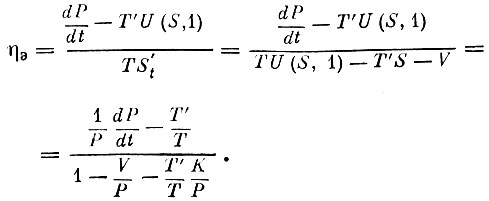
Величины, входящие в формулу (11), имеют ясный экономический смысл: в числителе - относительный темп роста народного дохода (1/P dP/dt), темп роста трудовых ресурсов (T′/T); в знаменателе - фондоемкость (K/P), доля потребления в народном доходе (V/P).

Из формулы (И), делая различные предположения относительно производственной функции и функции потребления, можно получить более простые выражения для η_э. В частности, для производственной функции вида

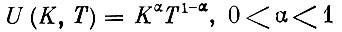
(это довольно часто используемый вид производственной функции, носящей название функции Кобба - Дугласа) норма эффективности капиталовложений выражается совсем простой формулой

(12)

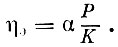
Все показатели, использованные для построения формул (5)-(12), имеют реальный экономический смысл и могут быть количественно определены из статистических данных, которые содержатся в статистических справочниках ЦСУ СССР. Вот, например, какими были эти показатели в 1965 г. (табл. 28).

Таблица 28

Норма эффективности капиталовложений, рассчитанная на основании этих данных по приведенным формулам, составляет величину порядка 22%. Если в модели учесть технический прогресс, период "созревания" фондов (лаг), физический и моральный износ действующих фондов (это немного усложняет модель, но не изменяет принципов ее построения), то норма эффективности понижается до 18-20%. Эта также высокая величина нормы соответствует тому положению, что народное хозяйство СССР использует свои капитальные вложения с относительно высокой эффективностью. Дальней лее совершенствование планирования народного хозяйства СССР, опирающееся на применение математико-экономических методов, позволит еще более поднять эффективность социалистического производства.