4. Общая задача линейного программирования

Выше были подробно рассмотрены частные задачи линейного программирования. Теперь настало время познакомиться с общей постановкой этой задачи. Построим математическую модель организации производства. В этом производстве участвуют m различных производственных факторов (ингредиентов) - рабочая сила, сырье, материалы, оборудование, конечные и промежуточные продукты и др. Производство использует S технологических способов, причем для каждого из них заданы объемы производимых ингредиентов, рассчитанные на реализацию этого способа с единичной интенсивностью, т. е. задан вектор a_h=(a_1k, a_2k, ..., a_mk), k=1, 2,..., S, в котором каждая из компонент a_ik указывает объем производства соответствующего (i-го) ингредиента, если она положительна, и объем его расходования, если она отрицательна (в способе k). Выбор плана означает указание интенсивностей использования различных технологических способов, т. е. план определяется вектором x=(x₁, x₂, ..., x_S) с неотрицательными компонентами.

Для каждого плана x легко подсчитать балансы по каждому из ингредиентов. Эти балансы являются компонентами вектора

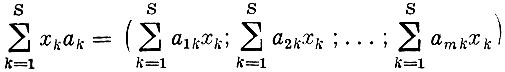
(положительная компонента - объем производства (выпуска) ингредиента, отрицательная компонента - объем затрат ингредиента).

Обычно на количества выпускаемых и затрачиваемых ингредиентов накладываются ограничения: производить нужно не меньше, чем требуется, а затрачивать не больше, чем имеется. Такие ограничения записываются в виде

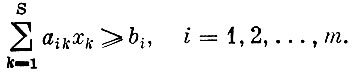
Если b_i≥0, то неравенство означает, что имеется потребность в ингредиенте в размере b_i; если b_i≤0, то неравенство означает, что имеется ресурс данного ингредиента в размере - b_i=|b_i|.

Далее предполагается, что использование каждого способа связано с расходом одного из перечисленных ингредиентов или особо выделенного ингредиента в количестве C_k при единичной интенсивности способа a_k. В качестве целевой функции принимается суммарный расход этого ингредиента в плане

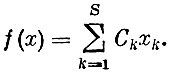
Теперь общая задача линейного программирования может быть представлена в математической форме. Для заданных чисел a_ik, C_k и b_i найти

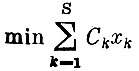
при условиях

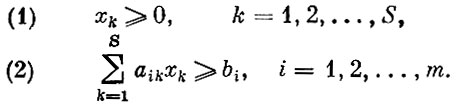
План, удовлетворяющий условиям (1) и (2), является допустимым, а если на нем, кроме того, достигается минимум целевой функции, то этот план оптимальный.

Итак, задача состоит в отыскании минимума линейной функции при линейных ограничениях, или, иначе говоря, минимума этой функции на выпуклом многограннике допустимых планов. Признак оптимальности плана формулируется в виде такой теоремы.

Для оптимальности допустимого плана х необходимо и достаточно существование вектора

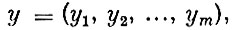
удовлетворяющего условиям

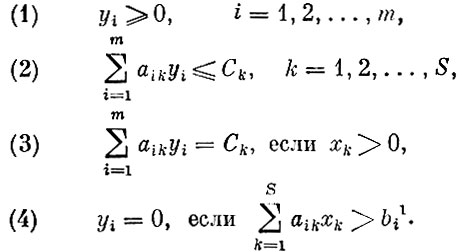
¹ (Доказательство теоремы. Пусть вектор х′=(х′₁, x′₂ . . ., х′_S) представляет собой какой-то допустимый план. Подсчитаем значение целевой функции для плана х′; используя условие (2) признака оптимальности, имеем 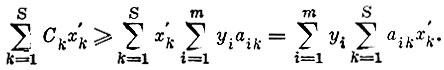Так как план допустим, справедливо неравенство 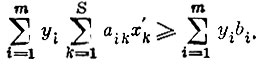Из условия допустимости плана х и условий (4) и (3) следует 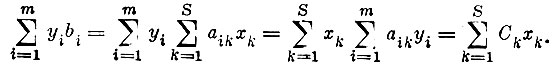Таким образом, 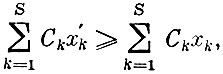т. е. план х оптимален, так как любому допустимому плану соответствует не меньшее значение целевой функции, чем плану х. Доказательство необходимости условия теоремы, т. е. наличия оценок, согласованных с планом, не приводим.)

Компоненты вектора y можно рассматривать как о. о оценки для всех видов ингредиентов. На "языке" этих оценок все условия теоремы имеют прозрачный экономический смысл: (1) оценка каждого ингредиента неотрицательна; (2) для каждого возможного способа получаемый эффект, который выражается алгебраической суммой оценок произведенных и затраченных ингредиентов, не превосходит C_k - расхода, связанного с применением способа; (3) в оптимальный план могут включаться только такие технологические способы, для которых суммарная алгебраическая оценка получаемой продукции равна расходу C_k; (4) ингредиенты, получаемые в оптимальном плане с избытком, имеют нулевые оценки.

Очень важно отметить, что вектор оценок y, соответствующий оптимальному плану, сам является решением двойственной задачи линейного программирования, которая формулируется следующим образом.

Для заданных чисел a_ik, b_i, C_k найти

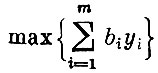
при условиях

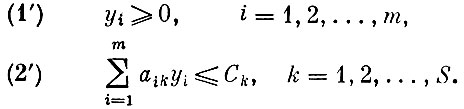
Читатель, внимательно ознакомившийся с объяснением того, как составлялась двойственная задача к задаче раскроя (см. выше), без труда сможет установить экономический смысл этих отношений.

Связь между прямой и двойственной задачами линейного программирования характеризуется тем, что если одна из них имеет решение, то разрешима и другая. При этом для оптимальных планов этих двух задач справедливо соотношение

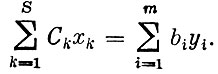
Это утверждение носит название теоремы двойственности.

Использование теоремы двойственности и связанного с ней признака оптимальности допустимого плана лежит в основе большинства эффективных методов решения задач линейного программирования. В § 2 был описан один из них - метод последовательного улучшения плана. Близко к нему примыкает симплекс-метод, разработанный американским математиком Дж. Данцигом. Приведем краткое описание этого метода.

В постановке задачи линейного программирования каждое неравенство

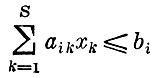
может быть заменено на равенство прибавлением к левой части вновь вводимой неотрицательной переменной

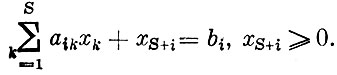
Полагая что n=S+m и C_S+i=0(i=1, 2, ..., m), Случаем возможность рассматривать задачу линейного программирования (благодаря увеличению числа переменных) в следующей канонической форме, найти

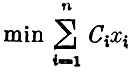
при условиях

(1)

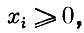
(2)

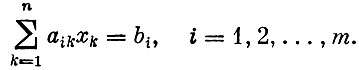
Предположим, что уже имеется допустимый план х, причем такой, что способы, используемые в нем, являются базисными векторами (такой план называется опорным)^*. Можно считать, что базис состоит из первых m векторов a₁, a₂, ..., a_m, так как этого всегда можно добиться изменением нумерации способов. Поскольку всякий вектор m-мерного пространства можно разложить по этому базису, найдем разложения всех векторов способов и вектора ограничений. Коэффициенты этих разложений объединены в табл. 3 (так называемая симплексная таблица).

^* (Мы говорим, что m векторов m-мерного векторного пространства образуют базис, если они линейно независимы, т. е. ни один из них не может быть выражен через другие. Тогда всякий вектор х пространства может быть единственным образом выражен через векторы базиса х=ξ_1a1+ξ_2a2+...+ξ_mam, где величины ξ_k - коэффициенты разложения.)

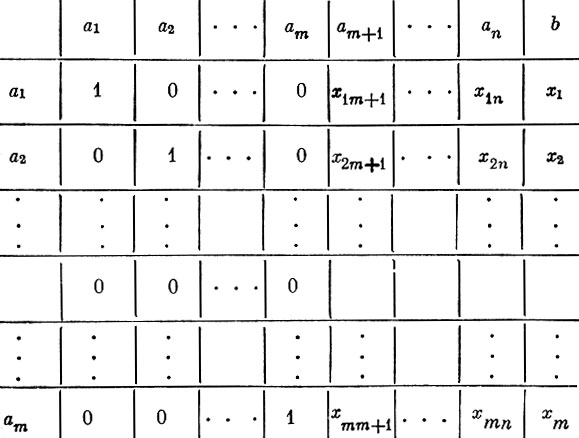
Таблица 3

В частности, для самих базисных векторов записаны их очевидные разложения типа

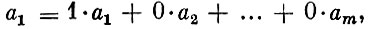
для небазисных векторов

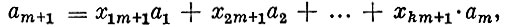
где x_km+1 - коэффициенты разложения. Наличие разложения b=х₁а₁+х₂а₂+ ... +х_ma_m для вектора b=(b₁, b₂, ..., b_m) с неотрицательными x_k вытекает из предположения, что план х допустимый.

Процедура симплекс-метода состоит из двух этапов.

1. Проверка плана на оптимальность.

2. Включение рентабельных способов и вытеснение из базиса нерентабельных способов.

Базисность допустимого плана означает, что любой способ, не используемый в этом плане, можно выразить через используемые способы. Пусть производственный способ a_S не был включен в план. Тогда его можно "синтезировать" из базисных способов, т. е. 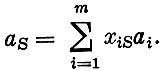Расход a_S для этого "синтетического" способа определяется равенством 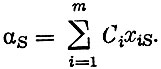Если "синтетический" способ дороже, чем способ a_S, то целесообразно заменить его способом a_S путем введения последнего в базис. Пусть способ a_S вводится в базис с интенсивностью θ. Для того чтобы не нарушались балансовые соотношения, нужно изменить интенсивность, с которой применяются остальные способы. Из написанного выше разложения a_S ясно, что интенсивность x_i, с которой применялся способ a_i, следует уменьшить на величину θx_iS. Так как интенсивности не могут быть отрицательными, нужно обеспечить выполнение неравенств

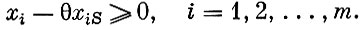
Отсюда следует, что 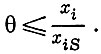Ясно, что наибольшее допустимое

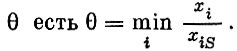
Допустим, что минимум тот достигается при 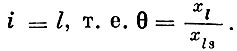Принимая такую интенсивность для вновь вводимого способа a_S, получим, что 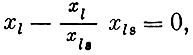т. е. способ a_l применяется с нулевой интенсивностью - выводится из базиса. Таким образом, построен новый, лучший план.

Приступим теперь к более формальному описанию симплекс-метода. Для каждого небазисного способа можно сравнить два числа

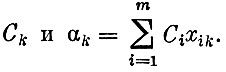
Из критерия оптимальности ясно, что план х оптимален тогда и только тогда, когда C_k≥α_k для всех k. Действительно, если для какого-нибудь k выполняется неравенство α_k>C_k, то план неоптимален и способ a_k целесообразно ввести в новый базис. Если таких k несколько, то естественно ввести один из них, например, тот, для которого разность α_k - C_k максимальна. Пусть он соответствует k=S.

Для того чтобы новый допустимый план был опорным, необходимо исключить один из использовавшихся способов, так как m+1 векторов в m-мерном пространстве всегда линейно зависимы и базиса не образуют. Подсчитаем величину 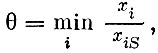где индекс i соответствует положительным компонентам плана. В силу предположения, сделанного выше, 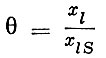Тогда исключить из базиса следует именно способ a_l и новому плану будет соответствовать базис a₁, a₂, ..., a_l-1, a_l+1, ..., a_m, a_S.

Теперь покажем, как перейти от плана x к лучшему допустимому плану x′. Раскладывая вектор ограничений по новому базису, имеем

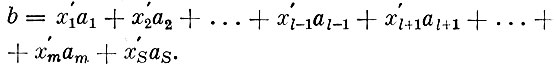
С другой стороны, используя имевшиеся ранее разложения векторов b и a_l, тот же вектор b можно представить в таком виде

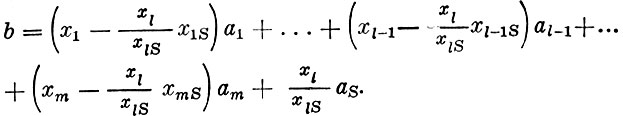
Отсюда следует, что новый план может быть вычислен по формулам

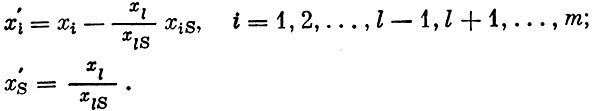
Важно отметить, что х′_i неотрицательны. Это ясно из выбора θ. Совершенно аналогичные формулы можно получить и для преобразования всех элементов симплексной таблицы (табл. 3)

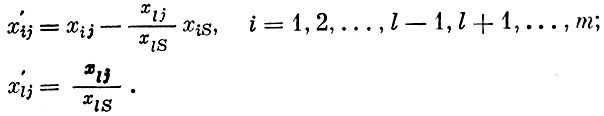
Отысканием нового плана и преобразованной таблицы завершается одна итерация симплекс-метода. Далее этапы проверки и улучшения повторяются снова. Доказано, что если оптимальное решение задачи существует, то оно будет найдено через конечное число шагов (за исключением редко встречающихся случаев вырождения, требующих некоторого изменения алгорифма)^*.

^* (Описание метода исходило из предположения, что допустимый план существует. Правильно поставленная задача действительно обычно имеет решение, однако трудности нередко возникают при отыскании допустимого опорного плана. В таких случаях используется метод искусственного базиса, связанный с введением в задачу дополнительных способов.)

В качестве иллюстрации применим симплекс-метод к решению конкретной задачи. Найти

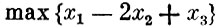
при условиях

Здесь

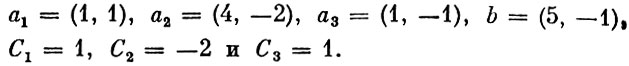
Эта задача отличается от рассматривавшейся задачи линейного программирования в канонической форме тем, что в ней требуется отыскать максимум, а не минимум. Понятно, что план я такой задачи оптимален тогда и только тогда, когда C_k≤α_k для всех k. Начнем с выбора допустимого начального плана. Сразу видно, что допустимым является план х₁=1, х₂=1, х₃=0. Этот план опорный, так как векторы a₁ и a₂ линейно независимы - образуют базис.

Построим симплексную таблицу (табл. 4), найдя разложения по этому базису векторов a₃ и b.

Таблица 4

Вычислим величину

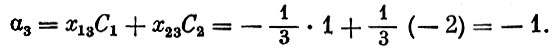
Разность 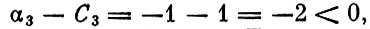следовательно, сходный план неоптимален. Для того чтобы его улучшить, необходимо ввести в базис вектор a₃. Так как мы хотим, чтобы и новый план был опорным, один из прежних векторов базиса должен быть из него исключен.

Разложение вектора a₃ по базису содержит лишь одну положительную компоненту. Следовательно,

Пользуясь приведенными выше формулами, определяем новый план. Имеем

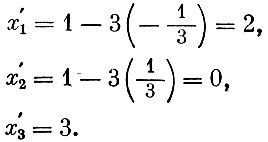
Проверим вновь полученный план на оптимальность. Для этого строим новую симплексную таблицу (табл. 5), используя соответствующие формулы преобразования.

Таблица 5

Величина α₂=x₁₂C₁+x₃₂C₃=1·1+3·1=4, а разность α₂-с₂=4+2=6>0. Следовательно, новый план х=(2, 0, 3) оптимален. Значение целевой функции в этом плане равно z₁=2-2·0+3=5. (Сравните: в первоначальном плане значение целевой функции равнялось z₀=1-2·1=-1.) Задача решена.

Описанный вариант симплекс-метода не является единственным. На практике обычно употребляется более совершенный вариант - модифицированный симплекс-метод, связанный с использованием двойственной задачи (о. о. оценок). Существуют и другие методы решения задач линейного программирования. Упомянем и коротко поясним один из них - метод блочного программирования, или, как его еще называют, принцип разложения.

При решении задач линейного программирования большой размерности постоянно приходится иметь в виду следующие два обстоятельства. Во-первых, решение задач с большим числом переменных и ограничений ведет к частому использованию устройств внешней памяти ЭВМ, которые характеризуются относительно невысоким быстродействием, что в конечном счете приводит к значительному расходу машинного времени. Во-вторых, очень часто возникающие из нужд практики задачи обладают той или иной специальной структурой (матрица ограничений симметрична, имеет блочную структуру, содержит много нулей и т. п.). Хотя сама задача в этом случае и не может быть решена с помощью специальных методов решения, но отдельные ее части - задачи меньшего объема - могут быть эффективно разрешены с помощью некоторых специальных методов.

Так вот, метод блочного программирования основан на разложении исходной задачи на отдельные подзадачи - блоки, для решения которых могут быть применены различные специальные методы в зависимости от вида блоков, и главную задачу - координирующую программу, которая связывает между собой все эти подзадачи. Такое разбиение делает возможным разновременное решение отдельных частей исходной задачи и позволяет тем самым меньше пользоваться внешней памятью ЭВМ. Многие задачи очень большой размерности, которые "не влезают" в современные машины, удалось впервые решить именно с помощью блочного программирования.

У этого метода довольно ясный экономический смысл. Если каждая подзадача характеризует деятельность одного предприятия некоторой отрасли, а координирующая программа содержит ограничения, относящиеся ко всем ресурсам в этой отрасли, то процесс решения примерно таков. Прежде всего решается главная задача и на основе этого решения строятся целевые функции для подзадач. Далее, порознь решаются все подзадачи, причем каждая имеет свою целевую функцию. На основании этих решений вносятся коррективы в главную задачу, и процесс повторятся снова. Доказано, что после конечного числа итераций принцип разложения приводит к оптимальному плану исходной задачи, если таковой существует.

В связи с решением задач большого объема следует отметить важность алгорифмического описания производственных способов. Поясним, что это означает. Для решения задачи линейного программирования в ЭВМ помимо алгорифма решения должны быть введены все производственные способы. Хранятся они в специальном запоминающем устройстве, носящем название памяти машины. Как правило, ЭВМ имеет два типа памяти - оперативную и внешнюю (магнитные барабаны, ленты), различающиеся скоростями воспроизведения имеющейся в них информации. Оперативная память обладает гораздо большим быстродействием, поэтому в целях экономии машинного времени желательно как можно больше информации держать именно в оперативной памяти. Если способов много и каждый из них описан индивидуально, то этот объем информации может быть настолько велик, что даже не поместится в память машины. Если же в ЭВМ введен алгорифм, правило, по которому она сама может по мере необходимости формировать способы, то это значительно повышает эффективность использования памяти ЭВМ, расширяет круг решаемых задач.

Наличие универсальных эффективных методов решения задач линейного программирования, носящих ясно выраженный алгорифмический характер (характер четкого предписания), позволяет успешно программировать и реализовать их решение на ЭВМ. Имеется большой набор программ для этой цели, дающих возможность решать задачи с числом ограничений порядка 100 и более и с сотнями и тысячами переменных (способов). Решение требует нескольких минут (иногда часов) машинного времени. Задачи меньшего объема теми же методами могут успешно решаться и вручную с применением настольных счетных машин.