8.3. Выбор объема производства на краткосрочный период

Как следует выбирать руководителю фирмы, максимизирующей прибыль, объем выпуска продукции на краткосрочный период при фиксированном размере капитала? Здесь мы покажем, как фирма может использовать информацию о доходах и издержках, чтобы принять решение по объему выпуска продукции, максимизирующее прибыль.

Максимизация прибыли

На краткосрочном отрезке времени фирма оперирует постоянным размером капитала и должна выбирать такой объем переменных факторов производства (труда и материалов), который максимизировал бы прибыль. Ввиду важности этого вопроса мы будем выводить объем выпуска продукции, максимизирующий прибыль, тремя различными способами: численным, графическим и алгебраическим.

Табл. 8.2 содержит информацию о доходах и издержках фирмы. Фирма продает свою продукцию на конкурентном рынке по рыночной цене 40 долл. за единицу независимо от количества реализуемой продукции. Заметим, что доход фирмы растет пропорционально объему выпуска продукции, так как средний доход (т. е. цена) является постоянной величиной. Постоянные издержки производства составляют 50 долл., а полные издержки растут вместе с объемом выпуска, как свидетельствуют данные табл. 8.2. Прибыль фирмы является разницей между доходом и полными издержками:

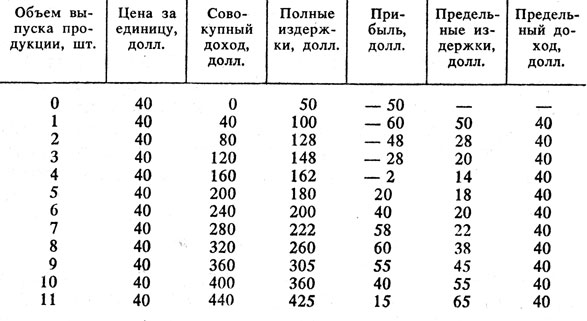
Таблица 8.2 Краткосрочные доходы и издержки фирмы

Для малых объемов выпуска продукции прибыль фирмы имеет отрицательную величину - доход недостаточен, чтобы возместить постоянные и переменные издержки. По мере увеличения объема производства прибыль становится положительной величиной и растет, пока объем выпуска продукции не достигнет 8 единиц. Выше 8 единиц прибыль падает, отражая опережающий рост полных издержек производства. Заметим, что прибыль максимизирована при q^* = 8, где MR близко к МС.

Рис. 8.3 показывает это графически. На рис. 8.3а изображен доход фирмы R(q) в виде прямой, проходящей через начало координат. Ее угловой коэффициент представляет собой отношение изменения дохода к изменению объема выпуска продукции, т. е. равен предельному доходу. Аналогичным образом угловой коэффициент линии полных издержек (ТС) представляет собой отношение изменения издержек производства к изменению объема выпуска продукции, т. е. предельные издержки.

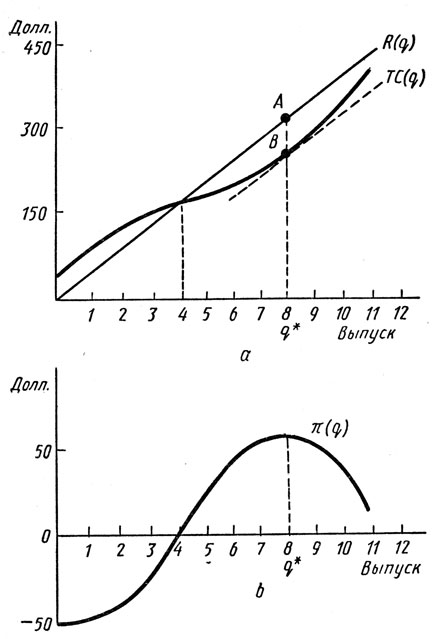
Рис. 8.3. График максимизации прибыли в краткосрочном периоде

На рис. 8.3b показана прибыль фирмы я, которая вначале имела отрицательную величину, затем достигла максимума при объеме выпуска продукции q^* = 8 и стала вновь снижаться. Отметим, что, когда прибыль максимизирована, расстояние между кривыми R и ТС (отрезок между точками А и В) самое большое. В этой точке угловой коэффициент кривой дохода (предельный доход) равен угловому коэффициенту кривой полных издержек (предельным издержкам). Таким образом, прибыль максимальна, когда предельный доход фирмы равен предельным издержкам производства. Это условие обязательно для всех фирм, будь они идеально конкурентны или нет.

Данное условие также вытекает из данных табл. 8.2. Для всех объемов выпуска продукции вплоть до 8 предельный доход выше предельных издержек. При любом объеме выпуска продукции до 8 единиц фирме следует наращивать выпуск, так как прибыль увеличивается. При выпуске продукции в 9 единиц, однако, предельные издержки становятся выше предельного дохода, и поэтому дополнительный объем производства скорее снизит, а не увеличит прибыль. В табл. 8.2 не показан объем выпуска продукции, при котором предельный доход в точности совпадает с предельными издержками. Вместе с тем из приведенных данных следует, что когда MR(q)>MC(q), объем выпуска продукции нужно наращивать, а когда MR(q)<С MC(q), - то сокращать. Если в табл. 8.2 можно было бы включить объемы выпуска в достаточно малых единицах, правило MR(q) = MC(q) соблюдалось бы в точности.

То же самое правило можно вывести алгебраически. Прибыль равна

и максимизируется в точке, в которой малый прирост объема производства оставляет прибыль без изменений (т. е. π(q)/Δq = 0):

Выражение ΔR(q)/Δq представляет собой отношение изменения дохода к изменению объема выпуска продукции, или предельный доход, а ΔТС(q)/Δq представляет собой предельные издержки. Таким образом, мы делаем вывод, что прибыль достигает максимума, когда

Максимизация прибыли конкурентной фирмой

Вспомним, что кривая спроса для фирмы на конкурентном рынке представляет собой горизонтальную линию, и, таким образом, предельный доход и цена равны: MR = Р. Следовательно, правило максимизации прибыли для конкурентной фирмы заключается в выборе такого объема выпуска продукции, чтобы цена равнялась предельным издержкам.

Правило для конкурентной фирмы:

Заметим, что это правило для выбора объема выпуска продукции, а не цены, поскольку конкурентная фирма воспринимает цену как заданную. Однако мы увидим в гл. 10, что это правило является полезным, когда мы сравниваем цену неконкурентной фирмы с той ценой, которая была бы, если бы рынок был конкурентным. Правило может также помочь при принятии решения об установлении цен, когда дело касается неконкурентных фирм.

Кривые предельного дохода и предельных издержек на рис. 8.4 также иллюстрируют данное правило максимизации прибыли. Кривые средних и предельных доходов проведены как горизонтальные линии при цене, равной 40 долл. На этом рисунке мы провели кривую средних издержек АС, кривую средних переменных издержек AVC и кривую предельных издержек МС для того, чтобы лучше показать прибыль фирмы.

Прибыль достигает максимума в точке А, связанной с объемом выпуска продукции q^* = 8 и ценой в 40 долл., так как в данной точке предельный доход равен предельным издержкам. При более низком объеме производства (скажем, q₁ = 7) предельный доход больше предельных издержек, и поэтому прибыль может быть дополнительно увеличена за счет увеличения выпуска продукции. Заштрихованная площадь между q₁ = 7 и q^* показывает потерянную прибыль, связанную с производством при q₁. При более высоком объеме выпуска продукции (скажем, q₂) предельные издержки выше предельного дохода. В этом случае сокращение объема выпуска продукции дает экономию издержек, превышающих предельный доход. Заштрихованная площадь между q^* и q₂ = 9 показывает потерянную прибыль, связанную с производством на уровне q₂.

Кривые MR и МС пересекаются как при объеме производства q₀, так и при объеме q^*. При qo, однако, прибыль явно не достигает максимума. Увеличение объема производства выше Q₀ увеличивает прибыль, так как справа от Q₀ предельные издержки значительно ниже предельного дохода. Поэтому условием максимизации прибыли является равенство предельного дохода предельным издержкам в точке, в которой кривая предельных издержек возрастает, а не снижается.

Получение прибыли конкурентной фирмой в краткосрочном периоде

Рис. 8.4 показывает также прибыль конкурентной фирмы в краткосрочном периоде. Расстояние АВ представляет собой разницу между ценой и средними издержками при объеме выпуска продукции q^* и равно средней прибыли на единицу выпуска продукции. Отрезок ВС измеряет общее количество произведенной продукции. Следовательно, прямоугольник ABCD отражает валовую прибыль.

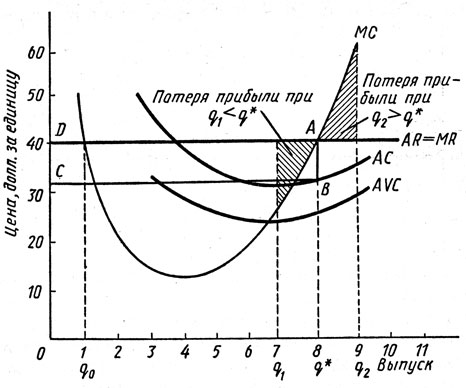
Рис. 8.4. График максимизации прибыли конкурентной фирмой

Фирме не всегда нужно максимизировать прибыль на краткосрочном отрезке, как показывает рис. 8.5. Главным отличием от рис 8.4 являются увеличенные постоянные издержки производства. Это поднимает средние полные издержки, но не меняет кривых средних переменных и предельных издержек. При максимизирующем прибыль периоде объеме производства q^* цена Р меньше, чем средние издержки, и поэтому отрезок линии АВ равен средним убыткам производства. Аналогичным образом заштрихованный прямоугольник ABCD представляет убытки фирмы.

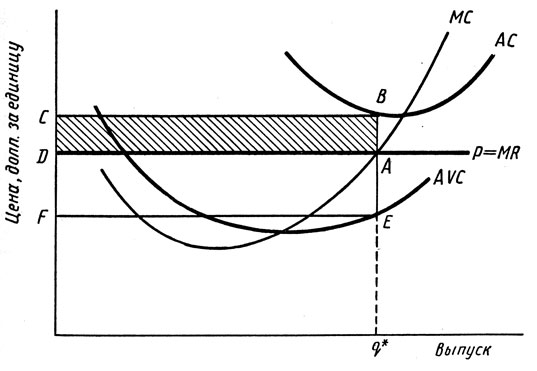
Рис. 8.5. График убытков конкурентной фирмы в краткосрочном

Почему же фирма, терпящая убытки, не прекращает производство? На краткосрочном отрезке фирма может работать с убытками, потому что она рассчитывает на получение прибыли в будущем по мере роста цены ее продукции или снижения издержек производства. Фактически в краткосрочном периоде перед фирмой стоит двоякий выбор: она может производить некоторое количество продукции или временно закрыть свое производство. Она выберет более прибыльную из двух альтернатив. В частности, фирма решит закрыть производство (ничего не выпускать), когда цена ее товара меньше минимальных средних переменных издержек. В данной ситуации прибыль от производства не покроет переменных издержек и убытки возрастут.

Рис. 8.5 показывает случай, при котором выпуск продукции желателен. Объем производства q^* минимизирует краткосрочные убытки. В данном случае дешевле произвести продукцию объемом q^*, чем вообще не производить продукции, так как при q^* цена превышает средние переменные издержки. Каждая произведенная единица продукции дает доход, превышающий издержки, и тем самым более высокую прибыль, чем если бы фирма не производила ничего. (Валовая прибыль, однако, остается все еще отрицательной величиной, так как постоянные издержки высоки.) Отрезок линии АЕ измеряет разницу между ценой и средними переменными издержками и прямоугольник AEFD - дополнительную прибыль, которая может быть получена при объеме производства, равном q^*, а не нулю.

Чтобы увидеть это другим способом, вспомним, что разница между средними издержками АС и средними переменными издержками AVC является средними постоянными издержками AFC. Следовательно, на рис. 8.5 отрезок линии BE представляет собой средние постоянные издержки, прямоугольник CBEF представляет собой полные постоянные издержки производства. Когда фирма ничего не производит, ее убытки равны ее полным постоянным издержкам CBEF. Но когда она производит объем продукции q^*, ее убытки сокращены до величины прямоугольника ABCD. Постоянные издержки, не имеющие отношения к производственным решениям фирмы в краткосрочном периоде, являются решающими при определении стратегии фирмы на долговременный период.

Таким образом, конкурентная фирма не выпускает продукции, если цена меньше минимальных средних переменных издержек. Когда фирма производит продукцию, она максимизирует прибыль, выбирая такой объем производства, при котором цена равна предельным издержкам. При данном объеме выпуска продукции прибыль является положительной величиной, если цена выше средних валовых издержек. Фирма может действовать с убытками в краткосрочном периоде. Однако если фирма сталкивается с убытками и на долговременном этапе, она прекратит производство.

Пример 8.1. Некоторые соображения об оценке издержек для руководителей

Применение правила о том, что предельный доход должен быть равен предельным издержкам, зависит от способности руководителя оценивать предельные издержки. Чтобы правильно оценить издержки, руководителям следует помнить три основных момента.

Во - первых, не используйте средние переменные издержки вместо или в качестве приблизительного значения предельных издержек. Когда предельные и средние издержки почти постоянны, между ними почти нет разницы. Однако когда предельные и средние издержки резко возрастают, применение средних переменных издержек может привести к значительным ошибкам при принятии решений об объеме производства. Предположим, например, что компания располагает следующей информацией об издержках.

Текущий выпуск продукции: 100 единиц в день, из них 25 единиц производится в сверхурочное время.

Материальные издержки: 500 долл. в день.

Заработная плата: 2000 долл. в день (тариф) плюс 1000 долл. в день (доплата за сверхурочную работу).

Средние переменные издержки легко подсчитать: это заработная плата и материальные издержки (3500 долл.), деленные на 100 единиц в день, или 35 долл. за единицу продукции. Но нам необходимо знать предельные издержки, которые можно подсчитать следующим образом: вероятнее всего, материальные затраты на единицу продукции должны быть постоянными независимо от объема выпуска продукции, и следовательно, предельные материальные издержки составляют 500 долл./100 = 5 долл. на единицу. Так как предельные издержки на зарплату предположительно связаны только со сверхурочной работой, их вычисляют исходя из того, что 25 из 100 единиц продукции были получены в сверхурочное время. Средняя сверхурочная плата 1000 долл./25 = 40 долл. за единицу продукции дает хорошую оценку предельных издержек на зарплату. Таким образом, предельные издержки производства дополнительной единицы продукции составляют 45 долл. (предельные материальные и трудовые затраты), что существенно выше средних переменных издержек в 35 долл. Если руководитель полагается на средние переменные издержки, может быть произведено слишком много продукции.

Во - вторых, тот или иной показатель в бухгалтерском учете фирмы может состоять из двух компонентов, лишь один из которых связан с предельными издержками. Предположим, например, что руководитель пытается сократить объем производства. Он сокращает продолжительность работы некоторых рабочих и временно увольняет других. Но зарплата временно уволенным рабочим может оказаться неточным измерителем предельных издержек производства, так как профсоюзные трудовые соглашения зачастую требуют, чтобы фирма выплачивала временно уволенным служащим часть зарплаты.

В - третьих, все вмененные издержки должны включаться в состав предельных издержек. Предположим, универсальный магазин принимает решение о продаже детской мебели. Вместо строительства новой торговой площади управляющий решает использовать часть третьего этажа, предназначавшегося для бытовой техники. Предельные издержки использования данного помещения составляют прибыль, которая могла бы быть получена, если бы магазин продолжал продавать на этом месте бытовую технику, на единицу проданной мебели. Эти вмененные издержки могут быть существенно выше арендной платы, которую магазин вносит за указанную часть здания.

Вот те три момента, которые могут помочь руководителю правильно подсчитать предельные издержки. Если не учитывать этого, производство может оказаться слишком большим или малым и тем самым сократится прибыль.

дебетовые карты с бесплатным обслуживанием