6.4. Производство с двумя переменными вводимыми факторами

Теперь, когда мы ознакомились с взаимосвязями между производством и производительностью, рассмотрим производственную стратегию фирмы в долговременный период с двумя (а не одним) переменными факторами. Мы можем изучить альтернативные производственные варианты, посмотрев на форму группы изоквант.

Изокванты на рис. 6.4 воспроизведены с рис. 6.1. Все они имеют наклон вниз, так как труд и капитал имеют положительные предельные продукты. Большее количество того или иного производственного фактора увеличивает выпуск продукции. Поэтому если выпуск продукции должен поддерживаться постоянным, то чем больше используется один фактор, тем меньше будет использоваться другой.

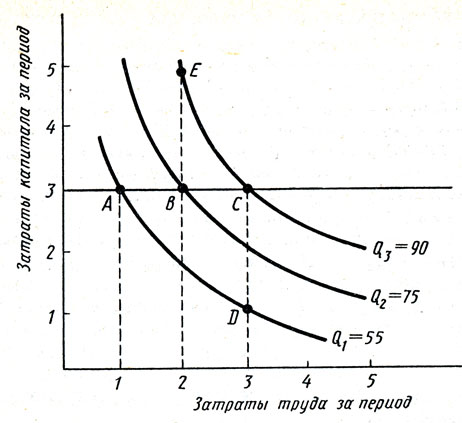
Рис. 6.4. Формы изоквант

Убывающая отдача

В данном случае как по отношению к труду, так и по отношению к капиталу действует закон убывающей отдачи. Чтобы увидеть, почему, например, сокращается отдача от труда, проведем горизонтальную линию, фиксирующую использование капитала на определенном уровне, скажем 3 единицы. Подсчитывая данные об объеме выпуска продукции по каждой изокванте по мере роста трудозатрат, мы отмечаем, что каждая дополнительная единица труда дает все меньший и меньший прирост выпуска продукции. Так, когда трудовые затраты возрастают с 1 до 2 единиц (от А к В), выпуск продукции повышается на 20 единиц (с 55 до 75). Однако когда трудовые затраты возрастают еще на одну дополнительную единицу (от В к С), выпуск продукции повышается лишь на 15 единиц (с 75 до 90). Таким образом, закон убывающей отдачи действует по отношению к труду как в долговременные, так в краткосрочные периоды. Увеличение использования одного фактора при фиксированном положении другого приводит ко все более и более низкому приросту выпуска продукции, а изокванта становится все круче по мере замещения труда капиталом и все более плоской, когда капитал замещается трудом.

Закон убывающей отдачи действует и по отношению к капиталу. При фиксированных трудозатратах предельный продукт капитала снижается по мере роста капитала. Например, когда капитал вырос с 1 до 2 единиц, а трудозатраты зафиксированы на уровне 3 единиц, предельный продукт капитала первоначально равен 20 единицам (75 - 55), но снижается до 15 единиц (90 - 75), когда затраты капитала увеличиваются с 2 до 3 единиц.

Заменяемость производственных факторов

Угловой коэффициент каждой изокванты указывает, каким образом происходит замещение одного фактора производства другим при сохранении постоянного объема продукции. Абсолютное значение углового коэффициента называется предельной нормой технологического замещения (MRTS). MRTS труда капиталом представляет собой величину, на которую может быть сокращен капитал за счет использования одной дополнительной единицы труда при фиксированном объеме выпуска продукции. Она аналогична предельной норме замещения (MRS), упоминавшейся в теории потребления. Подобно MRS MRTS всегда является положительной величиной. В математической форме MRTS = - изменение величины используемого капитала/ изменение трудозатрат, или

где ΔК и ΔL представляют собой относительно небольшие изменения капитала и труда для отдельной изокванты (т. е. для постоянного Q).

Заметим, что на рис. 6.5 предельная норма технологического замещения ( - ΔК/ΔL) равна 2, когда затраты труда увеличиваются с 1 единицы до 2 и выпуск продукции фиксируется на уровне 75 единиц. Однако MRTS снижается до 1, когда затраты труда возрастают с 2 до 3, а впоследствии уменьшаются с 2/3 до 1/3. Ясно, что чем больше труда замещается капиталом, тем менее производительным становится труд, а использование капитала становится относительно более эффективным. Поэтому чтобы сохранить постоянным объем выпуска продукции, необходимо сократить минимальное количество капитала, в этом случае изокванта приобретает более плоскую форму.

Изоквантные кривые имеют вогнутую форму - MRTS сокращается по мере движения вниз вдоль изокванты. Уменьшение предельной нормы технического замещения говорит о том, что эффективность использования любого производственного фактора ограничена. По мере замещения в производственном процессе капитала большим количеством труда производительность труда снижается. Аналогичным образом когда труд замещается большим количеством капитала, его отдача снижается. Производству требуется сбалансированное сочетание обоих производственных факторов.

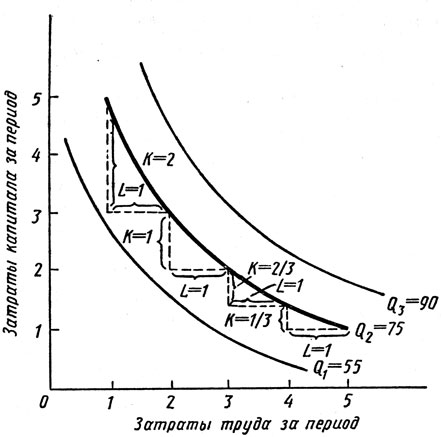
Рис. 6.5. Предельная (маргинальная) норма технического замещения

Как мы и предполагали, MRTS тесно связана с предельными продуктами труда MP_L и капитала МР_К. Чтобы показать это, представим, что при некотором увеличении трудозатрат и сокращении используемого количества капитала объем выпуска продукции остается постоянным. Прирост выпуска продукции в результате увеличения затрат труда равен величине дополнительного выпуска продукции, приходящегося на дополнительную единицу труда (предельному продукту труда), помноженной на количество дополнительных единиц труда: Объем дополнительного выпуска в результате увеличения трудозатрат = (MP_L) (ΔL).

Аналогичным образом снижение выпуска продукции в результате сокращения используемого капитала представляет собой сокращение объема выпуска в результате сокращения капитала на 1 единицу (предельный продукт капитала), помноженный на число сокращенных единиц капитала; сокращение выпуска в результате уменьшения капитала = (MP_K) (ΔК).

Так как мы сохраняем объем выпуска продукции постоянным для всей изокванты, изменение объема выпуска продукции равно нулю. Таким образом:

Теперь, меняя условия, мы видим, что

Уравнение (6.2) говорит о том, что для отдельной изокванты непрерывное замещение капитала трудом в производственном процессе приводит к росту предельного продукта капитала и уменьшению предельного продукта труда. Общим результатом обоих изменений является тенденция к снижению предельной нормы технического замещения и выравниванию изокванты.

Производственные функции - два особых случая

Чтобы учесть возможные границы замещения одних факторов другими в производственном процессе, можно использовать два особых случая производственных функций. В первом, показанном на рис. 6.6, факторы идеально взаимозаменяемы. Здесь MRTS постоянна на всех точках изокванты. В данном случае один и тот же объем выпуска продукции может производиться только трудом, только капиталом или сочетанием того и другого. Например, объем выпуска продукции Q может быть достигнут за счет использования только капитала (в точке А), только труда (в точке С) или обоих производственных факторов (в точке В). Обычно это нереально, но в ряде случаев дает разумное приближение к производственному процессу фирмы. Например, телефон - автомат на дороге или на мосту может обслуживаться автоматически или техническим персоналом. Другим примером является процесс изготовления музыкальных инструментов, который может быть полностью основан на автоматизированном машинном производстве или на высококвалифицированном труде.

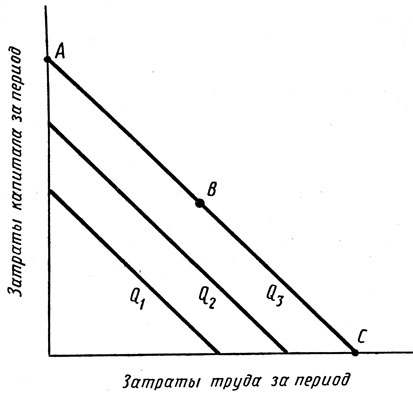
Рис. 6.6. Характер изменения производственной функции, когда факторы производства идеально заменяемы

Рис. 6. 7 показывает прямо противоположный случай - производственную функцию с фиксированной структурой использования факторов. В данном случае замещение одного фактора другим невозможно. Каждый объем выпуска продукции требует сочетания труда и капитала в определенной пропорции. Прирост выпуска нельзя получить без увеличения трудозатрат и капитала в определенной пропорции. В итоге изокванты на рис. 6. 7 имеют форму прямого угла. Примером такой функции может служить реконструкция бетонных прогулочных дорожек с использованием отбойного молотка. Повышение производительности труда не произойдет при использовании двух рабочих и одного отбойного молотка или двух отбойных молотков и одного рабочего. Другой пример - обслуживание такси, когда при обычных условиях нужны только один водитель и одна машина.

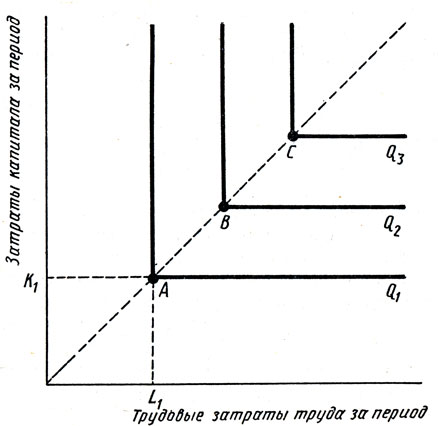
Рис. 6.7. Производственная функция с фиксированной структурой использования факторов

На рис. 6. 7 точки А, В и С представляют собой технически эффективные сочетания вводимых факторов. Например, чтобы произвести объем продукции Q₁, используется количество труда L₁ и капитала K₁ в точке А. Если капитал остается фиксированным на K₁, увеличение трудозатрат не изменит объем выпуска продукции. Не приведет к этому и увеличение капитала при фиксированных на L₁ затратах труда. Таким образом, на вертикальном и горизонтальном отрезках прямоугольных изоквант и предельный продукт труда, и предельный продукт капитала равны нулю. Выпуск продукции увеличивается только тогда, когда возрастает использование как труда, так и капитала, т. е. при движении от сочетания производственных факторов А к сочетанию В.

Производственная функция с фиксированной структурой использования факторов описывает ситуации, при которых фирма ограничена в выборе способа производства. Например, постановка телевизионного спектакля может быть связана с определенным сочетанием капитала (камера, звуковое оборудование и т. п.) и труда (режиссер, актеры и т. д.). Чтобы увеличить число телевизионных спектаклей, должны быть пропорционально увеличены все производственные факторы. В частности, сложно увеличить затраты капитала за счет снижения трудозатрат, так как актеры являются необходимым фактором производства (за исключением, вероятно, фильмов о животных). Точно так же сложно заменить трудом капитал, так как постановка фильмов и спектаклей требует весьма непростого оборудования.

Пример 6.3. Производственная функция для выращивания пшеницы

Урожай может быть получен различными методами. Продукты питания на крупных фермах в США обычно производятся капиталоемким способом, который характеризуется существенными капиталовложениями (в здания, оборудование) и относительно небольшими трудовыми затратами. Однако продукты питания могут производиться также при очень небольших капиталовложениях (мотыга) и огромных трудозатратах (несколько человек, испытывающих огромную тягу к земле). Одной из форм описания сельскохозяйственной производственной функции является изокванта (или несколько изоквант), которая показывает все сочетания производственных факторов, обеспечивающих определенный объем выпуска продукции (или несколько таких объемов). Нижеследующее описание производственной функции для пшеницы основано на статистических данных.

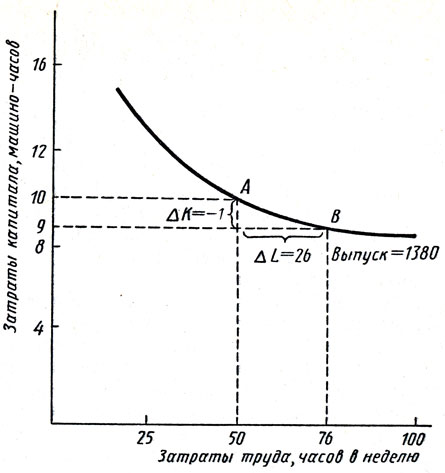
Рис. 6.8. Изокванта, описывающая производство пшеницы

На рис. 6. 8 изображена одна изокванта, связанная с производственной функцией, которая соотносится с объемом выпуска продукции 1380 бушелей пшеницы в неделю. Управляющий фермой может использовать данную изокванту, чтобы решить, будет ли выгодно нанять больше рабочих или применить больше техники. Предположим, ферма действует сейчас на точке А с трудозатратами L в 50 ч и затратами капитала К в 10 машино - ч. Управляющий решает сократить на 1 ч машинное время. Чтобы производить тот же объем работ в неделю, ему потребуется заменить данное машинное время путем увеличения трудозатрат на 26 ч.

Результаты подобного эксперимента подскажут фермеру форму изокванты для производства пшеницы. При сравнении точек А ( где L = 50, К = 10) и В (где L = 76, К = 9) на рис. 6.8, обе из которых находятся на той же изокванте, фермер обнаружит, что предельная норма технического замещения равна 0,04:

MRTS объясняет фермеру природу замещения капитала трудом. Так как MRTS значительно меньше 1, фермер знает, что, когда зарплата рабочего равна издержкам на эксплуатацию техники, ему следует использовать больше капитала (при нынешнем уровне производства ему необходимо 26 единиц труда, чтобы заменить 1 единицу капитала). Фактически он знает, что до тех пор, пока труд не станет значительно дешевле использования машин, производственный процесс останется капиталоемким.

Невозможно решить, какое количество рабочих нанять и сколько машин использовать, пока мы не рассмотрим вопросы издержек производства, о чем пойдет речь в следующей главе. Однако этот пример показывает, как знание изоквант и предельной нормы технического замещения может помочь фермеру. Оно также помогает понять, почему большинство ферм в США и Канаде, где труд относительно дорог, действует в таких масштабах производства, при которых MRTS относительно низка (с высоким соотношением капитала и труда), тогда как на фермах в развивающихся странах, где используется дешевый труд, MRTS высока (и низко соотношение капитала и труда). Точное соотношение труда и капитала зависит от стоимости издержек - вопрос, к которому мы вернемся в гл. 7.

кредитная карта