2.5. Оценка и прогнозирование последствий изменения рыночных условий

Мы обсудили значение и характеристики спроса и предложения, но исходили в основном из качественного подхода. Чтобы использовать кривые предложения и спроса для анализа и прогнозирования последствий изменения рыночных условий, мы должны придать им численное значение. Например, чтобы увидеть, как сокращение на 50 % объема предложения бразильского кофе может повлиять на мировую цену кофе, нам надо построить фактические кривые спроса и предложения и рассчитать, как сместятся кривые и как затем изменятся цены.

В данном разделе мы увидим, как сделать простые расчеты с помощью линейных кривых предложения и спроса. Мы используем линейные кривые, которые являются аппроксимацией более сложных кривых, потому что с ними легче работать. Это может показаться удивительным, но возможен содержательный экономический анализ отдельных данных на клочке бумаги с помощью карандаша и карманного калькулятора.

Прежде всего мы должны научиться строить линейные графики предложения и спроса в соответствии с данными рынка. (Под этим мы не подразумеваем статистические вычисления на основе линейной регрессии или других статистических методов, которые мы рассмотрим ниже.) Предположим, у нас имеются два вида величин по какому - нибудь отдельному товару: цена и количество, которые в целом доминируют на рынке (т. е. такие цена и количество, которые превалируют в среднем, или когда на рынке наблюдается равновесие, или при которых рыночные условия считаются "нормальными"). Мы называем эти величины равновесными ценой и количеством и обозначаем их буквами Р^* и Q^*. Эластичность предложения и спроса от цены для данного товара (в точке равновесия или вблизи нее) мы обозначаем буквами E_S и E_D.

Эти числовые данные могут быть взяты из какого - то статистического исследования, это могут быть данные, относительно которых мы полагаем, что они обоснованы, или данные, которые мы хотим опробовать в ходе эксперимента. Все, что мы хотим сделать, - это построить кривые предложения и спроса, согласованные с этими данными. Тогда мы сможем определить численно сдвиги и в предложении, и в спросе, и в рыночной цене и количестве данного товара в зависимости от изменения таких переменных, как валовой национальный продукт, цена другого товара и отдельные издержки производства.

Начнем с линейных зависимостей, показанных на рис. 2.16. Их уравнения записываются так:

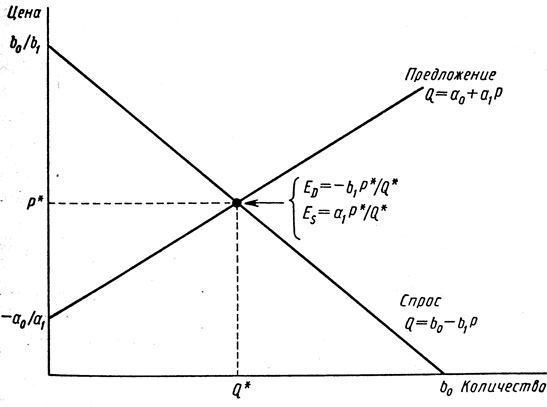
Рис. 2.16. Графики предложения и спроса, полученные экспериментальным путем

Предложение: Q = а₀ + a₁P. (2.4 а)

Спрос: Q = b₀ - b₁P. (2.4 b)

Проблема заключается в подборе значений констант а₀, a₁, b₀, b₁. Для кривых предложения и спроса этот подбор совершается в два этапа.

Первый этап. Вспомним, что эластичность предложения или спроса от цены может быть записана как

где ΔQ/ΔP - изменение в требуемом или предлагаемом количестве в результате небольшого изменения цены. Для линейной зависимости отношение ΔQ/ΔP является постоянной величиной. Из уравнений 2.4 а и 2.4 b мы видим, что для предложения ΔQ/ΔP =a₁ и для спроса ΔQ/ΔР = - b₁. Теперь подставим эти величины вместо ΔQ/ΔP в формуле эластичности:

Предложение: E_S = a₁ (P^*/Q^*). (2.5 а)

Спрос: E_D = - b₁ (P^*/Q^*). (2.5 b)

Здесь P^* и Q^* являются равновесными ценой и количеством, по которым мы располагаем данными и по которым строятся кривые. Так как мы располагаем значениями E_S, Е_D, Р^* и Q^*, мы можем подставить их в уравнения 2.5 а и 2.5 b и вычислить a₁ и b₁.

Второй этап. Так как теперь мы знаем a₁ и b₁, мы можем подставить эти значения вместе со значениями Р^* и Q^* в уравнения 2.4 а и 2.4 b и решить эти уравнения относительно а₀ и b₀. Например, мы можем переписать уравнение 2.4 а как

а затем использовать наши данные о Q^* и Р^* совместно со значениями a₁, вычисленными на первом этапе, и получить а₀.

Теперь обратимся к конкретному примеру - долговременным предложению и спросу на мировом рынке меди. Соответствующими значениями для данного рынка будут следующие: количество Q^* = 7,5 млн. метрических т/год, цена Р^* = 75 центов за фунт, эластичность предложения E_S = 1,6, эластичность спроса E_D = - 0,8 (цена меди колебалась за прошедшее десятилетие от 50 центов до 1,20 долл. и выше, но 75 центов - разумная средняя цена на 1980 - 1986 гг.).

Начнем с уравнения кривой предложения (2.4 а) и используем двухэтапную процедуру, чтобы вычислить значения а0 и a1. Долговременная эластичность предложения по цене равна 1,6, Р^* = 0,75, Q^* = 7,5.

Первый этап. Подставим эти величины в уравнение 2.5 а, чтобы получить a₁:

1,6 = a₁ (0,75/7,5) = 0,la₁ и отсюда a₁ = 1,6/0,1 = 16.

Второй этап. Подставим это значение вместо a₁ одновременно со значениями Р^* и Q^* в уравнение 2.4 а, чтобы определить а₀:

отсюда а₀ = 7,5 - 12 = - 4,5. Мы знаем теперь величины а₀ и a₁ и можем записать уравнение нашей кривой предложения:

Предложение: Q = - 4,5 + 16Р.

Следуя тому же порядку, обратимся к уравнению кривой спроса 2.4 b. Расчет долговременной эластичности спроса дает - 0,8. Вначале, чтобы определить b₁, подставим это значение, а также Р^* и Q^* в уравнение 2.5 b:

- 0,8 = - b₁ (0,75/7,5) = - 0,1 b₁, следовательно, b₁ = 0,8/0,1 = 8.

Затем подставим значение b₁, а также величины Р^* и Q^* в уравнение 2.4 b, чтобы определить b₀:

7,5 = b₀ - (8) (0,75) = b₀ - 6,

отсюда b₀ = 7,5 + 6 = 13,5. Таким образом, наша кривая спроса выражается так:

Спрос: Q = 13,5 - 8Р.

Чтобы проверить, не сделали ли мы ошибки, приравняем предложение и спрос и вычислим равновесную цену. Получим:

Предложение = - 4,5 + 16Р = 13,5 - 8 Р = Спрос 16Р + 8Р = 13,5 + 4,5

или Р = 18/24 = 0,75, что действительно представляет собой равновесную цену.

Мы считали, что предложение и спрос зависят только от цены. Но они могут также зависеть и от других переменных. Например, спрос может зависеть и от дохода, и от цены. Тогда функция спроса запишется так:

где I - индекс совокупного дохода или валового национального продукта. (Например, I может равняться единице в базовом году, а затем увеличиваться или уменьшаться, отражая процент увеличения или снижения совокупного дохода.)

Для нашего примера с рынком меди допустимым оценочным значением долговременной эластичности дохода от спроса будет 1,3. При линейной кривой спроса (2.6) мы можем вычислить b₂, используя формулу эластичности спроса от дохода: Е = (I/Q) (ΔQ/ΔI). Принимая за базовое значение I = 1,0, мы имеем 1,3 = (1,0/7,5) (b₂) и b₂ = (1,3) (7,5) (1,0) = 9,75. Наконец, подставив b₁ = 8, b₂ = 9,75, Р^* = 0,75 и Q^* = 7,5 в 2.6, мы можем определить, что b₀ должно равняться 3,75.

Мы видели, как строятся линейные зависимости предложения и спроса в соответствии с расчетными данными. Чтобы посмотреть, как эти кривые могут быть использованы для анализа рынков, обратимся к примеру 2.5, посвященному поведению цен на медь, и к примеру 2.6, рассматривающему мировой нефтяной рынок.

Пример 2.5. Снижение спроса и цен на медь

После достижения уровня около 1 долл. за фунт в 1980 г. цена меди резко снизилась до 60 центов за фунт в 1986 г. В реальном (с поправкой на инфляцию) выражении эта цена была даже ниже, чем во время Великой депрессии. Рис. 2.17 показывает поведение сопоставимых и действующих цен на медь в 1965 - 1986 гг.

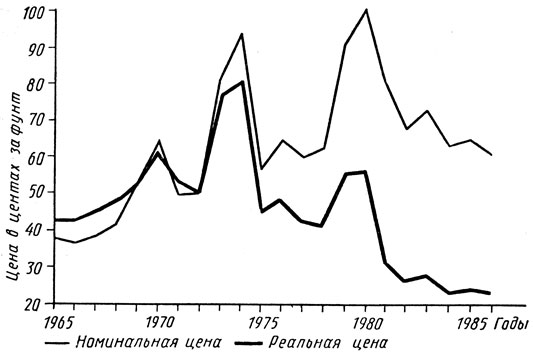
Рис. 2.17. График изменения рыночных цен на медь в 1965 - 1985 гг.

Экономические спады мирового масштаба в 1980 и 1982 гг. также сказались на снижение цен на медь. Как показано выше, эластичность спроса на медь от цены составляет 1,3. Но спрос на медь не стал повышаться, хотя промышленное производство оживилось к середине 80 - х годов. Вместо этого мы стали свидетелями глубокого спада спроса на медь.

Данный спад произошел по двум причинам. Во - первых, значительная часть потребления меди идет на изготовление электрогенерирующего оборудования и передачу электроэнергии. Но к концу 1970 г. в большинстве промышленно развитых стран темпы роста производства электроэнергии серьезно снизились (в США, к примеру, с 6 % в год в 60 - е годы до менее 2 % в конце 70 - х - 80 - е годы). Это означало спад в той отрасли, которая была крупным потребителем меди. Во - вторых, в 80 - х годах медь все успешнее заменялась другими материалами (алюминием и оптическим волокном).

Как спад спроса на медь повлияет на ее цену? Этот вопрос был предметом серьезной озабоченности фирм, работавших в медедобывающей промышленности. Многим из них пришлось закрыть предприятия или остановить добычу в связи с мрачной перспективой установления низких цен. Мы можем использовать линейные функции предложения и спроса, только что выведенные нами, чтобы ответить на этот вопрос. Каково воздействие на цену при спаде спроса на 20 %? Так как мы здесь не касаемся влияния валового национального продукта на рост, можно исключить из уравнения спроса слагаемое b₂I.

Мы хотим сместить кривую спроса влево на 20 %. Другими словами, мы хотим, чтобы требуемое количество составляло 80 % прежнего для каждого значения цены. В нашей линейной зависимости спроса мы просто умножаем правую сторону уравнения на 0,8:

Предложение: Q = - 4,5 + 16Р. Теперь мы можем приравнять предложение и спрос и определить цену:

или Р = 15,3/22,4 = 68,3 цента за фунт. Следовательно, спад спроса на 20 % влечет снижение цены примерно на 7 центов за фунт, или на 10 %.

Пример 2.6. Мировой рынок нефти

С 1974 г. на мировом рынке нефти доминировал картель ОПЕК. За счет коллективного сдерживания выпуска продукции ОПЕК преуспел в поддержании цен на нефть выше того уровня, который мог бы быть на конкурентном рынке. Члены ОПЕК смогли сделать это, потому что на их долю приходилась большая часть мировой добычи нефти (около 2/3 в 1974 г.).

В гл. 12 мы более подробно остановимся на стратегии ценообразования ОПЕК как составной части нашего анализа картелей и поведения картелизированного рынка. А теперь посмотрим, как простые линейные кривые предложения и спроса можно использовать для прогнозирования последствий сокращения объема добычи нефти со стороны ОПЕК на кратковременном и долговременном отрезках времени.

Так как этот пример относится к 1973 - 1974 гг., все цены измеряются в долларах 1974 г., которые в связи с инфляцией стоили больше сегодняшних. Приведем несколько цифр: мировая цена нефти в 1973 г. была равна 4 долл. за баррель, мировые спрос и общее предложение составили 18 млрд. баррелей в год, предложение ОПЕК в 1973 г. - 12 млрд. баррелей в год, а предложение конкурирующих (не членов ОПЕК) продавцов равнялось 6 млрд. баррелей в год. Приведем некоторые расчеты эластичности предложения и спроса от цены, совместимые с линейными зависимостями предложения и спроса:

Вы должны убедиться, что эти величины означают для спроса и конкурентного предложения на кратковременном отрезке следующее:

Кратковременный спрос: D = 18,9 - 0,225Р.

Кратковременное конкурентное предложение: S_С = 5,4 + 0,15Р.

Конечно, совокупное предложение включает конкурентное предложение плюс предложение ОПЕК, которое мы рассматриваем как постоянное в 12 млрд. баррелей в год. Добавив эти 12 млрд. баррелей в год к вышеозначенной кривой конкурентного предложения, получим общее кратковременное предложение S_T = 17,4 + 0,15Р.

Вы должны проверить, что спрос и общее предложение равны при цене 4 долл. за баррель.

Вам следует также удостовериться, что соответствующие выражения для функций спроса и предложения на долговременном отрезке имеют вид:

Долговременный спрос: D = 25,2 - 1,8Р.

Долговременное конкурентное предложение: S_C = 3,6 + 0,6Р.

Общее долговременное предложение: S_T = 15,6 + 0,6Р.

Снова вы можете проверить, что предложение и спрос уравниваются при цене 4 долл. за баррель.

Теперь подсчитаем, что произойдет, если ОПЕК снизит производство на ¼, или на 3 млрд. баррелей в год. Для кратковременного отрезка просто вычтем 3 из общего, или совокупного, предложения:

Кратковременный спрос: D = 18,9 - 0,225Р.

Общее кратковременное предложение: S_T = 14,4 + 0,15Р.

Уравнивая это общее предложение со спросом, мы видим, что на кратковременном отрезке цена поднимется до 12 долл. за баррель, - фактически так и произошло. Рис. 2.18 показывает сдвиг в предложении и его воздействие на цену. Первоначальное равновесие находится на пересечении S_общ и D. После снижения производства со стороны ОПЕК равновесие устанавливается в точке, где пересекаются S_общ и D.

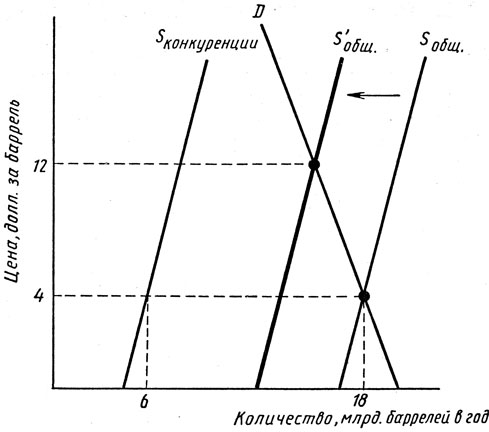
Рис. 2.18. График равновесия на рынке нефти после сокращения производства в ОПЕК

На долговременном отрезке, однако, дела будут обстоять иначе. Из - за того, что как спрос, так и конкурентное предложение более эластичны на длительном отрезке, сокращение производства нефти ОПЕК на ¼ больше не будет удерживать цену на уровне 12 долл. за баррель. Вычтя 3 из объема долговременного общего предложения и приравняв эту величину долговременному спросу, мы увидим, что цена составит лишь 5,25 долл. Это на 1,25 долл. выше старой цены в 4 долл., но значительно ниже 12 долл.

Следует ожидать резкого увеличения цены и ее постепенного снижения впоследствии, по мере того, как падает спрос и растет конкурентное предложение в ответ на цену. Так и происходило вплоть до 1979 г. Но в течение 1979 - 1980 гг. цена на нефть опять подскочила вверх. Что произошло? Революция в Иране и война между Ираном и Ираком. Сокращение на 1,5 млрд. баррелей в год производства иранской нефти и почти на 1 млрд. баррелей - иракской нефти привело к дальнейшему росту цен на нефть, что стало благом для других членов ОПЕК.

Хотя ирано - иракская война продолжалась, к 1986 г. цены на нефть упали, став значительно ближе к конкурентному уровню. Это произошло в основном благодаря долговременной реакции спроса и конкурентного предложения.

По мере снижения спроса и расширения конкурентного предложения доля ОПЕК на мировом рынке упала почти до 1/3 по сравнению с 2/3 в 1973 г.

заказать кредитную карту