§ 8. Задача о замене оборудования

Одной из важных проблем, с которой приходится встречаться почти во всех отраслях производственной деятельности - в промышленности и науке, на транспорте, в торговле, сельском хозяйстве и т. д.- является проблема оптимальной политики замены оборудования. Суть этой проблемы состоит в том, что в каждом конкретном случае надо уметь определить такой момент, когда выгоднее купить новое оборудование, чем эксплуатировать старое. Критерии, используемые для определения оптимальности р замене оборудования, могут быть весьма различными. Например, в промышленности обычный критерий, используемый для определения оптимальной политики замены оборудования, состоит в минимизации ожидаемых затрат или максимизации ожидаемой прибыли за некоторый промежуток времени. Часто в задачах о замене оборудования важным фактором является технический прогресс. В большей Шли меньшей степени этот фактор также может учитываться, однако зачастую это оказывается сделать трудно по той причине, что результаты технического прогресса невозможно точно предсказать.

Рассмотрим кратко постановку таких задач [8, 12]. Пусть требуется выработать оптимальную политику замены оборудования исходя из требования свести к минимуму ожидаемые затраты за некоторый промежуток времени. Будем считать, что подобные решения принимаются периодически, например раз в год. Предположим также, что оборудование может эксплуатироваться неограниченно долго, если травить достаточные средства на его ремонт, и решение о замере старого оборудования на новое такого же типа принимается только исходя из указанного критерия.

Введем обозначения: P - покупательная цена оборудования плюс затраты на его установку и запуск в эксплуатацию, C_j - ожидаемые затраты на эксплуатацию в течение j-го периода, S (j) - ожидаемая продажная стоимость оборудования после j периодов эксплуатации за вычетом расходов на демонтаж (если оборудование списывается, то S (j)) можно положить равным 0, а расходы на демонтаж отнести за счет установки нового оборудования).

Пусть ξ - возраст (выраженный в числе периодов) оборудования, а F (ξ) - ожидаемые затраты за все будущее время эксплуатации при условии, что в текущем и будущем ?периодах принимаются оптимальные решения о замене. величина F (ξ) нам, конечно, не известна, однако мы можем к определить затраты в следующем за ξ-м периоде:

- если принимается решение о продолжении эксплуатации старого оборудования;

- если покупается новое оборудование.

Требование минимизации ожидаемых затрат, очевидно, приводит нас к условию

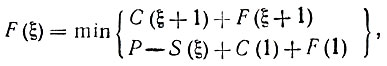
(3.74)

определяющему момент, когда выгоднее заменить оборудование; если верхнее выражение меньше нижнего, то оборудование менять не надо, если наоборот, то следует заменить, Уравнение, в состав которого одна и та же функция входит при разных значениях аргумента, называется функциональным.

Подобным же образом решается задача в том случае, когда критерием замены является требование получения максимального дохода в течение n-летнего периода эксплуатации, т. е. когда известно, что оставшееся время процесса составляет k лет (k<n). Обозначим N (ξ) - чистый доход от эксплуатации оборудования в течение периода от момента ξ до (ξ + 1), Φ_k (ξ) - чистый доход для процесса в k лет при условии, что оборудованию уже ξ лет (также при проведении оптимальной политики замены). Запишем сразу получающиеся соотношения:

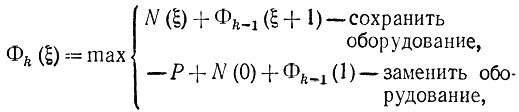
(3.75)

Здесь мы для простоты считали, что после решения о замене оборудование списывается.

Уравнения вида (3.74), (3.75) обычно оказывается трудно решать аналитически, однако не представляет очень большого труда решить их численно на ЭВМ. Пример программы для решения уравнений вида (3.75) приведен в работе [12].