§ 4. Модификация метода для случая непрерывности переменных, выпуклости или вогнутости функции цели

Вычислительный метод динамического программирования может быть применен также при решении задач с непрерывными переменными x_j. Посмотрим, к чему приведет отбрасывание требования целочисленности x_j, a_j и b в задаче (3.1).

Формально ничто не мешает начать решение этой задачи точно так же, как и в случае целочисленных переменных. Ври этом, как показано выше, следует определить последовательность функций F_k (ξ) (3.11). Теперь, однако, x_k меняется до ξ/a_k, а не до [ξ/a_k] и, вообще говоря, может принимать любые значения в интервале 0≤x_k≤b/a_k. По-скольку в любом таком интервале содержится бесконечное Множество чисел, то, как правило, функцию F_k (ξ) можно найти только приближенно. Выше (гл. II, §5) мы уже Встречались с методом приближенного определения макси-шума непрерывной функции. Этот метод можно применять и в данном случае.

Рассмотрим задачу определения F_k (ξ) при фиксированном ξ:

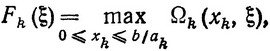
где

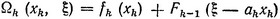
и считается, что F_k-1 (ξ) уже определена ранее. Функция Ω_k (x_k, ξ) также определена для всех x_k из интервала 0≤x_k≤b/a_k, и ее можно, например, изобразить в виде некоторой кривой аналогично тому, как это сделано на рис. 2.4. Для того чтобы определить значение 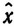_k (ξ), при котором Ω_k (x_k, ξ) достигает своего максимального значения, необходимо найти все относительные максимумы Ω_k и затем Убрать значения x_k, при которых Ω_k имеет абсолютный Максимум. Поскольку в отличие от случая, рассмотренного в гл. II, § 5, мы имеем здесь задачу только с одним переменным x_k, для приближенного определения максимума можно воспользоваться так называемым методом сеток, т. е. вычислять значения Ω_k при фиксированных и равноотстоящих значениях x_k из интервала 0≤x_k≤b/a_k. Повторяя процесс уменьшения шага сетки необходимое число раз в случае непрерывной функции Ω_k, всегда можно получить желаемую точность определения 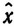_k (ξ) и F_k (ξ). Конечно, при этом объем вычислений будет значительным. Поэтому в отличие от других методов вычислительный метод динамического программирования более подходит для задач с целочисленными (дискретными) переменными.

Процесс определения 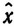_k и F_k (ξ) может быть существенно упрощен, если f_j (x_j) являются выпуклыми или вогнутыми функциями. Сначала рассмотрим случай, когда f_j (x_j) являются выпуклыми функциями (определение выпуклости и вогнутости функций см. гл. II, § 3). Покажем,что при этом F_k (ξ) также являются выпуклыми функциями ξ.

Прежде всего покажем, что если f₁ (x₁) является выпуклой функцией, то и F₁ (ξ) также является выпуклой функцией. Напомним, что для этого мы должны показать справедливость неравенства

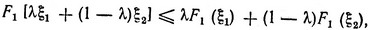
где λ - некоторое число (0≤λ≤1) и использовано представление ξ = λξ₁ + (1 - λ)ξ₂. Для простоты записи предположим, что все a_j = 1. Тогда можем написать:

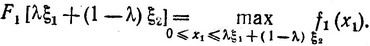
Разобьем x₁ также на два слагаемых следующим образом:

где λ - то же самое число, которое использовано в представлении ξ. Тогда при отыскании максимума изменение x₁ между 0 и λξ₁ + (1 - λ)ξ₂ можно производить путем независимого изменения x'₁ и x"₁ соответственно в пределах 0≤x"₁≤ξ₁ и 0≤x"₁≤ξ₂ Поэтому выражение (3.17) можно переписать в виде

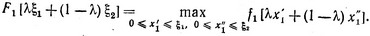
(3.18)

Однако вследствие выпуклости функции f₁ (x₁) мы имеем право написать:

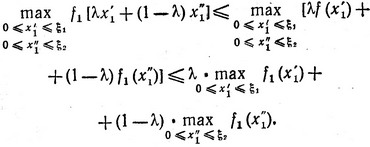
(3.19)

Если теперь в (3.19) обозначить

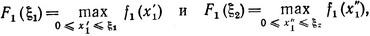
то в силу (3.18) можем переписать (3.19) в виде неравенства

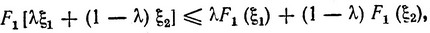
(3.20)

что и требовалось доказать. Следовательно, F₁ (ξ) также является выпуклой функцией.

Допустим теперь, что, проводя аналогичные рассуждения, доказали выпуклость функции F_k-1 (ξ). Докажем, что F_k(ξ) (3.11) также выпуклая функция.

Действительно, так как F_k-1 (ξ) - выпуклая функция по предположению при любом ξ, то F_k-1 (ξ-a_kx_k) также выпуклая функция от x_k и ξ. Функция f_k(x_k) - выпуклая по определению. Таким образом,

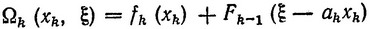
есть также выпуклая функция от x_k и ξ. Поступая так же как при доказательстве выпуклости F₁ (ξ), запишем:

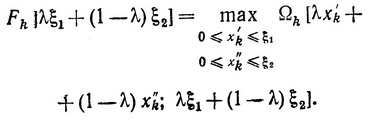
(3.21)

Из выпуклости Ω_k (x_k, ξ) следует:

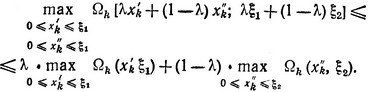
(3.22)

Опять поступая аналогично тому, как при получении неравенства (3.20), и учитывая (3.21), перепишем (3.22) в виде

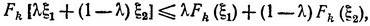
(3.23)

откуда следует выпуклость F_k (ξ). Таким образом, можно утверждать, что из выпуклости функций f_j (x_j) следует выпуклость всех функций F_k (ξ).

Аналогично можно показать, что из вогнутости функций f_j (x_j) следует вогнутость всех функций F_k (ξ).

После того как мы убедились, что при наличии выпуклости f_j (x_j) все функции Ω_k (x_k, ξ) также являются выпуклыми, можно воспользоваться доказанным в § 3 гл. II свойством выпуклых функций и утверждать, что максимум функций Ω_k (x_k, ξ) на интервале 0≤x_k≤ξ (ξ - заданное число) достигается в одной из крайних точек этого интервала, т. е.

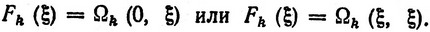
Ясно, что это приводит к существенному упрощению процесса определения 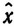_k (ξ) и F_k (ξ), о котором говорилось выше, поскольку необходимо только выбрать наибольшую из этих двух величин. При этом, однако, может случиться, что при x_k = 0 и x_k = 1 максимумы совпадают. Если Ω_k не зависит от x_k, то максимум достигается в любой внутренней точке интервала 0≤x_k≤ξ.

В случае вогнутости облегчение вычислений не так значительно. Единственно, чем можно воспользоваться - это тем обстоятельством, что любой относительный максимум вогнутой функции является также ее абсолютным максимумом. Поэтому упрощение вычислений сводится к тому, что представляется возможным вначале использовать метод сеток с довольно большим шагом. При достижении относительного максимума дальнейшие вычисления могут проводиться в окрестности этого максимума с помощью сеток с более мелким шагом. Зачастую этот прием позволяет существенно снизить вычислительные трудности.

заказать кредитную карту