§ 2. Понятие многошагового процесса

Во многих случаях понятие многошагового процесса представляется интуитивно ясным. Хорошо известен, естественно, многоэтапный процесс хозяйственного планирования, когда деятельность некоторого предприятия, системы предприятий, отрасли и т. д. планируется на некоторый отрезок времени, состоящий из нескольких периодов или хозяйственных лет, причем в конце соответствующего периода подводится оценка деятельности и, возможно, производится корректировка распределения средств на следующий период. Момент времени, в который принимается решение об очередном изменении переменных величин (управлений), часто именуется шагом.

Поясним математическую запись многошагового процесса с помощью примера. Для этого рассмотрим одну из самых простых задач распределения ресурсов.

Пусть задано некоторое количество ресурсов (средств) b, которое следует распределить между двумя отраслями производства. Известно из прежней деятельности этих отраслей, что количество средств x₁ вложенное в первую отрасль, за один год приносит доход f (x₁), и при этом средства расходуются так, что к концу года остается лишь количество, равное αx₁ (0<α<1). Соответственно во вторую отрасль можно вложить y₁ ≤ b - x₁ средств, которые принесут доход φ (y₁) и при этом уменьшатся до величины βy₁ (0≤β<1). Этот процесс продолжается в течение n лет, причем по истечении каждого года оставшиеся средства заново распределяются между отраслями и вкладываются в производство. Новых средств при этом не поступает. Необходимо в данных условиях найти такой способ управления ресурсами, при котором суммарный доход за период n лет окажется максимальным.

Общий доход двух отраслей за первый год составляет

доход за j-й год

Полный доход, очевидно, равен:

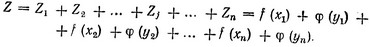
Таким образом, значение избранного критерия (общего дохода) получается простым суммированием частных значений этого критерия, достигнутых на отдельных шагах многошагового процесса Функция Z (x_i, y_i) есть функция цели, максимальное значение которой необходимо найти в ходе решения задачи.

Ограничениями нашей задачи являются условия на количество средств, вкладываемых в течение каждого года. Эти условия можно записать следующим образом:

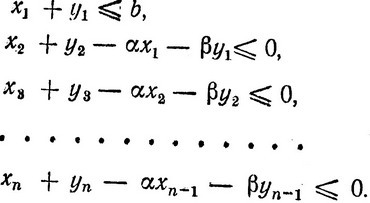
Суммируя эти неравенства, получаем иное ограничение на переменные задачи:

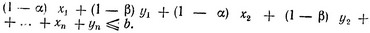
Конечно, то, что в приведенном выше примере требовалось распределить средства только между двумя отраслями производства, не является принципиальным. В общем случае можно говорить о любом числе отраслей и любом числе шагов. Поэтому, изменив обозначения, можно сформулировать задачу распределения в общем виде следующим образом:

найти

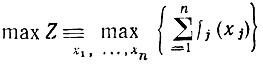
при ограничении

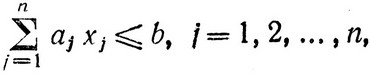
(3.1)

все

Если, кроме того, мы потребуем дополнительно, чтобы все x_j были целыми, то ни один из методов, описанных ранее, вообще говоря, не может быть использован для получения точного оптимального решения этой целочисленной задачи с сепарабельной функцией цели и только одним ограничением. Можно было бы предполагать сначала величины x_j непрерывными, т. е. отказаться от требования целочисленности, а затем округлить полученное решение до целых величин. В том случае, когда значения x_j>>1, такой подход обычно вполне допустим. Однако этот метод не может быть использован, если оптимальное значение x_j жало и особенно если f_о (x_j) не являются вогнутыми функциями, поскольку в последнем случае возможно наличие локальных максимумов.

Рассмотрим вычислительный метод, позволяющий найти оптимальное решение задачи (3.1), причем если это решение не единственное, то метод позволяет найти все оптимальные решения этой задачи.