§ 3. Максимум и минимум выпуклых и вогнутых функций

В задачах выпуклого программирования приходится иметь дело с так называемыми выпуклыми и вогнутыми функциями. Функция f (X), заданная на выпуклом множестве, содержащем граничные точки, называется выпуклой, если для любых двух точек X₁ и X₂ из этого множества и любого λ такого, что 0≤λ≤1, справедливо неравенство

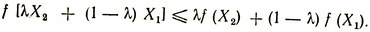
(2.4)

Функция, для которой знак неравенства изменен на обратный, называется вогнутой. Если f (X) - выпуклая функция, то - а (X) - вогнутая функция, и наоборот. Функции, для которых справедливы строгие неравенства вида (2.4), называются строго выпуклыми или строго вогнутыми.

Гиперповерхность z = f (X) является выпуклой, если отрезок, соединяющий любые две ее точки, лежит на самой поверхности или выше ее. Выпуклая функция одной переменной изображена на рис. 2.1. Геометрическое построение, представленное на этом рисунке, иллюстрирует неравенство (2.4).

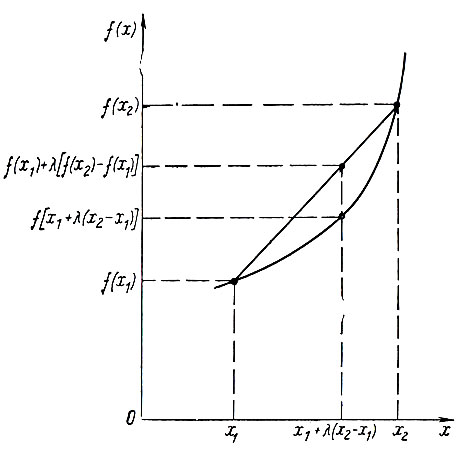
Рис. 2.1

Если же отрезок, соединяющий любые две точки гиперповерхности z = f (X), лежит на поверхности или ниже ее, то такая гиперповерхность называется вогнутой. На рис. 2.2 изображена вогнутая функция одной переменной.

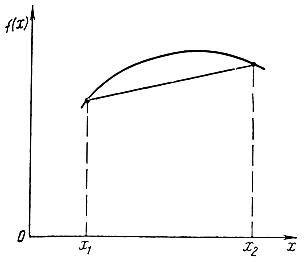
Рис. 2.2

Сумма выпуклых (вогнутых) функций также является выпуклой (вогнутой) функцией. В общем случае функция может быть выпуклой на некотором интервале и вогнутой на следующем интервале. Так, функция, изображенная на Рис. 2.3, не является ни вогнутой, ни выпуклой, так как на интервале (x₁, x₂) она обладает свойством выпуклости и свойством вогнутости на интервале (x₂, x₃).

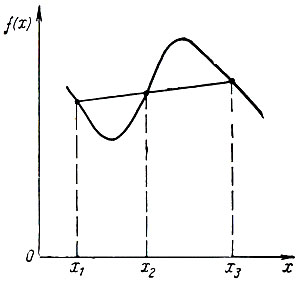
Рис. 2.3

Только линейная функция f = cx является одновременно и выпуклой, и вогнутой на всем множестве ее определения, так как для любых двух точек из этого множества x₁ и x₂ и любого λ (см. гл. I, § 3) имеет место равенство

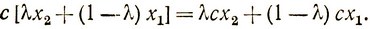
Приведем без доказательств (которые можно найти, например, в работе [8]) основные свойства выпуклых (вогнутых) функций.

1. Наиболее важным свойством строго выпуклых (вогнутых) функций является то, что их относительный минимум (максимум) совпадает с их абсолютным минимумом (максимумом) на заданном выпуклом множестве М, т. е. у этих функций имеется только один минимум (максимум).

2. Если выпуклая (вогнутая) функция достигает абсолютного минимума (максимума) в двух различных точках множества М, то она достигает этого минимума (максимума) также и в бесконечном числе точек этого множества.

3. Для выпуклой функции справедливо неравенство

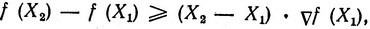
(2.5)

а для вогнутой функции - неравенство

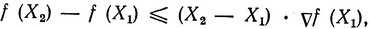
где (X₂ - X₁) есть n-мерный вектор, проведенный из точки X₁ в точку X₂, и символом ∇f(X₁) обозначен градиент функции f в точке X₁, являющийся n-мерным вектором с компонентами ^∂f/_∂xj.

Напомним, что векторами называются величины, которые характеризуются не только числовыми значениями, но и заданным направлением. Для определения направления используется набор единичных векторов e_j, направленных вдоль координатных осей соответствующих переменных. Положение любой точки X в n-мерном пространстве можно задать с помощью радиуса-вектора

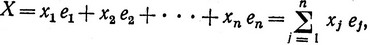
(2.6)

проведенного из начала координат в эту точку X (x₁, x₂, ..., x_n).

Единичные векторы e_j можно рассматривать как отрезки единичной длины с началом в любой точке x_j и концом в точке x_j+1.

Компонентами вектора ∇f являются частные производные, т. е.

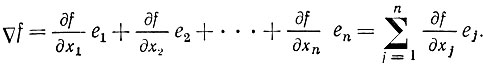
(2.7)

Вектор градиента (2.7) всегда направлен по нормали к поверхности f (X) = const, и длина его обратно пропорциональна расстоянию между этими поверхностями, т. е. там, где функция f (X) меняется быстрее, градиент увеличивается, и наоборот. Таким образом, величина градиента определяет скорость изменения функции при движении по направлению вектора ∇f, которое является направлением скорейшего изменения функции f. Отметим, что произведение двух векторов вида

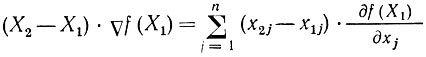
(2.8)

называется скалярным произведением этих векторов.

4. Минимум (максимум) непрерывной выпуклой (вогнутой) функции достигается на границе выпуклого множества, если ∇f≠0 нигде внутри этой области.

5. Максимум (минимум) выпуклой (вогнутой) функции либо достигается в одной или нескольких граничных точках выпуклого множества, либо достигается сразу во всех внутренних точках этого множества.

Существует достаточно общий метод решения задач выпуклого программирования, называемый методом наискорейшего спуска (подъема). Однако поскольку решение задач этим методом требует обычно весьма длительных вычислений, то, как и в линейном программировании, зачастую оказывается выгодным использовать более простые методы решения, разработанные применительно к некоторым видам задач. Примерами таких задач могут служить задачи с сепарабельными функциями и задачи с линейными ограничениями и выпуклыми (вогнутыми) функциями цели. Поэтому начнем рассмотрение методов решения задач выпуклого программирования с изложения методов решения этих двух задач, причем уже на этих примерах мы встретимся с элементами решения, которые в дальнейшем будут играть важную роль в методах наискорейшего спуска (подъема) или, как их еще часто называют, градиентных методах.