12.3. Конкуренция против сговора: дилемма заключенного

Равновесие Курно - это некооперативное равновесие: каждая фирма принимает решения, которые дают наибольшие возможные прибыли при данных действиях своих конкурентов. Как мы видели, итоговые прибыли, получаемые каждой фирмой, выше, чем они были бы при идеальной конкуренции, но ниже, чем если бы фирмы договорились друг с другом.

Сговор, однако, явление незаконное, и большинство руководителей предпочитают держаться подальше от тюрьмы или уплаты суровых штрафов. Но если кооперация может привести к более высоким прибылям, почему фирмы не сотрудничают без явного сговора? В частности, если вы и ваш конкурент можете вычислить максимизирующую прибыль цену, на которую вы согласились бы, если бы между вами существовал договор, почему бы не установить эту цену в надежде, что конкурент сделает то же самое? Если ваш конкурент сделает то же самое, вы оба получите больший доход.

Проблема заключается в том, что ваш конкурент может не выбрать установленные цены на договорном уровне. Фактически наиболее вероятно, что он не установит ее на договорном уровне. Почему? Потому что вашему конкуренту выгоднее установить цену Курно, даже если он знает, что вы собираетесь установить цену на договорном уровне.

Чтобы понять это, рассмотрим следующий пример с конкуренцией цен. Постоянные издержки каждой фирмы равны 20 долл., переменные издержки равны 0, и спрос на продукцию фирм определяют такими правилами:

Спрос фирмы 1: Q₁ = 12 - 2P₁ + Р₂. (12.3)

Спрос фирмы 2: Q₂ = 12 - 2Р₂ + Р₁. (12.4)

При равновесии Курно каждая фирма назначает цену в 4 долл. и зарабатывает прибыль в 12 долл., тогда как если фирмы договорятся между собой, они назначат цену в 6 долл. и получат прибыль в 16 долл. Теперь предположим, что фирмы не договорились, но фирма 1 назначает договорную цену в 6 долл., надеясь, что фирма 2 сделает то же самое. Если фирма 2 поступает точно так же, она получит прибыль в 16 долл. Но что будет, если она назначит вместо этого цену в 4 долл.? Тогда фирма 2 получит прибыль π₂ = P₂Q₂ - 20 = (4) X [12 - (2) (4) + 6] - 20 = 20 долл. Фирма 1, с другой стороны, получит прибыль π₁ = P₁Q₁ - 20 = (6) [12 - - (2) (6) + 4] - 20 = 4 долл.

Поэтому если фирма 1 назначает цену в 6 долл., а фирма 2 - только в 4 долл., прибыль фирмы 2 возрастет до 20 долл. за счет прибыли фирмы 1, у которой прибыль упадет до 4 долл. Очевидно, что фирма 2 выиграет, назначая цену только в 4 долл.

В табл. 12.2 сведены результаты различных возможных решений по ценообразованию. Решая, какую цену установить, две фирмы играют в некооперативную игру - каждая фирма самостоятельно решает, как ей лучше поступить, принимая в расчет своего конкурента. Табл. 12.2 называют платежной матрицей для этой игры, так как она показывает прибыль каждой фирмы, если известны ее решение и решение ее конкурента. Например, верхний левый угол платежной матрицы говорит нам, что, если обе фирмы назначат цену 4 долл., каждая фирма получит прибыль 12 долл. Верхний правый угол показывает, что, если фирма 1 назначает цену в 4 долл., а фирма 2 - в 6 долл., фирма 1 получает прибыль в 20 долл., а фирма 2 - в 4 долл.

Таблица 12.2. Платежная матрица для игры по прогнозированию цен

Данная платежная матрица может прояснить ответ на первоначальный вопрос: почему фирмы не действуют сообща и тем самым не получают более высокие прибыли, даже если они и имеют возможность договориться? В данном случае договор означает, что обе фирмы назначат цену в 6 долл. вместо 4 долл. и получат при этом прибыль 16 долл. вместо 12 долл. Проблема заключается в том, что каждая фирма всегда старается выиграть, назначая цену в 4 долл., независимо от того, как поступает ее конкурент. Как показывает платежная матрица, если фирма 2 назначает цену 4 долл., фирма 1 выигрывает, назначая цену 4 долл. А если фирма 2 назначает цену 6 долл., фирма 1 все равно выигрывает, назначая цену 4 долл. Аналогичным образом фирма 2 всегда будет в выигрыше, назначая цену 4 долл., независимо от того, как поступает фирма 1. В итоге пока две фирмы не могут подписать договорные обязательства и сообща назначить цену 6 долл., ни одна фирма не может ожидать, что ее конкурент назначит цену в 6 долл., - обе остановятся на цене 4 долл.

Классический пример теории игр, называемый дилеммой заключенных, иллюстрирует проблему, с которой сталкиваются олигопольные фирмы. Он заключается в следующем: двух заключенных обвинили в совместном совершении преступления. Они находятся в отдельных тюремных камерах и не могут поддерживать связь друг с другом. Каждого просили признаться в совершении преступления. Если оба заключенных сознаются, каждый получит срок заключения в 5 лет. Если никто не признается, судебное преследование будет трудно довести до конца, и поэтому заключенные могут получить двухгодичный срок наказания. С другой стороны, если один заключенный сознается, а другой нет, тот, кто признается, получит один год заключения, а другой сядет в тюрьму на десять лет. Если бы вы были одним из заключенных, сознались бы вы или нет?

Матрица табл. 12.3 сводит вместе возможные результаты (запись в нижнем правом углу матрицы означает двухгодичный приговор каждому заключенному). Перед этими заключенными стоит дилемма. Если бы они могли договориться о том, чтобы не признаваться (в форме обязательства), тогда каждый пошел бы в тюрьму только на два года. Но они лишены возможности говорить друг с другом, и даже если бы такая возможность существовала, могут ли они доверять друг другу? Если заключенный А не признается, он рискует, что этим воспользуется его бывший сообщник. Помимо всего прочего, что бы ни делал заключенный А, заключенный В за счет Признания выигрывает. Точно так же заключенный А всегда выигрывает благодаря признанию, и поэтому заключенному В надо беспокоиться о том, что если он не признается, то утратит преимущество. Следовательно, вероятнее всего, признаются оба заключенных и пойдут в тюрьму на пять лет.

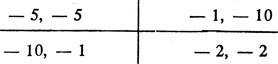
Tаблица 12.3. Расчетная матрица для дилеммы заключенных

Олигопольные фирмы часто оказываются на месте заключенных в дилемме. Они должны решить, следует ли им агрессивно конкурировать, пытаясь захватить большую долю рынка за счет конкурента, или "сотрудничать" и конкурировать более пассивно, сосуществуя со своим конкурентом и довольствуясь имеющейся долей, а может быть, даже тайно сговариваясь с ним. Если фирмы пассивно конкурируют, устанавливая высокие цены и ограничивая объем производства, они получат более высокие прибыли, чем при агрессивной конкуренции.

Подобно нашим заключенным, однако, у каждой фирмы есть стимул стать "штрейкбрехером" и сбить цены своим конкурентам, зная, что конкуренты стремятся к тому же. Как бы ни было желательно сотрудничество, каждая фирма беспокоится (и не без оснований), что, если она будет конкурировать пассивно, ее конкурент может конкурировать агрессивно, захватывая львиную долю на рынке. Для случая, показанного в табл. 12.2, обе фирмы будут в лучшем положении, "сотрудничая" и назначая высокую цену. Но фирмы стоят перед дилеммой заключенных, когда ни одна фирма не может ни доверять другой, ни ожидать, что ее конкурент назначит более высокую цену.

дебетовые карты